|
|
Лабораторная работа №2.1.2. Соударение шаровЦель работы: Экспериментальное и теоретическое нахождение значения импульса шаров до и после столкновения, коэффициента восстановления кинетической энергии, средней силы соударения двух шаров. Проверка закона сохранения импульса. Проверка закона сохранения механической энергии для упругих столкновений. Оборудование:установка «Соударение шаров» ФМ 17,состоящая из: основания 1, стойки 2, в верхней части которой устанавливается кронштейн верхний 3, предназначенный для подвески шаров; корпуса, предназначенного для крепления шкалы 4 угловых перемещений; электромагнита 5, предназначенного для фиксации исходного положения одного из шаров 6; узлов регулировки, обеспечивающие прямой центральный удар шаров; нити 7 для подвески металлических шаров; провода для обеспечения электрического контакта шаров с клеммами 8. Для пуска шара и подсчета времени до соударения служит блок управления 9. Металлические шары 6 выполнены из алюминия, латуни и стали. Масса шаров: латунь 110,00±0,03 г; сталь 117,90±0,03 г; алюминий 40,70±0,03 г. Краткая теория. При соударение шаров силы взаимодействия довольно резко изменяются с расстоянием между центрами масс, весь процесс взаимодействия протекает в очень малом пространстве и в очень короткий промежуток времени. Такое взаимодействие называют ударом. Различают два вида ударов: если тела являются абсолютно упругими, то удар называют абсолютно упругим. Если же тела абсолютно неупругие, то удар абсолютно неупругий. В данной лабораторной работе мы будем рассматривать только центральный удар, то есть удар, который происходит по линии, соединяющий центы шаров.
Рассмотрим задачу о ударе неупругих шаров количественно. Будем считать, что на них ни какие третьи тела не действуют. Тогда шары образуют замкнутую систему, в которой можно применить законы сохранения энергии и импульса. Однако силы действующие на них не консервативны. Поэтому к системе применим закон сохранения энергии:
где А- работа не упругих (консервативных) сил; E и E′ – полная энергия двух шаров соответственно до и после удара, состоящая из кинетической энергии обоих шаров и потенциальной энергии их взаимодействия между собой:
Так как до и после удара шары не взаимодействуют, то
Или Где Для определения конечной скорости шаров
Так как удар центральный, то все векторы скоростей лежат на одной прямой. Принимая эту прямую за ость X и проецируя уравнение (5) на эту ось, получим скалярное уравнение:
Из этого видно, что если шары до удара двигались в одну сторону, то после удара они будут двигаться в ту же сторону. Если же шары до удара двигались навстречу друг другу то после удара они будут двигаться в ту сторону, куда двигался шар, имеющий больший импульс. Поставим v′ из (6), в равенство (4):
Таким образом, работа внутренних неконсервативных сил при деформации шаров пропорциональна квадрату относительной скорости шаров. Абсолютно упругий удар протекает в два этапа. Первый этап – От начала соприкосновения шаров до выравнивания скоростей – протекает также, как и при абсолютно неупругом ударе, с той лишь разницей, что силы взаимодействия ( как силы упругости) зависят только от величины деформации и не зависят от скорости её изменения. Пока скорости шаров не сравнялись деформация будет нарастать и силы взаимодействия, замедляющие один шар и ускоряющие другой. В момент, когда скорости шаров сравняются, силы взаимодействия будут наибольшими, с этого момента начинается второй этап упругого удара: деформированные тела действуют друг на друга в том же направлении, в каком они действовали до выравнивания скоростей. Поэтому то тело, которое замедлялось будет продолжать замедляться, а то которое ускорялось – ускоряться, до тех пор пока деформация не исчезнет. При восстановлении формы тел вся потенциальная энергия вновь переходит в кинетическую энергию шаров, т. о. при абсолютно упругом ударе тела не изменяют своей внутренней энергии. Будем считать, что два соударяющихся шара образуют замкнутую систему, в которой силы являются консервативными. В таком случаи работа этих сил приводит к увеличению потенциальной энергии взаимодействующих тел. Закон сохранения энергии запишется следующим образом:
где
Решим систему уравнений (9) и (10) относительно 1 v′ и 2 v′. Для этого перепишем её в следующем виде:
Поделим первое уравнение на второе:
Решая систему из уравнения (11) и второго уравнения (10), получим:
Здесь скорости имеют положительный знак, если они совпадают с положительным направлением оси, и отрицательный – в противном случаи. Установка «Соударение шаров» ФМ 17: устройство и принцип работы:
Практическая часть Подготовка прибора к работе Перед началом выполнения работы необходимо проверить является удар шаров центральным, для этого нужно отклонить первый шар (меньшей массы) на некоторый угол и нажать клавишу Пуск. Плоскости траекторий движения шаров после столкновения должны совпадать с плоскостью движения первого шара до столкновения. Центра масс шаров в момент соударения должны находится на одной горизонтальной линии. Если этого не наблюдается, то необходимо выполнить следующие действия: 1. С помощью винтов 2 добиться вертикального положения колонны 3 (рис. 1). 2. Изменяя длину нити подвеса одного из шаров необходимо добиться того, что центры масс шаров находились на одной горизонтальной линии. При соприкосновении шаров нити должны быть вертикальны. Это достигается перемещением винтов 7 (см. рис. 1). 3. Необходимо добиться того, чтобы плоскости траекторий движения шаров после соударения совпадали с плоскостью траектории первого шара до столкновения. Это достигается с помощью винтов 8 и 10. 4. Отпустить гайки 20, угловые шкалы 15,16 установить таким образом, чтобы указатели углов в момент, когда шары занимают положение покоя, показывали на шкалах ноль. Затянуть гайки 20. Задание 1.Определить время соударения шаров. 1. Вставит алюминиевые шары в скобы подвеса. 2. Включить установку 3. Отвести первый шар на угол 4. Нажать кнопу «ПУСК». При этом произойдет удар шаров. 5. По таймеру определить время соударения шаров. 6. Занести результаты в таблицу. 7. Сделать 10 измерений, результаты занести в таблицу 8. Рассчитать среднее время соударения 9. Сделать вывод о зависимости времени соударения от механических свойств материалов соударяющихся тел.
Задание 2. Определить коэффициенты восстановления скорости и энергии для случая упругого удара шаров. 1. В скобы вставить алюминиевые, стальные или латунные шары (по указанию преподавателя). Материал шаров:
2. Отвести первый шар к электромагниту и записать угол бросания 3. Нажать кнопу «ПУСК». При этом произойдет удар шаров. 4. При помощи шкал визуально определить углы отскока шаров 5. Результаты занести в таблицу.
6. Произвести 10 измерений результаты занести в таблицу. 7. По полученным результатам произвести расчет оставшихся величин по формулам. Скорости шаров до и после удара можно вычислить следующим образом:
где l - расстояние от точки подвеса до центра тяжести шаров;
Коэффициент восстановления скорости можно определить по формуле:
Коэффициент восстановления энергии можно определить по формуле :
Потерю энергии при частично упругом соударении можно вычислить по формуле:
8. Произвести расчеты средних значений всех величин. 9.Произвести расчет погрешностей по формулам:
10. Записать получившиеся результаты с учётом погрешности в стандартом виде. Задание 3. Проверка закона сохранения импульса при неупругом центральном ударе. Определение коэффициента восстановления кинетической энергии. Для изучения неупругого удара берутся два стальных шара, но на одном из них в месте, где происходит удар, прикрепляют кусочек пластилина. Шар, который отклоняют к электромагниту, считается первым.
Таблица №1
1. Получите у преподавателя начальное значение угла отклонения первого шара 2. Установите электромагнит так, чтобы угол отклонения первого шара соответствовал заданному значению 3. Отклоните первый шар на заданный угол, нажмите клавишу <ПУСК> и произведите отсчёт угла отклонения второго шара 4. Масса шаров 5. По формуле 6. По формуле 7. По формуле 8. По формуле 9. По формуле 10. По формуле 11. По формуле 12. По формуле 13. По формуле 14. Запишите ответ для импульса системы после столкновения в виде 15. Найдите отношение
Задание 4. Проверка закона сохранения импульса и механической энергии при упругом центральном ударе. Определение силы взаимодействия шаров при столкновении. Для изучения упругого удара берутся два стальных шара. Шар, который отклоняют к электромагниту, считается первым. Таблица №2.
1. Получите у преподавателя начальное значение угла отклонения первого шара 2. Установите электромагнит так, чтобы угол отклонения первого шара соответствовал заданному значению 3. Отклоните первый шар на заданный угол, нажмите на клавишу <ПУСК> и произведите отсчёт углов отклонения первого шара 4. Массы шаров 5. По формуле 6. По формуле 7. По формуле 8. по Формуле 9. По формуле 10. По формуле 11. По формуле 12. По формуле 13. По формуле 14. По формуле 15. Запишите ответ для импульса системы после столкновения в виде: 16. Запишите интервал для кинетической энергии системы после столкновения в виде: 17. Найдите отношение проекции импульса системы после упругого удара 18. Найдите отношение кинетической энергии системы после упругого удара 19. Сравните полученное значение величины силы взаимодействия Контрольные вопросы: 1. Охарактеризуйте виды ударов, укажите какие законы при ударе выполняются? 2. Механическая система. Закон изменения импульса, закон сохранения импульса. Понятие о замкнутой механической системе. Когда для незамкнутой механической системы можно применить закон сохранения импульса? 3. Определите скорости тел одинаковой массы после удара в следующих случаях: 1) первое тело движется второе покоиться. 2) оба тела движутся в одном направлении. 3) оба тела движутся в противоположном направлении. 4. Определите величину изменения импульса равномерно вращающейся по окружности точки массой m. Через полтора, через четверть периода. 5. Сформируйте закон сохранения механической энергии, в каких случаях он не выполняется. 6. Запишите формулы для определения коэффициентов восстановления скорости и энергии, объясните физический смысл. 7. От чего зависит величина потери энергии при частично упругом ударе? 8. Импульс тела и импульс силы, виды механической энергии. Механическая работа силы.
|
|
 Рассмотрим абсолютно неупругий удар. Этот удар можно наблюдать на двух свинцовых или восковых шарах, подвешенных на нити одинаковой длинны. Процесс соударения протекает следующим образом. Как только шары А и В придут в соприкосновение, начнется их деформация, в результате которой возникнут силы сопротивления (вязкое трение), затормаживающие шар А и ускоряющие шар В. Так как эти силы пропорциональны скорости изменения деформации (т. е. относительной скорости движения шаров), то по мере уменьшения относительной скорости они убывают и обращаются в нуль, как только скорости шаров выровняться. С этого момента шары, «слившись», движутся вместе.
Рассмотрим абсолютно неупругий удар. Этот удар можно наблюдать на двух свинцовых или восковых шарах, подвешенных на нити одинаковой длинны. Процесс соударения протекает следующим образом. Как только шары А и В придут в соприкосновение, начнется их деформация, в результате которой возникнут силы сопротивления (вязкое трение), затормаживающие шар А и ускоряющие шар В. Так как эти силы пропорциональны скорости изменения деформации (т. е. относительной скорости движения шаров), то по мере уменьшения относительной скорости они убывают и обращаются в нуль, как только скорости шаров выровняться. С этого момента шары, «слившись», движутся вместе. (1)
(1)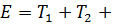 U,
U,  (2)
(2) и соотношение (1) принимает вид:
и соотношение (1) принимает вид: (3)
(3) (4)
(4) массы шаров;
массы шаров;  - их скорости до соударения; v′ - скорость шаров после удара. Поскольку A<0, то равенство (3) показывает, что кинетическая энергия системы уменьшилась. Деформация и нагрев шаров произошли за счет убыли кинетической энергии.
- их скорости до соударения; v′ - скорость шаров после удара. Поскольку A<0, то равенство (3) показывает, что кинетическая энергия системы уменьшилась. Деформация и нагрев шаров произошли за счет убыли кинетической энергии. следует воспользоваться законом сохранения импульса
следует воспользоваться законом сохранения импульса (5)
(5) (6)
(6)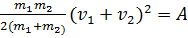 (7)
(7)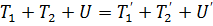
 - кинетические энергии шаров в произвольный момент времени t (в процессе удара), а U - потенциальная энергия системы в тот же момент.
- кинетические энергии шаров в произвольный момент времени t (в процессе удара), а U - потенциальная энергия системы в тот же момент.  − значение тех же величин в другой момент времени t′. Если момент времени t соответствует началу соударения, то
− значение тех же величин в другой момент времени t′. Если момент времени t соответствует началу соударения, то  ; если t′ соответствует концу соударения, то
; если t′ соответствует концу соударения, то  Запишем законы сохранения энергии и импульса для двух этих моментов времени:
Запишем законы сохранения энергии и импульса для двух этих моментов времени: (8)
(8) (9)
(9) (10)
(10)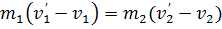
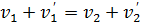 (11)
(11) ,
,  (12)
(12) 1 Установка "Соударение шаров" представлена на рисунке и состоит из: основание 1, стойку 2, в верхней части которой устанавливается кронштейн верхний 3, предназначенный для подвески шаров; корпус, предназначенный для крепления шкалы 4 угловых перемещений; электромагнит 5, предназначенный для фиксации исходного положения одного из шаров 6; узлы регулировки, обеспечивающие прямой центральный удар шаров; нити 7 для подвески металлических шаров; провода для обеспечения электрического контакта шаров с клеммами 8. Для пуска шара и подсчета времени до соударения служит блок управления 9. Металлические шары 6 выполнены из алюминия, латуни и стали.
1 Установка "Соударение шаров" представлена на рисунке и состоит из: основание 1, стойку 2, в верхней части которой устанавливается кронштейн верхний 3, предназначенный для подвески шаров; корпус, предназначенный для крепления шкалы 4 угловых перемещений; электромагнит 5, предназначенный для фиксации исходного положения одного из шаров 6; узлы регулировки, обеспечивающие прямой центральный удар шаров; нити 7 для подвески металлических шаров; провода для обеспечения электрического контакта шаров с клеммами 8. Для пуска шара и подсчета времени до соударения служит блок управления 9. Металлические шары 6 выполнены из алюминия, латуни и стали. и зафиксировать его с помощью электромагнита.
и зафиксировать его с помощью электромагнита.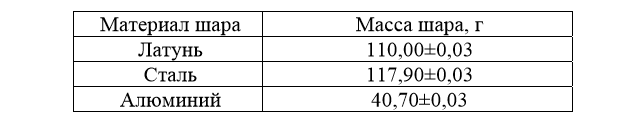
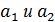
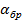
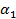


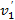



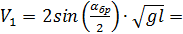
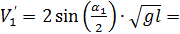
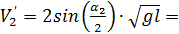
 - угол отскока правого шара, градусов;
- угол отскока правого шара, градусов;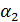 - угол отскока левого шара, градусов.
- угол отскока левого шара, градусов.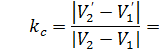
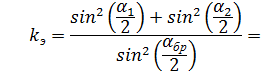
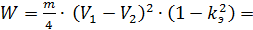
 =
= =
= =
= =
=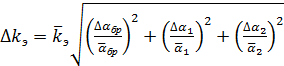 =
= =
=
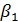


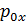

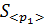


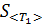

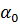 и запишите его в таблицу №1.
и запишите его в таблицу №1.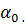
 . Опыт повторите 5 раз. Полученные значения угла отклонения
. Опыт повторите 5 раз. Полученные значения угла отклонения 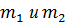 указанны на установке.
указанны на установке.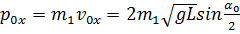 найдите импульс первого шара до столкновения и запишите результат в табл. №1.
найдите импульс первого шара до столкновения и запишите результат в табл. №1.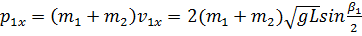 найдите 5 значений импульса системы шаров после столкновения и запишите результат в табл. №1.
найдите 5 значений импульса системы шаров после столкновения и запишите результат в табл. №1. найдите среднее значение импульса системы после столкновения.
найдите среднее значение импульса системы после столкновения. найдите дисперсию среднего значения импульса системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения
найдите дисперсию среднего значения импульса системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения 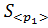 импульса системы после столкновения. Полученное значение
импульса системы после столкновения. Полученное значение  занесите в таблицу №1.
занесите в таблицу №1. найдите начальное значение кинетической энергии первого шара до столкновения
найдите начальное значение кинетической энергии первого шара до столкновения  , и занесите его в таблицу №1.
, и занесите его в таблицу №1. найдите пять значений кинетической энергии системы шаров после столкновения
найдите пять значений кинетической энергии системы шаров после столкновения  , и занесите их в табл. №1.
, и занесите их в табл. №1. 5 найдите среднее значение кинетической энергии системы после столкновения.
5 найдите среднее значение кинетической энергии системы после столкновения.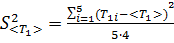 найти дисперсию среднего значения кинетической энергии системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения
найти дисперсию среднего значения кинетической энергии системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения 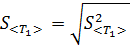 кинетической энергии системы после столкновения. Полученное значение
кинетической энергии системы после столкновения. Полученное значение 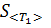 занесите в табл. №2.
занесите в табл. №2.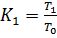 найдите коэффициент восстановления кинетической энергии
найдите коэффициент восстановления кинетической энергии 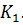 По полученному значению коэффициента восстановления кинетической энергии сделайте вывод о сохранении энергии системы во время столкновения.
По полученному значению коэффициента восстановления кинетической энергии сделайте вывод о сохранении энергии системы во время столкновения.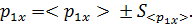
 проекции импульса системы после неупругого удара
проекции импульса системы после неупругого удара 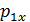 к начальному значению проекции импульса системы до удара
к начальному значению проекции импульса системы до удара  . По полученному значению отношения проекции импульсов до и после столкновения сделайте вывод о сохранении импульса системы во время столкновения.
. По полученному значению отношения проекции импульсов до и после столкновения сделайте вывод о сохранении импульса системы во время столкновения.




 и второго шара
и второго шара 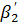 и времени соударения шаров
и времени соударения шаров  . Опыт повторите 5 раз. Полученные значения углов отклонения и времени соударения запишите в табл. №2.
. Опыт повторите 5 раз. Полученные значения углов отклонения и времени соударения запишите в табл. №2.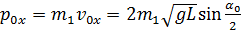 найдите импульс первого шара до столкновения и запишите результат в таблицу №2.
найдите импульс первого шара до столкновения и запишите результат в таблицу №2.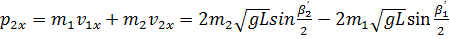 найдите 3 значений импульса системы шаров после столкновения и запишите результат в табл. №2.
найдите 3 значений импульса системы шаров после столкновения и запишите результат в табл. №2. найдите среднее значение импульса системы после столкновения.
найдите среднее значение импульса системы после столкновения. найти дисперсию среднего значения импульса системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения
найти дисперсию среднего значения импульса системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения 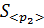 импульса системы после столкновения. Полученное значение
импульса системы после столкновения. Полученное значение  найдите пять значений кинетической энергии системы шаров после столкновения
найдите пять значений кинетической энергии системы шаров после столкновения  , и результаты занесите в табл. № 2.
, и результаты занесите в табл. № 2. найдите среднее значение кинетической энергии системы после столкновения
найдите среднее значение кинетической энергии системы после столкновения найти дисперсию среднего значения кинетической энергии системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения
найти дисперсию среднего значения кинетической энергии системы шаров после столкновения. Найдите среднеквадратичное отклонение среднего значения  кинетической энергии системы после столкновения. Полученное значение
кинетической энергии системы после столкновения. Полученное значение  занесите в табл. №2.
занесите в табл. №2. найдите коэффициент восстановления кинетической энергии
найдите коэффициент восстановления кинетической энергии  .
.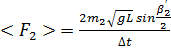 найдите среднее значение силы взаимодействия
найдите среднее значение силы взаимодействия  и результат занесите в таблицу №2.
и результат занесите в таблицу №2.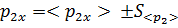 .
. .
. к начальному значению проекции импульса до удара
к начальному значению проекции импульса до удара  . По полученному значению отношения проекции импульсов до и после столкновения сделайте вывод о сохранении импульса системы во время столкновения.
. По полученному значению отношения проекции импульсов до и после столкновения сделайте вывод о сохранении импульса системы во время столкновения.