|
|
Лабораторная работа №2.3.4. Изучение вынужденных колебаний в LCR-контуреЦель работы:Изучение установившейся реакции колебательной системы (LCR- контура) на непрерывное внешнее воздействие, изменяющееся во времени по гармоническому закону; исследование резонанса. Приборы и оборудование: модуль «ФПЭ-11/10», магазины емкостей «МЕ» и сопротивлений «МС»; постоянное оборудование: генератор ГЗ-112, осциллограф С1-93 (С1-83), два цифровых вольтметра, комплект соединительных кабелей. СОДЕРЖАНИЕ РАБОТЫ Теоретическое описание вынужденного колебательного процесса. В данной работе мы продолжается изучение колебательных процессов в одиночном LCR-контуре, имеющем собственную частоту
Рис. 1.Электрический колебательный контур под воздействием внешней ЭДС
Условимся считать положительным ток, заряжающий конденсатор (рис. 1). По закону Ома
где I — сила тока в контуре, Заряд на конденсаторе q, напряжение на нем Uc, ток в контуре I и ЭДС самоиндукции
Подставив выражение (2) в формулу (1) и произведя преобразования, получим уравнение
где Общее решение полученного линейного дифференциального уравнения второго порядка дает закон изменения заряда во времени. Из теории дифференциальных уравнений известно, что общее решение равно сумме частного решения уравнения (3) и решения однородного уравнения
Решение уравнения (4) описывает процесс свободных затухающих колебаний в контуре
где Частное решение уравнения (15.3) имеет вид
где амплитуда колебаний заряда равна
а фазовый сдвиг α находится из выражения
При начальном возбуждении контура в нем возникает сложный переходный колебательный процесс, представляющий суперпозицию затухающих колебаний на частоте Продифференцировав выражение (6), найдем силу тока в контуре при установившихся колебаниях:
Обозначив
где
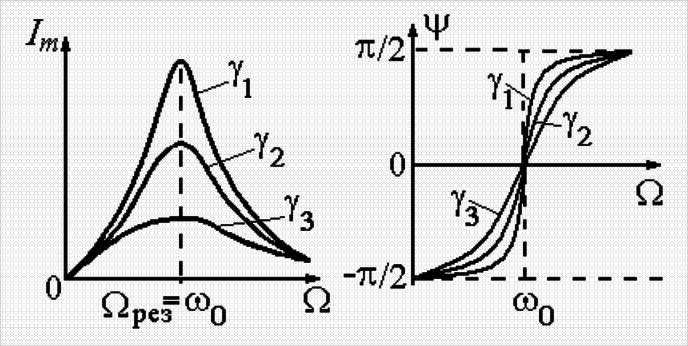
Рис. 2.Зависимость амплитуды тока и сдвига фаз от частоты при различных затуханиях
Зависимость амплитуды вынужденных колебаний силы тока I и сдвига фаз Как видно из выражений (10) и (11) для тока резонанс достигается при
Другими словами, при резонансе колебания тока происходят с максимальной амплитудой на частоте, равной собственной частоте контура и в фазе с приложенной ЭДС. Резонансную частоту для заряда q и напряжения на конденсаторе Ucможно получить, исследовав на экстремум функцию (7) или выражение для амплитуды напряжения на конденсаторе
Легко показать, что
При малом затухании
Выражение (13) совпадает с формулой для добротности Q, введенной ранее для характеристики затухания колебательного контура. Здесь выявляется другой физический смысл добротности: величина Q показывает, во сколько раз напряжение на конденсаторе при резонансе превышает величину воздействующей на контур внешней ЭДС. Добротность Q характеризует также такое свойство колебательного контура, как избирательность. Это свойство связано с остротой резонансных кривых и оценивается шириной резонансных кривых на уровне половинной мощности колебаний
Величина
Рис. 3.Определение полосы пропускания контура МЕТОДИКА ИЗМЕРЕНИЙ 1. Схема установки для изучения резонанса в последовательном LCR-контуре приведена на рис. 4. Катушка индуктивности L и резистор R]находятся в модуле ФПЭ-11, емкость контура и сопротивление устанавливаются магазинами МЕ и МС. Внешняя ЭДС частоты
Рис. 4.Схема для измерения амплитудно-частотной (резонансной) и фазово-частотной характеристик контура: МС — магазин сопротивлений, МЕ — магазин емкостей
На вход осциллографа подается напряжение с небольшого резистора R1пропорциональное силе тока I в контуре. Изменяя частоту генератора, исследуют зависимости I = I(v) при различных сопротивлениях R. 2. Измерение сдвига фаз
Рис. 5.Определение полосы пропускания контура
Измерив линейный сдвиг фазы
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Задание 1.Измерение амплитудно-частотной характеристики контура (резонансной кривой)для тока 1.Соберите схему в соответствии с рис. 4. 2.Установите емкость контура 3.Используя приблизительное значение индуктивности L≈100 мГн, рассчитайте ориентировочно собственную частоту контура по формуле 4.Подготовьте приборы к работе. Осциллограф включите в режим работы с внутренней временной разверткой и внешней синхронизацией. Для одновременного наблюдения осциллограмм I(t) и х ( t) установите род работы «→→». Напряжение с генератора (ЭДС) установите ≈3 В на частоте v=1кГц (размах на экране ~ 4 В). 5. Получите устойчивое изображение сигналов ЭДС и тока и измерьте амплитуды Примечание. Если имеется возможность измерять оба напряжения вольтметрами, то в таблицу заносите показания вольтметров, а осциллограммы используйте только для визуального наблюдения. В дальнейшем поддерживайте величину Проделайте измерения при других частотах в диапазоне 1…10 кГц. Частоту изменяйте с шагом 1–2 кГц, а вблизи резонанса с шагом 0,2 кГц. Результаты заносите в таблицу 1.
Таблица 1.
7.Рассчитайте для всех частот амплитуду тока в контуре. Результаты также занесите в таблицу 1 (ток в мА). 8. Повторите измерения по пп. 5, 6, 7 при величинах сопротивления магазина R = 200 Ом и R = 600 Ом. 9. Постройте графики Im = Im(v) для R=0, 200 и 600 Ом на одном чертеже. 10. По графикам для R=0 и R=600 Ом определите ширину резонансных кривых Задание 2.Определение фазово-частотных характеристик контура. Установите сопротивление R = 0, емкость С = 2 Установите такую длительность развертки, чтобы на экране наблюдались синусоиды сигналов I(t) и х(t)в пределах одного периода Т Измерьте сдвиг осциллограмм Сопоставьте измеренные значения сдвига фаз с теоретически ожидаемыми величинами (см. рис. 2 и формулу (11)). КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что такое резонанс? 2. Особенности явления резонанса в последовательной цепи. Условия возникновения резонанса в ней. 3. Особенности явления резонанса в параллельной цепи. Условия возникновения резонанса в ней. 4. Что такое добротность контура? На что она влияет и от чего зависит. 5. Вывести формулу вынужденных колебаний в контуре.
ОПТИКА |
|
 , подвергнув его воздействию непрерывно действующей внешней гармонической ческой ЭДС
, подвергнув его воздействию непрерывно действующей внешней гармонической ческой ЭДС  . Генератор частоты
. Генератор частоты  включим последовательно в контур (рис. 1). Будем считать, что мгновенные значения токов и напряжений удовлетворяют законам, установленным для цепей постоянного тока. Такие токи называются квазистационарными.
включим последовательно в контур (рис. 1). Будем считать, что мгновенные значения токов и напряжений удовлетворяют законам, установленным для цепей постоянного тока. Такие токи называются квазистационарными.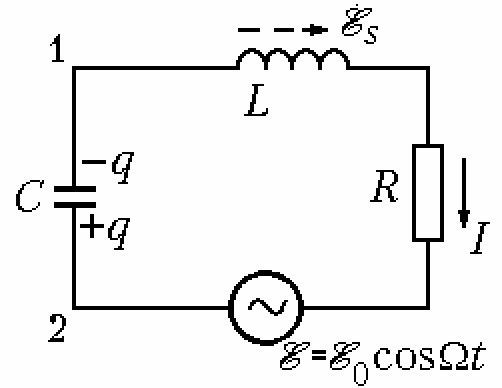
 можно написать
можно написать , (1)
, (1) –напряжение на конденсаторе,
–напряжение на конденсаторе,  — ЭДС самоиндукции.
— ЭДС самоиндукции. в индуктивности L связаны соотношениями:
в индуктивности L связаны соотношениями:

 (2)
(2) (3)
(3)
 – коэффициент затухания и
– коэффициент затухания и  – собственная частота контура.
– собственная частота контура. (4)
(4) (5)
(5) .
. (6)
(6) (7)
(7) (8)
(8) и незатухающих колебаний на частоте внешней ЭДС
и незатухающих колебаний на частоте внешней ЭДС  . По прошествию достаточного времени колебания на частоте
. По прошествию достаточного времени колебания на частоте  исчезают, и будут происходить только вынужденные колебания на частоте
исчезают, и будут происходить только вынужденные колебания на частоте  , описываемые функцией (6). Аналогично происходят и колебания напряжения на конденсаторе. В дальнейшем будем рассматривать только этот установившийся колебательный процесс.
, описываемые функцией (6). Аналогично происходят и колебания напряжения на конденсаторе. В дальнейшем будем рассматривать только этот установившийся колебательный процесс.

 – сдвиг по фазе между током и приложенной ЭДС и подставив значения
– сдвиг по фазе между током и приложенной ЭДС и подставив значения  и
и  , получаем
, получаем (9)
(9) (10)
(10) (11)
(11)
 от частоты внешней ЭДС
от частоты внешней ЭДС  приведена на рис. 2. Из графика видно, что амплитуда тока резко возрастает при приближении частоты
приведена на рис. 2. Из графика видно, что амплитуда тока резко возрастает при приближении частоты  внешней ЭДС к некоторой характеристической частоте контура. Это явление называется резонансом, а соответствующая частота, при которой достигается максимум – резонансной частотой
внешней ЭДС к некоторой характеристической частоте контура. Это явление называется резонансом, а соответствующая частота, при которой достигается максимум – резонансной частотой  .
. , откуда
, откуда 

 (12)
(12) резонансную частоту для напряжения можно считать равной
резонансную частоту для напряжения можно считать равной  , а для амплитуды напряжения при резонансе получается, Отношение амплитуды напряжения на конденсаторе при резонансе к амплитуде внешней ЭДС будет в этом случае равно
, а для амплитуды напряжения при резонансе получается, Отношение амплитуды напряжения на конденсаторе при резонансе к амплитуде внешней ЭДС будет в этом случае равно (13)
(13) или для тока и напряжения на уровне
или для тока и напряжения на уровне  . Можно показать, что при малом затухании
. Можно показать, что при малом затухании  отношение этой ширины к резонансной частоте обратно величине добротности контура
отношение этой ширины к резонансной частоте обратно величине добротности контура (14)
(14) называется полосой пропускания контура (рис. 3).
называется полосой пропускания контура (рис. 3).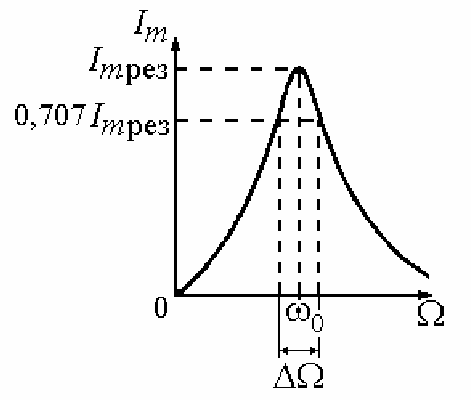
 задается генератором ГЗ-112
задается генератором ГЗ-112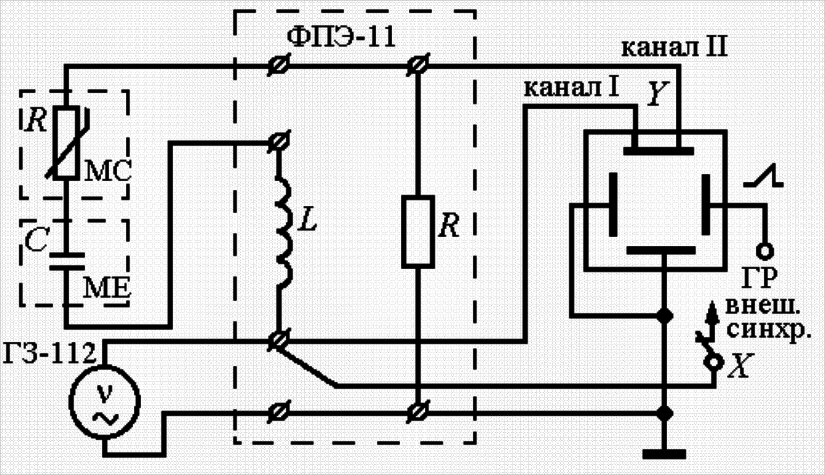
 между током I и внешней ЭДС х ( t) может быть выполнено при одновременном наблюдении осциллограмм I(t) и х(t). Подав напряжения с резистора R1и генератора в каналы YI и YII, получим сдвинутые на интервал времени
между током I и внешней ЭДС х ( t) может быть выполнено при одновременном наблюдении осциллограмм I(t) и х(t). Подав напряжения с резистора R1и генератора в каналы YI и YII, получим сдвинутые на интервал времени  осциллограммы соответствующих напряжений. Удобно при этом синхронизировать развертку напряжением x(t) (рис. 5).
осциллограммы соответствующих напряжений. Удобно при этом синхронизировать развертку напряжением x(t) (рис. 5).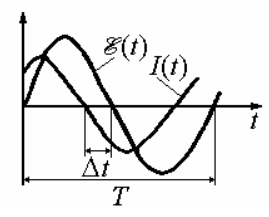
 (в единицах длины или времени) на экране осциллографа и длину периода Т, найдем фазовый угол по формуле
(в единицах длины или времени) на экране осциллографа и длину периода Т, найдем фазовый угол по формуле (5)
(5) .
. мкФ и внешнее сопротивление магазина R = 0 (или 1 Ом).
мкФ и внешнее сопротивление магазина R = 0 (или 1 Ом).
 и
и  (или размахи
(или размахи  и
и  ) на экране. Занесите значения частоты, амплитуд и масштабных множителей каналов
) на экране. Занесите значения частоты, амплитуд и масштабных множителей каналов  ,
, 
 неизменной.
неизменной. , дел
, дел
 , В/дел
, В/дел
 (см. рис. 3) и рассчитайте добротность контура по формуле (14).
(см. рис. 3) и рассчитайте добротность контура по формуле (14). 10–2мкФ.
10–2мкФ. относительно друг друга и период Т в делениях шкалы. Рассчитайте сдвиг фаз
относительно друг друга и период Т в делениях шкалы. Рассчитайте сдвиг фаз  между током и внешней ЭДС на некоторых частотах: резонансной
между током и внешней ЭДС на некоторых частотах: резонансной  ; на частотах по обе стороны от резонанса
; на частотах по обе стороны от резонанса  , соответствующих амплитуде
, соответствующих амплитуде  ; на частотах вдали от резонанса.
; на частотах вдали от резонанса.