|
|
Лабораторная работа №2.3.3. Исследование зависимости сопротивления металлов и полупроводников от температурыЦель работы: нахождение вида зависимости сопротивления образцов металла и полупроводника от температуры. Приборы и принадлежности: лабораторная установка ФПК-07, состоящая из измерительного устройства и электропечи с образцами.
Теория Все вещества обладают электропроводностью – способностью проводить электрический ток. Электрический ток – это направленное движение заряженных частиц. Для его существования необходимо наличие носителей тока, т.е. частиц, которые могли бы свободно перемещаться под действием электрического поля. В металлах носителями тока являются отрицательно заряженные свободные электроны. В жидкостях (электролитах) носители тока – ионы, имеющие как отрицательные, так и положительные заряды. В твердых полупроводниках и диэлектриках реальными частицами – носителями тока являются электроны, но для описания закономерностей их перемещения используется модель, учитывающая перемещение и вакантных связей электронов – положительно заряженных квазичастиц, «дырок». Вне зависимости от наличия электрического поля, все носители тока участвуют в тепловом движении со скоростями, имеющими очень большую величину. Однако в силу хаотичности теплового движения, среднее значение вектора скорости на протяжении любого конечного промежутка времени равно нулю. Поэтому, при отсутствии электрического поля, отсутствует и результирующее смещение носителей заряда. При наложении внешнего электрического поля с напряженностью Е, на носители тока с зарядом q начинает действовать сила. В результате на протяжении промежутка времени dt осуществляется упорядоченное перемещение (дрейф) носителей тока в направлении вектора E (для положительного заряда) с направленной (дрейфовой) скоростью, то есть возникает электрический ток. Легко получить связь силы тока I с величиной направленной скорости u для однородного проводника (рис. 1).
По определению, сила тока равна величине заряда, переносимого через поперечное сечение проводника в единицу времени. Как было упомянуто, тепловое движение не дает вклада в направленное перемещение носителей тока и это перемещение определяется исключительно скоростью дрейфа u. За время dt поверхность c площадью S пересекут все носители тока, находившиеся от нее на расстоянии u ⋅ dt , то есть, в объеме S ⋅ u ⋅ dt. Соответствующее количество частиц – носителей тока равно n ⋅ S ⋅ u ⋅ dt, где n – количество частиц в единице объема (концентрация носителей тока). Если q – заряд одной частицы, то величина перенесенного заряда – q ⋅ n ⋅ S ⋅ u ⋅ dt, и сила тока: I = q ⋅ n ⋅ u ⋅ S. Векторную величину называют плотностью тока. Во всех точках однородного проводника сила тока I = j ⋅ S. Соотношение (1) позволяет произвести оценку величины дрейфовой скорости u. В качестве примера, рассчитаем дрейфовую скорость свободных электронов в медном проводе. В меди концентрация свободных электронов равна концентрации атомов n , которую найдем, зная число молей вещества в проводе ν и постоянную Авогадро
Учтем, что ν=m/µ (где m – масса провода, µ=0,0635 кг/моль – молярная масса меди) и что отношение ρ=m/V – плотность меди, равная 8900 кг/м3. Тогда: Рассмотрим провод сечением S = 1 Окончательно, из соотношения (1) получаем:
То есть, величина скорости направленного дрейфа не превышает одного миллиметра в секунду, что несравнимо меньше, чем модуль скорости хаотического теплового движения ( В большинстве проводников при обычных условиях скорость дрейфа прямо пропорциональна величине напряженности электрического поля:
где коэффициент пропорциональности µ называют подвижностью носителей тока. В этих случаях пропорциональной напряженности поля
где Величину ρ = 1/ Соответственно: Соотношения (3) и (4) представляют собой дифференциальную (векторную) форму закона Ома. Напомним, что полное электрическое сопротивление R цилиндрического однородного проводника с длиной L и площадью поперечного сечения S равно Наилучшими проводниками тока являются металлы, обладающие малым удельным сопротивлением ( Изучение зависимости сопротивления металлов от температуры имеет важное значение для экспериментальной физики и техники. Большинство точных измерений температуры в настоящее время производится с помощью так называемых термометров сопротивления (терморезисторов). Они представляют собой проволочные резисторы, температурная зависимость которых тщательно проградуирована в специальных термостатах. Эти термометры точнее, удобнее в использовании и диапазон их сравнительно шире, чем у ртутных и других жидкостных термометров. Платиновые терморезисторы, например, применяются в диапазоне от –263 до + 1000°С. Точность таких термометров составляет несколько сотых долей градуса, а их сопротивление прямо пропорционально температуре (рис. 2).
Рис. 2. Зависимость сопротивления металлов от температуры
Для не слишком больших интервалов температуры (и не слишком низких температур) удельное сопротивление и других металлов удовлетворительно описывается линейной зависимостью
Здесь Естественно, так же зависит от температуры и сопротивление любого однородного металлического проводника (резистора), если он весь имеет эту температуру:
Для большинства чистых металлов температурный коэффициент сопротивления близок к величине, равной 1/273 ≈ 3,67· В 1900 году немецкий ученый П. Друде на основании гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории. Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла. Как ионы, образующие решетку, так и электроны участвуют в тепловом движении. Ионы совершают тепловые колебания вблизи положений равновесия – узлов кристаллической решетки. Свободные электроны движутся хаотично и при своем движении сталкиваются с ионами решетки. В результате таких столкновений устанавливается термодинамическое равновесие между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет выразить среднюю скорость теплового движения электронов с массой m
где k = 1,38⋅ В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Обозначим среднюю длину свободного пробега (среднее расстояние между соударениями) через λ, среднее время свободного пробега: τ =λ/<V>, где – <V> средний модуль скорости электрона (сумма <VT> и <u>). Так как <VT> >>> <u> , то можно считать, что <V> =<VT> и τ=λ / <VT> . Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью. В промежутке между соударениями на электрон с зарядом q = e = 1,6⋅
где τ – время свободного пробега (время между соударениями электрона с ионами). Среднее значение скорости дрейфа <u> равно половине максимального значения:
Окончательно, из формулы (2) можно получить теоретическое выражение для подвижности электронов в металле:
В классической электронной теории величину λ считают постоянной, которая определяется строением кристаллической решетки данного металла. Поэтому единственной переменной величиной в формуле (11) является Так как в металлах концентрация свободных электронов постоянна, то влияние температуры на удельную проводимость и удельное сопротивление целиком определяется изменениями µ(T):
По формуле (5), сопротивление однородного проводника (резистора):
где А – величина, постоянная для данного резистора. На первый взгляд, теоретически полученная пропорциональность
Если ограничиться первыми двумя членами разложения, то формула (15) преобразуется к виду, совпадающему с экспериментальной формулой (7):
где α* = 1/546 ≈ 1,8⋅ Рассмотрим далее механизмы собственной и примесной проводимости полупроводников. Особенности электропроводности полупроводников не могут быть объяснены в рамках классической модели идеального газа свободных электронов и необходимо использование квантовой статистики и зонной теории твердых тел. В полупроводниках имеются носители тока двух видов: отрицательно заряженные электроны и положительно заряженные дырки с одинаковыми по абсолютной величине зарядами e. Поэтому для полупроводников формула для плотности тока (3) принимает вид:
и удельная проводимость
где Рассмотрим особенности формирования носителей тока в чистых (беспримесных) полупроводниках 4-й группы (германий Ge, кремний Si). Между двумя атомами полупроводника имеет место ковалентная связь, осуществляемая парой электронов, принадлежащих обоим этим атомам. Если все ковалентные связи заполнены, то свободных электронов в кристалле нет и, следовательно, электропроводность такого кристалла будет равна нулю. На рис. 3 показана двумерная схема кристаллической решетки чистого кремния (Si). При T = 0°К свободных электронов в решетке нет, так как все валентные электроны участвуют в связях. Флуктуации теплового движения атомов при повышении температуры могут привести к разрыву ковалентных связей в некоторых местах кристалла и освобождению свободных электронов, которые теперь могут участвовать в проводимости. Следовательно, чтобы валентный электрон стал электроном проводимости, ему надо сообщить некоторую энергию активации (
Рис. 3. Двумерная схема кристаллической решетки чистого кремния (Si)
На рисунке хорошо видна схема образования носителей тока в чистом полупроводнике. Темные кружки – свободные электроны. Светлые кружки и пунктирные линии изображают незаполненные ковалентные связи – дырки. После ухода электрона со связи, она остаётся незаполненной (изображена пунктиром). В эту незаполненную связь могут перемещаться связанные электроны с соседних связей. Движение связанных электронов по вакантным незаполненным связям в некотором направлении эквивалентно движению положительно заряженных незаполненных связей в противоположном направлении. Таким образом, при разрыве ковалентных связей в полупроводнике возникают два механизма электропроводности: проводимость свободных электронов, движущихся против электрического поля, и проводимость валентных электронов по незаполненным связям, которую можно эквивалентно описать, как движение в направлении электрического поля положительно заряженных незаполненных связей, называемых дырками (светлые кружки на рис. 3). Очевидно, что в чистых полупроводниках концентрации электронов и дырок одинаковы:
В полупроводниках, как и в металлах, подвижность носителей тока зависит от температуры, однако зависимостью µ(Т) можно пренебречь по сравнению с более сильной зависимостью от температуры концентрации электронов и дырок n(Т), то есть, можно считать, что в полупроводниках µ ≈ const. Таким образом, если в металлах температурная зависимость сопротивления определяется изменением подвижности µ(Т) при n = const, то в полупроводниках подвижность практически не меняется, а на величину проводимости (и сопротивления) влияет только изменение концентрации носителей тока:
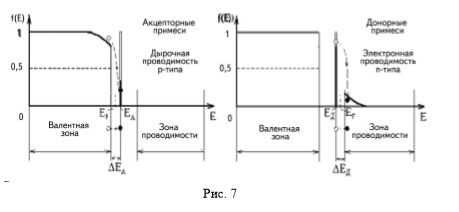
При объяснении зависимости n(Т) необходимо учитывать квантовые свойства электронов, в частности, то, что они обладают полу целым спином, то есть принадлежат к классу фермионов и их распределение по энергиям описывается функцией Ферми-Дирака:
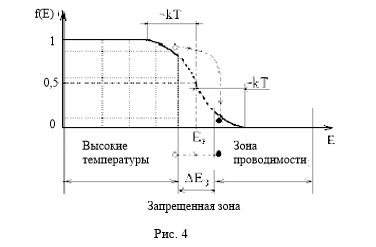
где В кристаллических твердых телах, из-за наличия периодической структуры кристаллической решетки, возможные энергетические состояния электронов образуют группы, называемые энергетическими зонами. Совокупность энергетических уровней связанных валентных электронов формирует валентную зону. Энергетические уровни свободных электронов формируют зону проводимости. В полупроводниках между верхней границей валентной зоны На рис. 4 приведена вероятность нахождения электронов в различных энергетических состояниях (распределение Ферми-Дирака) при Т>0. Видно, что в чистом полупроводнике уровень Ферми
Так как
Расчеты показывают, что такая же зависимость от температуры характерна и для концентрации свободных электронов:
где N(E) – распределение плотности энергетических состояний по энергиям; Как было упомянуто, в чистых полупроводниках уровень Ферми расположен вблизи середины запрещенной зоны и
Из формулы (20), температурная зависимость удельной электропроводности чистых полупроводников:
Соответственно, удельное сопротивление полупроводника ρ и полное сопротивление терморезистора R быстро убывают при увеличении температуры по экспоненциальному закону:
В формулах (23), (24) и (25) Из последней формулы видно, что между логарифмом сопротивления и величиной обратной температуры имеется линейная связь, где коэффициент пропорциональности определяется шириной запрещенной зоны:
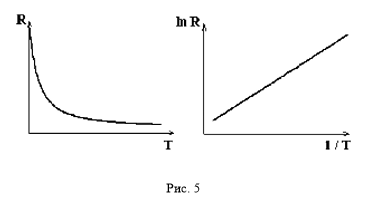
Характерные значения ширины запрещенной зоны в чистых полупроводниках при температуре 300 К – от нескольких десятых долей электрон-вольта до 1-3 электрон-вольт. Так, в одноэлементных полупроводниках IV группы: На рис. 5 показаны примерные графики зависимостей R(T) и lnR(1/T) для полупроводников с собственной проводимостью.
Рис. 5. Графики зависимостей R(T) и lnR(1/T) для полупроводников с собственной проводимостью
Введение в полупроводники незначительного количества примесей (≈ При замещении атома германия атомом примеси, имеющим три валентных электрона, (например, атомом индия In) одна валентная связь германия оказывается не заполненной электроном слева (рис. 6).
Рис 6. Примесная проводимость полупроводников
Электрон одной из соседних заполненных связей может перейти в незаполненную связь. Причем этот переход требует гораздо меньшей энергии активации Таким образом, введение трехвалентной примеси в решетку германия приводит к возникновению свободных уровней (дырок) вблизи верхней границы валентной зоны. Уровни, способные захватывать валентные электроны (и соответствующие примеси), называют акцепторными. При наличии акцепторных примесей не образуются свободные электроны и основными носителями тока являются дырки (обозначаемые сокращением p – от слова positive). Подобные примесные полупроводники называются полупроводниками p-типа. Уровень Ферми
Рис. 7. Уровень Ферми
Если в кристалл германия ввести пятивалентный атом примеси (например, мышьяк As), то пятый электрон мышьяка окажется слабо связанным с атомом (рис. 7, справа). Для того чтобы оторвать его от атома и превратить в свободный носитель тока, и в этом случае требуется значительно меньшее количество энергии В диапазоне низких температур сопротивление примесных полупроводников изменяется по закону:
В акцепторных полупроводниках энергия активации примеси
В диапазоне «высоких» температур происходит так называемое истощение примеси (при практически используемых концентрациях примесей в полупроводниковых устройствах, комнатные температуры уже являются «высокими»). В акцепторных полупроводниках все уровни примесей заполняются электронами из валентной зоны. В донорных полупроводниках все электроны с уровней примесей переходят в зону проводимости. При этих температурах основную роль приобретают переходы электронов из валентной зоны в зону проводимости (возникает собственная проводимость) и температурная зависимость сопротивления начинает изменяться по законам в формулах (24) и (25).
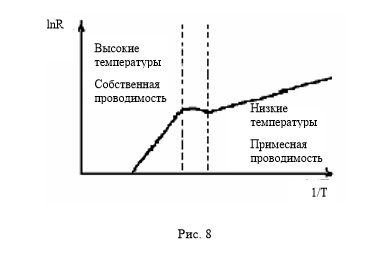
Рис. 8. Изменение характера проводимости примесных полупроводников в различных диапазонах температур
Диапазоны «низких» и «высоких» температур разделяет промежуточная область, где зависимость R(T) не описывается экспоненциальным законом. Изменение характера проводимости примесных полупроводников в различных диапазонах температур становится хорошо видным на графике lnR(1/T) – рис. 8. Промышленные полупроводниковые датчики температуры (термисторы) изготавливают из примесных полупроводников. Очень редко исходным материалом служит чистый германий или кремний. Часто используют легированные примесями полупроводники типа
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА Общий вид экспериментальной установки показан на рис.9. Установка состоит из двух блоков: А и Б. Внутри блока А расположена электрическая печь с датчиком температуры, используемая для нагрева исследуемых образцов и вентилятор, необходимый для быстрого охлаждения печи по окончании каждого цикла измерений.
Рис. 9. Общий вид экспериментальной установки.
На передней панели блока находится смотровое окно 1, позволяющее наблюдать образцы, установленные в печи. Поочередное подключение образцов к измерительной цепи производится с помощью переключателя «ОБРАЗЕЦ» 2. В двух крайний положениях «0» вход измерительной цепи закорочен. Для проведения измерений с образцом металла (меди) переключатель устанавливают в положение «1». Измерения с образцом полупроводника (термистора) проводят, устанавливая переключатель в положение «3». ВНИМАНИЕ. При установке переключателя в положение «2» к измерительной цепи подключен образец сплава с низким температурным коэффициентом сопротивления, который в данной лабораторной работе не используется. На передней панели блока «А» размещены также следующие органы управления и индикации: 3 – выключатель «СЕТЬ», предназначенный для включения и выключения служебных цепей блока «А». ВНИМАНИЕ. Для включения и выключения печи и вентилятора используются органы управления, расположенные в блоке «Б». При включенной печи внутри нее загорается лампа, хорошо видная сквозь смотровое окно 5. 4 – индикатор «СЕТЬ», загорающийся при включении выключателя «СЕТЬ». 5 – индикатор «ВЕНТ», загорающийся при включении вентилятора. В блоке Б расположены устройства управления печью и вентилятором, измерительное устройство, выполненное в виде конструктивно законченного изделия. В нем применена однокристальная микро-ЭВМ с соответствующими дополнительными устройствами, позволяющими производить измерение температуры образцов (температуры в электропечи), объекта исследования и сопротивление образцов в процессе нагрева, а также осуществлять функции управления установкой (включение-выключение электропечи и вентилятора, остановка индикации при снятии показаний с индикатора и т.п.). В состав измерительного устройства входят так же источники его питания и жидкокристаллический индикатор.
ВНИМАНИЕ. Выключатель блока «СЕТЬ» 6 расположен на его задней панели, слева. На передней панели блока «Б» расположены следующие органы управления и индикации: 7 – жидкокристаллический индикатор. В верхней строке индикатора высвечивается температура образца в градусах Цельсия – например: «t = 024 8 – кнопка включения/выключения печи «НАГРЕВ». Когда печь включена, то на индикаторе появляется служебное сообщение «Warm» и загорается лампа в смотровом окне блока «А». 9 – кнопка включения/выключения вентилятора «ВЕНТ.». Когда вентилятор включен, то на индикаторе появляется служебное сообщение «Cool» и становится слышен характерный шум работы вентилятора в блоке «А». 10 – кнопка остановки непрерывной индикации «СТОП ИНД.». Когда индикация остановлена, значения температуры и сопротивления перестают изменяться и на индикаторе появляется служебное сообщение «Fixed». ВНИМАНИЕ. В данной лабораторной работе функция остановки не используется. Если сообщение «Fixed» появилось в результате каких-либо случайных действий с кнопкой остановки, его необходимо сразу убрать с экрана путем повторного нажатия кнопки «СТОП ИНД.».
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Ознакомьтесь с органами управления блоков лабораторной установки 2. Включите питание блоков «А» и «Б» с помощью соответствующих выключателей «СЕТЬ». 3. Дайте схемам прогреться 3-5 минут. 4. Установите переключатель «ОБРАЗЕЦ» на блоке «А» в положение «1» (образец металла). 5. Включите печь нагревателя кнопкой «НАГРЕВ» на блоке «Б». Проверьте, появилось ли служебное сообщение «Warm» на индикаторе и загорелась ли лампа в смотровом окне блока «А». 6. Внимательно следите за изменениями температуры на индикаторе. При достижении температуры 40 ВНИМАНИЕ. При индикации одного и того же значения температуры, значения сопротивления на индикаторе могут изменяться. Для записи в таблицу выберите значение R, которое кажется Вам наиболее устойчивым при данной температуре. 7. Повторяйте измерения сопротивления металла через каждые 5 8. После проведения измерений при температуре 110 Таблица 1 |
|

 (1)
(1) =6,02 ⋅
=6,02 ⋅  :
: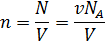
 .
. , по которому течет значительный ток силой I = 10 А, то есть плотность тока имеет величину j = I/S =
, по которому течет значительный ток силой I = 10 А, то есть плотность тока имеет величину j = I/S =  А/
А/  . Заряд электрона известен: q = e = 1,6⋅
. Заряд электрона известен: q = e = 1,6⋅ 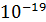 Кл.
Кл.
 м/с).
м/с).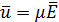 (2)
(2) (3)
(3) – удельная проводимость вещества.
– удельная проводимость вещества. =
=  называют удельным сопротивлением.
называют удельным сопротивлением. (4)
(4) (5)
(5) ÷
÷  ) Ом · м. Диэлектрики почти не проводят ток, их удельное сопротивление очень велико: (
) Ом · м. Диэлектрики почти не проводят ток, их удельное сопротивление очень велико: ( 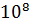 ÷
÷  ) Ом · м. Промежуточное положение по электропроводности занимают полупроводники. Их удельное сопротивление (
) Ом · м. Промежуточное положение по электропроводности занимают полупроводники. Их удельное сопротивление ( 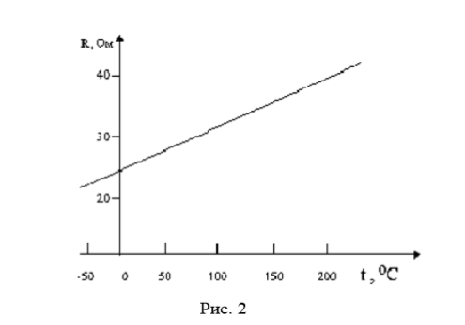
 (6)
(6) – удельное сопротивление при температуре 0°С; α – температурный коэффициент сопротивления; t – температура в градусах Цельсия.
– удельное сопротивление при температуре 0°С; α – температурный коэффициент сопротивления; t – температура в градусах Цельсия. (7)
(7) .
. кг по формулам молекулярно-кинетической теории:
кг по формулам молекулярно-кинетической теории: (8)
(8) Дж/К = 8,62⋅
Дж/К = 8,62⋅  эВ/К – постоянная Больцмана.
эВ/К – постоянная Больцмана.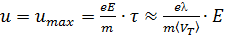 (9)
(9)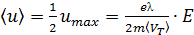 (10)
(10) (11)
(11) зависящая от температуры. Таким образом, классическая электронная теория предсказывает, что с увеличением температуры металла подвижность свободных электронов убывает в результате увеличения частоты соударений электронов с ионами кристаллической решетки:
зависящая от температуры. Таким образом, классическая электронная теория предсказывает, что с увеличением температуры металла подвижность свободных электронов убывает в результате увеличения частоты соударений электронов с ионами кристаллической решетки: 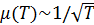 .
. (12)
(12) (13)
(13) (14)
(14) противоречит экспериментальной линейной зависимости сопротивления от температуры в формуле (7). Однако необходимо иметь в виду, что экспериментальную зависимость (7) обычно считают справедливой лишь в ограниченном интервале температур по шкале Цельсия (чаще всего, от 0 до 100
противоречит экспериментальной линейной зависимости сопротивления от температуры в формуле (7). Однако необходимо иметь в виду, что экспериментальную зависимость (7) обычно считают справедливой лишь в ограниченном интервале температур по шкале Цельсия (чаще всего, от 0 до 100  ). Перейдем и в формуле (14) от абсолютной температурной шкалы Т к шкале Цельсия t:
). Перейдем и в формуле (14) от абсолютной температурной шкалы Т к шкале Цельсия t: . (15)
. (15)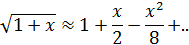
 (16)
(16) – в достаточно хорошем соответствии с экспериментальными значениями температурного коэффициента сопротивления для различных металлов. Таким образом, несмотря на то, что все допущения классической электронной теории являются весьма приближенными, эта теория качественно объясняет многие закономерности электрического тока в металлических проводниках. Однако следует иметь в виду, что в ряде вопросов наглядная классическая теория проводимости металлов не в состоянии объяснить все явления, связанные с прохождением тока через металлические проводники, в частности, она дает приближенную зависимость сопротивления R от температуры Т (о чем отмечалось выше), не объясняет, почему электроны не участвуют в аккумулировании теплоты, подводимой к металлу и т.д. Электрон в кристалле должен рассматриваться как волна (квантовая теория), и именно волновые свойства определяют его поведение. Дело в том, что в кристалле характерным размером является постоянная решетки d – величина порядка размера атома (
– в достаточно хорошем соответствии с экспериментальными значениями температурного коэффициента сопротивления для различных металлов. Таким образом, несмотря на то, что все допущения классической электронной теории являются весьма приближенными, эта теория качественно объясняет многие закономерности электрического тока в металлических проводниках. Однако следует иметь в виду, что в ряде вопросов наглядная классическая теория проводимости металлов не в состоянии объяснить все явления, связанные с прохождением тока через металлические проводники, в частности, она дает приближенную зависимость сопротивления R от температуры Т (о чем отмечалось выше), не объясняет, почему электроны не участвуют в аккумулировании теплоты, подводимой к металлу и т.д. Электрон в кристалле должен рассматриваться как волна (квантовая теория), и именно волновые свойства определяют его поведение. Дело в том, что в кристалле характерным размером является постоянная решетки d – величина порядка размера атома ( 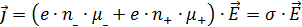 . (17)
. (17)  (18)
(18) концентрация и подвижность электронов;
концентрация и подвижность электронов;  концентрация и подвижность дырок.
концентрация и подвижность дырок. ), равную энергии разрыва ковалентной связи.
), равную энергии разрыва ковалентной связи.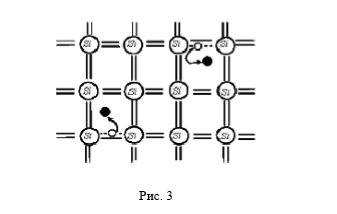
 Описанный тип проводимости полупроводников называют собственной проводимостью. В этом случае:
Описанный тип проводимости полупроводников называют собственной проводимостью. В этом случае: (19)
(19) (20)
(20) (21)
(21) – вероятность нахождения электрона в состоянии с энергией E; T – температура системы (по шкале Кельвина); k – постоянная Больцмана;
– вероятность нахождения электрона в состоянии с энергией E; T – температура системы (по шкале Кельвина); k – постоянная Больцмана;  – энергия уровня Ферми (это характеристическая энергия системы, ниже которой при T = 0 K все состояния заполнены, выше – пустые).
– энергия уровня Ферми (это характеристическая энергия системы, ниже которой при T = 0 K все состояния заполнены, выше – пустые). и нижней границей зоны проводимости
и нижней границей зоны проводимости  имеется интервал энергий
имеется интервал энергий 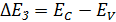 , внутри которого отсутствуют возможные энергетические состояния электронов – так называемая запрещенная зона.
, внутри которого отсутствуют возможные энергетические состояния электронов – так называемая запрещенная зона.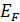 расположен вблизи середины запрещенной зоны (в связи с отсутствием разрешенных состояний в этой области энергий, функция
расположен вблизи середины запрещенной зоны (в связи с отсутствием разрешенных состояний в этой области энергий, функция  изображена пунктирной линией). Схематически показано, что увеличение вероятности заполнения энергетических уровней в зоне проводимости
изображена пунктирной линией). Схематически показано, что увеличение вероятности заполнения энергетических уровней в зоне проводимости  0), то есть, возникновение свободных электронов, происходит за счет уменьшения вероятности заполнения энергетических уровней в валентной зоне (
0), то есть, возникновение свободных электронов, происходит за счет уменьшения вероятности заполнения энергетических уровней в валентной зоне (  ).
).
 .Тогда распределение по энергиям (21) для свободных электронов принимает вид:
.Тогда распределение по энергиям (21) для свободных электронов принимает вид: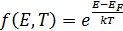 (22)
(22)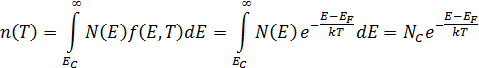
 – нижняя граница зоны проводимости;
– нижняя граница зоны проводимости;  – эффективная плотность состояний в зоне проводимости (число состояний в единичном интервале энергий) – величина, постоянная для данного материала.
– эффективная плотность состояний в зоне проводимости (число состояний в единичном интервале энергий) – величина, постоянная для данного материала. . Поэтому зависимость концентрации свободных электронов (и концентрации дырок) от температуры определяется шириной запрещенной зоны:
. Поэтому зависимость концентрации свободных электронов (и концентрации дырок) от температуры определяется шириной запрещенной зоны:
 (23)
(23) (24)
(24) (25)
(25) и
и  – постоянные величины.
– постоянные величины. (26)
(26) ≈ 0,67 эВ (Ge) и
≈ 0,67 эВ (Ge) и  ≈ 1,12 эВ (Si). В двухэлементных полупроводниках типа
≈ 1,12 эВ (Si). В двухэлементных полупроводниках типа  :
:  :
: 
 %) приводит к значительному увеличению электропроводности. Проводимость, обусловленная наличием примесей в полупроводнике, называется примесной. Рассмотрим основные особенности примесной проводимости.
%) приводит к значительному увеличению электропроводности. Проводимость, обусловленная наличием примесей в полупроводнике, называется примесной. Рассмотрим основные особенности примесной проводимости.
 по сравнению с энергией
по сравнению с энергией  .
.
 , чем энергия
, чем энергия 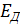 .
. (27)
(27) (28)
(28) , в донорных полупроводниках:
, в донорных полупроводниках: 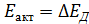
 . Распространены также термисторы на основе полупроводников сложного состава – смесей оксидов переходных металлов.
. Распространены также термисторы на основе полупроводников сложного состава – смесей оксидов переходных металлов.
 ». В нижней строке индикатора высвечивается сопротивление образца (Ом) – например «R = 043,4 Om». В верхнем правом углу индикатора появляются служебные сообщения.
». В нижней строке индикатора высвечивается сопротивление образца (Ом) – например «R = 043,4 Om». В верхнем правом углу индикатора появляются служебные сообщения. С запишите соответствующее значение сопротивления металла в табл. 1.
С запишите соответствующее значение сопротивления металла в табл. 1. С, как в табл. 1.
С, как в табл. 1.