Определение фокусного расстояния линзы

1.3.1. Собирающая линза

Существует большое количество методов экспериментального определения фокусного расстояния линзы. Остановимся лишь на трех из них, применяемых при выполнении данной работы.

Метод I.Фокусное расстояние линзыFможно определить,исходя изформулы (1) для тонкой линзы: (3)

Расстояния a и b измеряются на установке, состоящей из собирающей линзы, источника света, объекта и экрана для наблюдения изображения. Так как на экране можно наблюдать только действительное изображение, то для собирающей линзы должно быть выполнено условие a>F (см. табл.1).

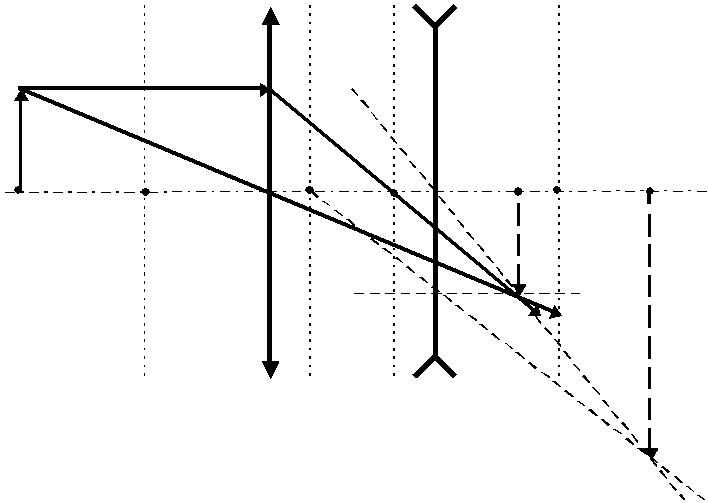
Рис. 5. Построение изображения для оптической системы, состоящей из собирающей и рассеивающей линз: A — мнимый источник, A — изображение, F —фокус линзы

Недостатком такого способа определения фокусного расстояния линзы является то, что на самом деле любая линза не является тонкой, и расстояния следует отсчитывать от соответствующих главных плоскостей линзы, определение которых довольно затруднительно.

Метод II.Если источник света и экран находятся на расстоянииL,болеечем в 4 раза превышающее F, то всегда найдутся два таких положения линзы с соответствующими расстояниями до объекта и изображения (a₁ , b₁ ) и (a₂ , b₂ ), при которых на экране будут наблюдаться четкие изображения. Так как

Обозначим через s расстояние, на которое следует переместить линзу для перехода от первого изображения ко второму:

s=a₂ - a₁ или s=b₁ - b₂

(пусть для определенности a₂>a₁). Тогда из соотношений

L=a₁ + b₁ = a₁ + s + b₂ = 2 × a₁ + s

и

L=a₂ + b₂ = b₁ + b₁ - s = 2 ×b₁ - s

следует, что

и .

Тогда из формулы тонкой линзы получим: (4).

Описанный способ определения фокусного расстояния линзы является наиболее общим и применимым как для тонких, так и для толстых линз, так как, в отличие от первого способа, измеряются не расстояния до линзы, а ее перемещение.

Метод III.Если при проведении измерений вторым способом уменьшатьрасстояние L между объектом и экраном, то оба положения линзы, дающие четкое изображение, будут сближаться, и при L = 4F сольются друг с другом. Найдя это положение, можно также найти фокусное расстояние:

Однако визуально различить случаи, когда при перемещении линзы будет наблюдаться только одно изображение или два близко расположенных изображения, довольно затруднительно, поэтому при измерениях, проводимых указанным способом, возможны существенные погрешности.

1.3.2. Рассеивающая линза

Из табл. 2 следует, что с помощью рассеивающей линзы действительное изображение можно получить только когда a<0 и |a|<|F|, т.е. источник света должен быть, во-первых, мнимым, и, во-вторых, находиться от линзы на расстоянии, меньшем ее фокусного расстояния. Добиться выполнения обоих условий можно, если перед рассеивающей линзой установить собирающую (рис. 5). Эта линза даст действительное изображение A¢B¢, которое станет «источником» света для рассеивающей линзы. Если установить рассеивающую линзу так, чтобы были выполнены вышеуказанные условия, то будет сформировано действительное изображение A¢¢B¢¢, которое можно наблюдать на экране. Измерив расстояния от рассеивающей линзы до точки B¢ (обозначим его a,при этом a<0)и до точки B¢¢(обозначим его b,при этом b>0),из формулытонкой линзы получим:

(6)

т.е. фокусное расстояние рассеивающей линзы отрицательно.

Аберрации оптических систем

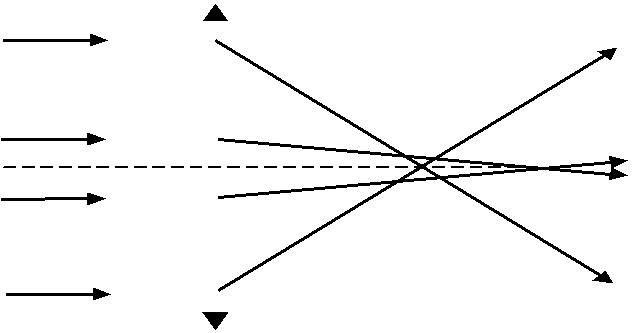
В реальных оптических системах получаемые изображения обычно не точно соответствуют источникам, не вполне отчетливы, оказываются окрашенными и т.п. Такие искажения называются геометрическими или лучевыми аберрациями оптической системы.Различают несколько видоваберраций:

1) астигматизм ¾прошедшая от точечного источника волна перестаетбыть сферической, т.е. изображение не является стигматичным, а представляет собой две взаимно перпендикулярные линии, расположенные в разных плоскостях на некотором расстоянии друг от друга;

2) кома ¾изображение точечного источника,расположенного не наглавной оптической оси системы, имеет вид неравномерно освещенного пятнышка, напоминающего комету;

3) сферическая аберрация ¾исходящие из точечного источника лучи,прошедшие вблизи главной оптической оси системы и прошедшие через отдаленные от оси части системы, не собираются в одну точку;

4) хроматическая аберрация ¾аберрация,связанная с зависимостьюпоказателя преломления материала линзы от длины волны света.

В данной работе изучаются сферическая и хроматическая аберрации.

1.4.1. Сферическая аберрация

Если на линзу направить пучок света, параллельный главной оптической оси, то лучи, прошедшие через различные участки линзы соберутся в разных точках на оси (рис. 6). Поэтому на экране, установленном перпендикулярно оси, даже в случае идеального точечного источника будут наблюдаться изображения в виде диска с неоднородным распределением освещенности. Если перед линзой поместить маску, имеющую форму узкого кольца, то сферическая аберрация практически исчезнет, но существенно уменьшится и интенсивность прошед-шего света. В качестве меры для сферической аберрации берут разность фокусных расстояний линзы для ее центральной части (маска в этом случае имеет вид небольшого отверстия) и для зоны, расположенной на краю линзы.

Сферическая аберрация сильнее проявляется для линз с малым фокусным расстоянием, причем она, в отличии от всех других аберраций, сохраняется в монохроматическом свете даже при расположении идеального точечного источника строго на главной оптической оси системы.

1.4.2. Х р о м а т и ч е с к а я а б е р р а ц и я

В прозрачных средах показатель преломления n растет с уменьшением длины волны света l. В видимой области спектра существует эмпирическая формула, описывающая зависимость показателя преломления n от длины волны света l:

где A, B, C, ... — константы, характерные для данного вещества.

Так как в формулу для фокусного расстояния линзы входит показатель преломления, то F является функцией от l. Поэтому изображение точечного немонохроматического источника уже не является точечным, а представляет собой совокупность пространственно разделенных точек разных цветов. Для протяженного источника это приводит к тому, что края изображения окрашиваются. В качестве меры хроматической аберрации принято брать разность фокусных расстояний линзы для крайних цветов видимого диапазона (красного и фиолетового).

Рис. 6. Сферическая аберрация в линзе

II. ЭКСПЕРИМЕНТ