|
|
ОПРЕДЕЛЕНИЕ ДЛИНЫ ВОЛНЫ СВЕТАС ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА Цель работы:пронаблюдать на опыте интерференцию света в тонкой пленке (в воздушном слое между линзой и пластинкой) в виде колец Ньютона и определить длину волны света с помощью колец Ньютона. Приборы и принадлежности: плосковыпуклая линза, поставленная выпуклой стороной на плоскопараллельную пластину и закрепленная на ней; микроскоп; источник света; линейка с миллиметровой шкалой. П р и м е ч а н и е: теория метода и описание установки приводятся в работе № 2.
1. Определение цены деления окулярной шкалы П р и м е ч а н и е: задание выполняется так же, как и в работе № 2. 2. Определение длины волны света Диаметр кольца Ньютона можно непосредственно измерить в делениях окулярной шкалы. Умножая этот результат на величину b, выраженную в мм/дел., получим диаметр в мм. Радиусы i-го и n-го темных колец в соответствии с формулой (2.5)
rт,i =
Возводя эти выражения в квадрат, и вычитая одно из другого, получим
Формула (3.2) справедлива и для светлых колец. Так как центр кольца устанавливается с большой погрешностью, в опыте измеряют не радиус, а диаметр кольца D. Тогда формула (3.2) принимает вид
откуда получаем формулу для вычисления длины волны света
Радиус линзы приведен в табл. 3.1, номер линзы указан на держателе линзы. В целях упрощения расчетов величину l =
Таблица 3.1
Выполнение работы
2.1. См. п. 2.1 в работе №2. 2.2. См. п.2.2 в работе №2. 2.3 См. п. 2.3 в работе №2. 2.4. По формуле (3.5) определить <l>. 2.5. Подсчитать абсолютную погрешность по формуле
где DT найти по формуле, аналогичной формуле (2.7). 2.6. Результаты измерений и вычислений занести в табл. 3.2. Записать окончательный результат в виде доверительного интервала с указанием надежности и относительной погрешности. Таблица 3.2
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Явление интерференции света. 2. Когерентность. 3. Оптическая длина пути и оптическая разность хода. 4. Условия максимумов и минимумов при интерференции. 5. Явления, происходящие при отражении: а) от среды, оптически более плотной; б) от среды, оптически менее плотной. 6. Линии равной толщины. Кольца Ньютона. 7. Вывод расчетной формулы. 8. Ход эксперимента по определению радиуса кривизны линзы или длины волны света с помощью колец Ньютона. 9. Вычисление погрешностей измерений.
ЛАБОРАТОРНАЯ РАБОТА № 4 ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ ДИФРАКЦИОННОЙ РЕШЕТКИ Цель работы: определить характеристики дифракционной решетки; измерить длину световой волны с помощью дифракционной решетки. Приборы и принадлежности: экспериментальная установка, дифракционная решетка.
Сведения из теории
Дифракцией света называют явления, вызванные нарушением цельности волновой поверхности. Дифракция проявляется в нарушении прямолинейности распространения колебаний. Волна огибает края препятствия и проникает в область геометрической тени. Дифракционные явления присущи всем волновым процессам, но проявляются особенно отчетливо лишь в тех случаях, когда длины волн излучений сопоставимы с размером препятствий. С точки зрения представлений геометрической оптики о прямолинейном распространении света граница тени за непрозрачным препятствием резко очерчена лучами, которые проходят мимо препятствия, касаясь его поверхности. Следовательно, явление дифракции необъяснимо с позиций геометрической оптики. По волновой теории Гюйгенса, рассматривающей каждую точку поля волны как источник вторичных волн, распространяющихся по всем направлениям, в том числе и в область геометрической тени препятствия, вообще необъяснимо возникновение сколько-нибудь отчетливой тени. Тем не менее, опыт убеждает нас в существовании тени, но не резко очерченной, как утверждает теория прямолинейного распространения света, а с размытыми краями.
Принцип Гюйгенса - Френеля
Особенность дифракционных эффектов состоит в том, что дифракционная картина в каждой точке пространства является результатом интерференции лучей от большого числа вторичных источников Гюйгенса. Объяснение этих эффектов было осуществлено Френелем и получило название принципа Гюйгенса - Френеля. Сущность принципа Гюйгенса - Френеля можно представить в виде нескольких положений: 1. Всю волновую поверхность, возбуждаемую каким-либо источником S0площадью S, можно разбить на малые участки с равными площадями dS, которые являются системой вторичных источников, испускающих вторичные волны. 2. Эти вторичные источники, эквивалентные одному и тому же первичному источнику S0, когерентны. Поэтому волны, распространяющиеся от источника S0, в любой точке пространства должны являться результатом интерференции всех вторичных волн. 3. Мощности излучения всех вторичных источников - участков волновой поверхности с одинаковыми площадями - одинаковы. 4. Каждый вторичный источник с площадью dS излучает преиму-щественно в направлении внешней нормали nк волновой поверхности в этой точке; амплитуда вторичных волн в направлении, составляющем с n угол a, тем меньше, чем больше угол a, и равна нулю при a ³ p / 2. 5. Амплитуда вторичных волн, дошедших до данной точки пространства, зависит от расстояния вторичного источника до этой точки: чем больше расстояние, тем меньше амплитуда. Принцип Гюйгенса - Френеля позволяет объяснить явление дифракции и дать методы ее количественного расчета.
Метод зон Френеля
Принцип Гюйгенса - Френеля объясняет прямолинейность распространения света в свободной от препятствий однородной среде. Чтобы показать это, рассмотрим действие сферической световой волны от точечного источника S0 в произвольной точке пространства P(рис. 4.1). Волновая поверхность такой волны симметрична относительно прямой S0P. Амплитуда искомой волны в точке P зависит от результата интерференции вторичных волн, излучаемых всеми участками dS поверхности S. Амплитуды и начальные фазы вторичных волн зависят от расположения соответствующих источников dS по отношению к точке P.
Френель предложил метод разбиения волновой поверхности на зоны (метод зон Френеля). По этому методу волновая поверхность разбивается на кольцевые зоны (рис. 4.1), построенные так, что расстояния от краев каждой зоны до точки Pотличаются на l/2(l - длина световой волны). Если обозначить через b расстояние от вершины волновой поверхности 0 до точки P, то расстояния b + k(l/2) образуют границы всех зон, где k - номер зоны. Колебания, приходящие в точку P от аналогичных точек двух соседних зон, противоположны по фазе, так как разность хода от этих зон до точки P равна l/2. Поэтому при наложении эти колебания взаимно ослабляют друг друга, и результирующая амплитуда выразится суммой:
A = A1- A2 + A3 - A4 + ... . (4.1)
Величина амплитуды Akзависит от площади DSkk-й зоны и угла akмежду внешней нормалью к поверхности зоны в любой ее точке и прямой, направленной из этой точки в точку P. Можно показать, что площадь DSkk-й зоны не зависит от номера зоны в условиях l<< b. Таким образом, в рассматриваемом приближении площади всех зон Френеля равновелики и мощность излучения всех зон Френеля - вторичных источников - одинакова. Вместе с тем, с увеличением k возрастает угол akмежду нормалью к поверхности и направлением на точку P, что приводит к уменьшению интенсивности излучения k-й зоны в данном направлении, т.е. к уменьшению амплитуды Ak по сравнению с амплитудами предыдущих зон. Амплитуда Ak уменьшается также вследствие увеличения расстояния от зоны до точки P с ростом k. В итоге A1 > A2 > A3 > A4 > ... > Ak > ...
Вследствие большого числа зон убывание Ak носит монотонный характер и приближенно можно считать, что
Переписав результирующую амплитуду (4.1) в виде
обнаруживаем, что, согласно (4.2) и с учетом малости амплитуды удаленных зон, все выражения в скобках равны нулю и уравнение (4.1) приводится к виду A = A1 / 2.(4.4)
Полученный результат означает, что колебания, вызываемые в точке P сферической волновой поверхностью, имеют амплитуду, даваемую половиной центральной зоны Френеля. Следовательно, свет от источника S0 в точку P распространяется в пределах очень узкого прямого канала, т.е. прямолинейно. В результате явления интерференции уничтожается действие всех зон, кроме первой.
Дифракция Френеля от простейших преград
Действие световой волны в некоторой точке P сводится к действию половины центральной зоны Френеля в том случае, если волна безгранична, так как только тогда действия остальных зон взаимно компенсируются и можно пренебречь действием удаленных зон. При конечном участке волны условия дифракции существенно отличаются от описанных выше. Однако и здесь применение метода Френеля позволяет предвидеть и объяснить особенности распространения световых волн. Рассмотрим несколько примеров дифракции Френеля от простых преград.
Дифракция на круглом отверстии. Пусть волна от источника S0 встречает на пути непрозрачный экран с круглым отверстием BC (рис. 4.2). Результат дифракции наблюдается на экране Э, параллельном плоскости отверстия. Легко определить дифракционный эффект в точке P экрана, расположенной против центра отверстия. Для этого достаточно построить на открытой части фронта волны BC зоны Френеля, соответствующие точке P. Если в отверстии BCукладывается k зон Френеля, то амплитуда Aрезультирующих колебаний в точке P зависит от четности и нечетности числа k, а так же от того, насколько велико абсолютное значение этого числа. Действительно, из формулы (4.1) вытекает, что в точке Pамплитуда суммарного колебания
(первое уравнение системы при нечетном k, второе - при четном) или, учитывая формулу (4.2) и тот факт, что амплитуды двух соседних зон мало отличаются по величине и можно считать Ak-1 приблизительно равным Ak ,имеем
где плюс соответствует нечетному числу зон k, укладывающихся на отверстии, а минус – четному. При небольшом числе зон k амплитуда Ak мало отличается от A1. Тогда результат дифракции в точке P зависит от четности k: при нечетном kнаблюдается максимум дифракции, при четном – минимум. Минимумы и максимумы будут тем больше отличаться друг от друга, чем ближе Akк A1 т.е. чем меньше k. Если отверстие открывает только центральную зону Френеля, амплитуда в точке P будет равна A1, она в два раза больше той, которая имеет место при полностью открытом волновом фронте (4.4), а интенсивность в этом случае в четыре раза больше, чем при отсутствии преграды. Напротив, при неограниченном увеличении числа зон k, амплитуда Akстремится к нулю (Ak<< A1) и выражение (4.5) превращается в (4.4). Свет в этом случае фактически распространяется так же, как и при отсутствии экрана с отверстием, т.е. прямолинейно. Отсюда вытекает вывод о том, что следствия из волновых представлений и представлений о прямолинейном распространении света начинают совпадать тогда, когда число открытых зон велико. Колебания от четных и нечетных зон Френеля взаимно ослабляют друг друга. Это приводит иногда к увеличению интенсивности света при закрывании непрозрачным экраном части волнового фронта, как это было в случае преграды с круглым отверстием, на котором укладывается только одна зона Френеля. Интенсивность света можно увеличить во много раз, если изготовить сложный экран - так называемую зонную пластинку (стеклянная пластинка с непрозрачным покрытием), которая закрывает все четные (или нечетные) зоны Френеля. Зонная пластинка действует подобно собирательной линзе. Действительно, если зонная пластинка закрывает все четные зоны, а число зон k = 2m, то из (4.1) следует
A = A1 + A3 +...+ A2m-1
или при небольшом числе зон, когда A2m-1 приблизительно равно A, A = mA1 , т.е. интенсивность света в точке P в (2m)2 раз больше, чем при беспрепятственном распространении света от источника в точку P, при этом A = A1 / 2, а интенсивность соответственно Дифракция на круглом диске. При размещении между источником S0и экраном круглого непрозрачного диска СВ закрывается одна или несколько первых зон Френеля (рис. 4.3). Если диск закроет k зон Френеля, то в точке P амплитуда суммарной волны
и, так как выражения в скобках можно принять равными нулю, аналогично (4.3) получаем A = Ak+1 / 2. (4.6)
Таким образом, в случае круглого непрозрачного диска в центре картины (точка P) при любом (как четном, так и нечетном) k получается светлое пятно. Если диск закрывает лишь часть первой зоны Френеля, тень на экране отсутствует, освещенность во всех точках такая же, как и при отсутствии преграды. С ростом радиуса диска первая открытая зона отдаляется от точки P и увеличивается угол aмежду нормалью к поверхности этой зоны в какой-либо точке и направлением излучения в сторону точки P (см. принцип Гюйгенса - Френеля). Поэтому интенсивность центрального максимума ослабевает при увеличении размеров диска ( Ak+1 << A1). Если диск закрывает много зон Френеля, интенсивность света в области геометрической тени практически всюду равна нулю и лишь вблизи границ наблюдения имеет место слабая интерференционная картина. В этом случае можно пренебречь явлением дифракции и пользоваться законом прямолинейного распространения света.
Дифракция Фраунгофера (дифракция в параллельных лучах)
В случае сферических волн результат дифракции зависит от трех параметров: длины волны излучения, испускаемого источником S0, геометрии препятствия (размеров щели, отверстия и т.д.) и расстояния от препятствия до экранов наблюдения. В условиях дифракции Фраунгофера осуществляется переход к плоским волнам, что исключает зависимость результата дифракции от третьей величины (расстояния от препятствия до экрана наблюдения), а геометрические размеры препятствия могут быть заранее учтены. В случае отверстия неизменных формы и размеров результат дифракции зависит только от изменения спектрального состава излучения, даваемого источником S0. Поэтому дифракционные явления в параллельных лучах могут использоваться для спектрального анализа состава излучения исследуемых веществ. Принципиальная схема наблюдения плоских волн (дифракция Фраунгофера) изображена на рис. 4.4. Свет от точечного источника S0 превращается линзой L1 в пучок параллельных лучей (плоскую волну), который проходит затем через отверстие в непрозрачном экране (круг, щель, и т.д.). Линза L2 собирает в различных точках своей фокальной плоскости, где расположен экран наблюдения Э, все лучи, прошедшие через отверстие, в том числе и лучи, отклонившиеся от первоначального направления в результате дифракции.
Лучи, дифрагирующие под одним углом, линза L2 собирает в одной точке фокальной плоскости Э. Так как наблюдение дифракции по методу Фраунгофера ведется в том месте, где свет собирается линзой L2, то явление значительно выигрывает в яркости и наблюдение дифракционной картины облегчается. Рассмотрим несколько случаев дифракции Фраунгофера.
Дифракция от одной щели. Практически щель представляется прямоугольным отверстием, длина которого значительно больше ширины. В этом случае изображение точки S0 (рис. 4.4) растянется в полоску с минимумами и максимумами по направлению, перпендикулярному к щели, ибо свет дифрагирует вправо и влево от щели (рис. 4.5). Если наблюдать изображение источника в направлении, перпендикулярном направлению образующей щели, то можно ограничиться рассмотрением дифракционной картины в одном измерении (вдоль х). Так как плоскость щели совпадает с фронтом падающей волны, то в соответствии с принципом Гюйгенса - Френеля точки щели являются вторичными источниками волн, колеблющихся в одной фазе. Разобьем площадь щели на ряд узких полосок равной ширины, параллельных образующей щели. Фазы волн от разных полосок на одинаковых расстояниях равны, амплитуды также равны, ибо выбранные элементы имеют равные площади и одинаково наклонены к направлению наблюдения. Если бы при прохождении света через щель соблюдался закон прямолинейного распространения света (не было бы дифракции), то на экране Э, установленном в фокальной плоскости линзы L2, получалось бы изображение щели. Следовательно, направление j = 0 определяет недифрагированную волну с амплитудой A0 , равной амплитуде волны, посылаемой всей щелью. Из-за дифракции световые лучи отклоняются от прямолинейного направления на угол j. Отклонение вправо и влево симметрично относительно осевой линии OC0 (рис. 4.5). Для отыскания действия всей щели в направлении, определяемом углом j, необходимо учесть разность фаз, характеризующую волны, доходящие до точки наблюдения Cj от различных полосок (зон Френеля). Проведем плоскость FD, перпендикулярную к направлению дифрагированных лучей и представляющую фронт новой волны. Так как линза не вносит дополнительной разности хода лучей, ход всех лучей от плоскости FD до точки Cj одинаков. Следовательно, полная разность хода лучей от щели FEзадается отрезком ED. Проведем плоскости, параллельные волновой поверхности FD, таким образом, чтобы они разделили отрезок EDна несколько участков, каждый из которых имеет длинуl/2 (рис. 4.5). Эти плоскости разделят щель на вышеупомянутые полоски - зоны Френеля, причем разность хода от соседних зон равна l/2 в соответствии с методом Френеля. Тогда результат дифракции в точке Cj определится числом зон Френеля, укладывающихся в щели (см. дифракцию Френеля на круглом отверстии): если число зон четное (z = 2k), в точке Cjнаблюдается минимум дифракции, если z - нечетное (z = 2k+1), в точке Cj- максимум дифракции. Число зон Френеля, укладывающихся на щели FE, определяется тем, сколько раз в отрезке ED содержится l/2 т.е. В итоге для положения максимумов дифракции получаем условие
а sin j = ±(2k + 1)l / 2,(4.7)
дляминимумов дифракции
а sin j = ± 2kl /2,(4.8)
где k = 1,2,3.. - целые числа. Величина k, принимающая значения чисел натурального ряда, называется порядком дифракционного максимума. Знаки ± в формулах (4.7) и (4.8) соответствуют лучам света, дифрагирующим от щели под углами +j и -j и собирающимся в побочных фокусах линзы L2: Cj и C-j, симметричных относительно главного фокуса C0. В направлении j = 0 наблюдается самый интенсивный центральный максимум нулевого порядка. Положение максимумов дифракции по формуле (4.7) соответствует углам
На рис. 4.6 приведена кривая распределения интенсивности света в функции sin j. Положение центрального максимума (j = 0) не зависит от длины волны и, следовательно, является общим для всех длин волн. Поэтому в случае белого света центр дифракционной картины представится в виде белой полоски. Из рис. 4.6 и формул (4.7) и (4.8) ясно, что положение максимумов и минимумов зависит от длины волны. Поэтому простое чередование темных и светлых полос имеет место только при монохроматическом свете. В случае белого света дифракционные картины для волн с разными lсдвигаются в соответствии с длиной волны. Центральный максимум белого цвета имеет радужную окраску только по краям (на ширине щели укладывается одна зона Френеля). Боковые максимумы для разных длин волн уже не совпадают между собой; ближе к центру располагаются максимумы, соответствующие более коротким волнам. Длинноволновые максимумы отстоят друг от друга дальше (j = arcsin l/2), чем коротковолновые. Поэтому дифракционный максимум представляет собой спектр, обращенный к центру фиолетовой частью.
Дифракционная решетка
Дифракционная решетка представляет собой систему большого числа одинаковых по ширине и параллельных друг другу щелей, лежащих в одной плоскости и разделенных непрозрачными промежутками, равными по ширине. Дифракционная решетка изготавливается путем нанесения параллельных штрихов на поверхность стекла. Число штрихов на 1 мм определяется областью спектра исследуемого излучения и изменяется от 300 мм-1 в инфракрасной области до 1200 мм-1 в ультрафиолетовой.
Пусть решетка состоит из N параллельных щелей с шириной каждой щели aи расстоянием между соседними щелями b (рис. 4.7). Сумма a + b = dназывается периодом или постоянной дифракционной решетки. Пусть на решетку нормально падает плоская монохроматическая волна. Требуется исследовать интенсивность света, распространяющегося в направлении, составляющем угол j с нормалью к плоскости решетки. Кроме распределения интенсивности из-за дифракции на каждой щели, имеет место перераспределение световой энергии за счет интерференции волн от N щелей когерентных источников. При этом минимумы будут находиться на прежних местах, ибо условие минимума дифракции для всех щелей (рис. 4.8) одинаково. Эти минимумы называются главными. Условие главных минимумов a sin j = ± klсовпадает с условием (4.8). Положение главных минимумов sin j = ± l/a, 2l /a,... показано на рис. 4.8.
Однако в случае многих щелей к главным минимумам, создаваемым каждой щелью в отдельности, добавляются минимумы, возникающие в результате интерференции света, прошедшего через различные щели. На рис. 4.8 для примера показано распределение интенсивности и расположение максимумов и минимумов в случае двух щелей с периодом dи шириной щели a. В одном и том же направлении все щели излучают энергию колебаний одинаковой амплитуды. И результат интерференции зависит от разности фаз колебаний, исходящих от сходственных точек соседних щелей (например, Cи E, B и F), или от оптической разности хода ED от сходственных точек двух соседних щелей до точки Cj. Для всех сходственных точек эта разность хода одинакова. Если ED = ± klили, так как ED = d sin j, d sin j = ± kl , k = 0,1,2..., (4.9)
колебания соседних щелей взаимно усиливают друг друга, и в точке Cj фокальной плоскости линзы наблюдается максимум дифракции. Амплитуда суммарного колебания в этих точках экрана максимальна:
Amax = N Aj ,(4.10)
где Aj - амплитуда колебания, посылаемого одной щелью под углом j. Интенсивность света Jmax = N2Aj2 = N2Jj.(4.11) Поэтому формула (4.9) определяет положение главных максимумов интенсивности. Число kдает порядок главного максимума. Положение главных максимумов (4.9) определяется соотношением
Максимум нулевого порядка один и расположен в точке C0, максимумов первого, второго и т.д. порядков по два и расположены они симметрично относительно C0, на что указывает знак +. На рис. 4.8 показано положение главных максимумов. Кроме главных максимумов, имеется большое число более слабых побочных максимумов, разделенных добавочными минимумами. Побочные максимумы значительно слабее главных. Расчет показывает, что интенсивность побочных максимумов не превышает 1/23 интенсивности ближайшего главного максимума. В главных максимумах амплитуда в Nраз, а интенсивность в N2раз больше амплитуды, даваемой в соответствующем месте одной щелью. Четко локализованные в пространстве линии с увеличенной яркостью легко обнаруживаются и могут быть использованы в целях спектроскопических исследований. По мере удаления от центра экрана интенсивность дифракционных максимумов убывает (увеличивается расстояние от источников). Поэтому не удается наблюдать все возможные дифракционные максимумы. Заметим, что количество дифракционных максимумов, даваемых решеткой по одну сторону экрана, определяется условием ½sinj½ £ 1 (j = p / 2 - максимальный угол дифракции), откуда с учетом (4.9)
При этом не следует забывать, что k- целое число. Положение главных максимумов зависит от длины волны l. Поэтому при освещении дифракционной решетки белым светом все максимумы, кроме центрального (k= 0), разложатся в спектр, обращенный фиолетовым концом к центру дифракционной картины. Таким образом, дифракционная решетка может служить для исследования спектрального состава света, т.е. для определения частот (или длин волн) и интенсивности всех его монохроматических компонент. Применяемые для этого приборы называются дифракционными спектрографами, если исследуемый спектр регистрируется с помощью фотопластинки, и дифракционными спектроскопами, если спектр наблюдается визуально.
|
|
 ,rт,n =
,rт,n =  . (3.2)
. (3.2) , (3.3)
, (3.3) . (3.4)
. (3.4) обозначим через T. Тогда
обозначим через T. Тогда . (3.5)
. (3.5) ,
,
 . (4.2)
. (4.2) , (4.3)
, (4.3)
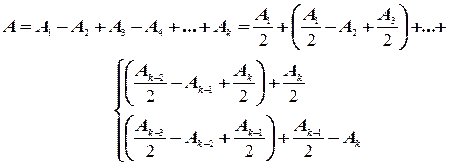
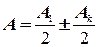 , (4.5)
, (4.5)
 / 4 .
/ 4 .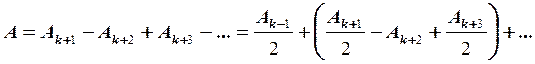


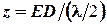 . Отрезок ED, выраженный через ширину щели а и угол дифракции j, запишется как ED = а sin j.
. Отрезок ED, выраженный через ширину щели а и угол дифракции j, запишется как ED = а sin j. ,
, 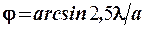 ,
,  и т.д.
и т.д.


 . (4.12)
. (4.12) . (4.13)
. (4.13)