Ограниченность последовательности, связь с пределом Если множество значений 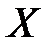 членов последовательности членов последовательности  является ограниченным сверху (снизу), то является ограниченным сверху (снизу), то  называется ограниченной сверху (снизу) последовательностью. называется ограниченной сверху (снизу) последовательностью.
Если  ограничена и сверху и снизу, то она называется ограниченной последовательностью ограничена и сверху и снизу, то она называется ограниченной последовательностью
Это формальное определение ограниченной последовательности можно записать в другом виде:
, при этом можно брать s New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="22"/></w:rPr></m:ctrlPr></m:dPr><m:e><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>b</m:t></m:r></m:e></m:d></m:e></m:d></m:e></m:func></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 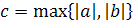 . .
Точные грани ограниченной последовательности – это точные грани множества её значений: 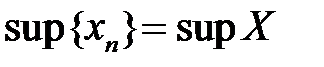 , , 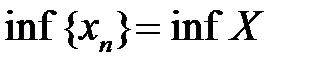 . .
Если  не является ограниченной, то она называется неограниченной последовательностью, то есть неограниченная последовательность не является ограниченной либо сверху, либо снизу, либо и сверху и снизу. не является ограниченной, то она называется неограниченной последовательностью, то есть неограниченная последовательность не является ограниченной либо сверху, либо снизу, либо и сверху и снизу.
Например,
1) 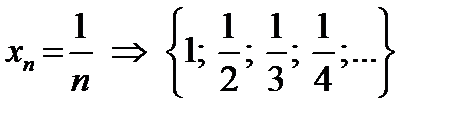 – это ограниченная последовательность, так как – это ограниченная последовательность, так как 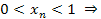 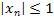 при при 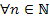 ; ;
2) 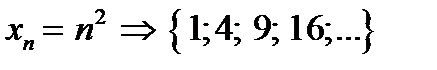 – это неограниченная последовательность, так как не является ограниченной сверху. – это неограниченная последовательность, так как не является ограниченной сверху.
Свойство ограниченности/неограниченности последовательности связывается с ее пределом двумя теоремами.
| Теорема об ограниченности сходящейся последовательности
| Если последовательность 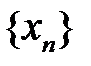 имеет конечный предел, то она является ограниченной. имеет конечный предел, то она является ограниченной.
|
wПусть 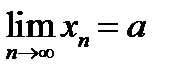 . По определению конечного предела в любой . По определению конечного предела в любой  - окрестности точки - окрестности точки 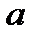
находятся все члены последовательности, начиная с некоторого номера. Поэтому, если
взять 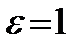 , то вне промежутка , то вне промежутка  может находиться только конечное количество может находиться только конечное количество
чисел  (рис. 19): (рис. 19):
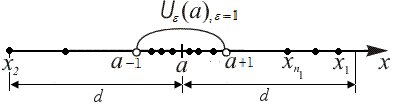
Рис.19
Обозначим через 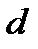 наибольшее расстояние от числа наибольшее расстояние от числа  до чисел до чисел 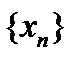 : :
 . .
Тогда для 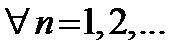 будет верно, что будет верно, что  . Это по определению и означает ограниченность последовательности . Это по определению и означает ограниченность последовательности 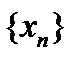 .v .v
Обратное утверждение не является верным, то есть из ограниченности последовательности не следует существование её конечного предела.
Например, числа 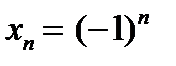 образуют ограниченную, но не сходящуюся последовательность. образуют ограниченную, но не сходящуюся последовательность.
| Теорема о неограниченности бесконечно большой последовательности
| | Любая бесконечно большая последовательность является неограниченной.
| w Пусть  (или (или  или или 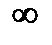 ). По определению бесконечного предела в любой ). По определению бесконечного предела в любой  находятся все члены этой последовательности, начиная с некоторого номера, то есть верно неравенство находятся все члены этой последовательности, начиная с некоторого номера, то есть верно неравенство  при при 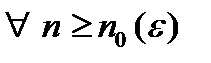 . Отсюда следует, что . Отсюда следует, что 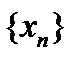 не может быть ограниченной сверху, так как в противном случае существовало бы число не может быть ограниченной сверху, так как в противном случае существовало бы число  , такое что , такое что 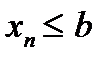 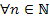 ; но это бы противоречило неравенству ; но это бы противоречило неравенству  , если число , если число 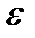 взять таким, что взять таким, что 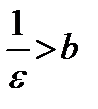 , (рис. 20). , (рис. 20).
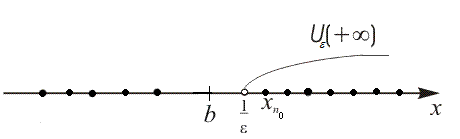
Рис. 20
Таким образом, 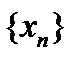 является неограниченной, так как она не ограничена сверху. v является неограниченной, так как она не ограничена сверху. v
Обратное утверждение не является верным, то есть не всякая неограниченная последовательность является бесконечно большой.
Например,  – это неограниченная последовательность, но не бесконечно большая. – это неограниченная последовательность, но не бесконечно большая.
В результате доказанных теорем можно схематично изобразить связь понятий ограниченности и предела последовательности:
Словами эта связь формулируется следующим образом:
ограниченность является необходимым условием для сходимости последовательности, но недостаточным; неограниченность является необходимым условием для бесконечно большой последовательности, но недостаточным.
2.8. Упражнения для самостоятельной работы
1.Пользуясь признаком существования конечного предела, докажите, что
1) 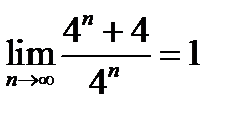 ; 2) ; 2) 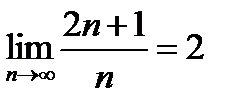 ; ;
3)  ; 4) ; 4)  . .
2.Среди последовательностей с общим членом  укажите номера сходящихся, бесконечно больших, бесконечно малых последовательностей и последовательностей, не имеющих предела: укажите номера сходящихся, бесконечно больших, бесконечно малых последовательностей и последовательностей, не имеющих предела:
1) 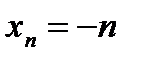 ; 2) ; 2) 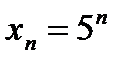 ; 3) ; 3) 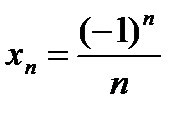 ; 4) ; 4) 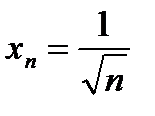 ; ;
5) 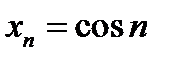 ; 6) ; 6) 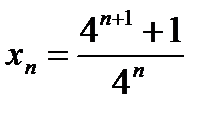 ; 7) ; 7) 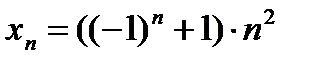 ; 8) ; 8) 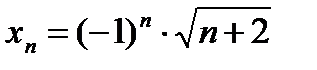 . .
3.Среди последовательностей с общим членом  укажите номера ограниченных и неограниченных последовательностей; для каждой ограниченной последовательности укажите её точные грани: укажите номера ограниченных и неограниченных последовательностей; для каждой ограниченной последовательности укажите её точные грани:
1) 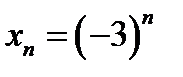 ; 2) ; 2)  ; 3) ; 3) 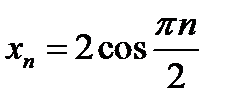 ; ;
4)  ; 5) ; 5) 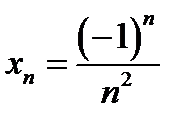 ; 6) ; 6)  ; ;
7)  8) 8) 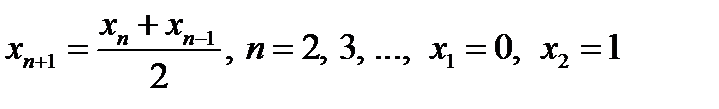 . .
Ответы к упражнениям для самостоятельной работы
2. Сходящиеся последовательности: 3), 4), 6);
бесконечно большие последовательности: 1), 2), 8);
бесконечно малые последовательности: 3), 4);
последовательности, которые не имеют предела: 5), 7).
3.Ограниченные последовательности: 2), 3), 5), 6), 7), 8);
неограниченные последовательности: 1), 4);
точные грани ограниченных последовательностей:
2) 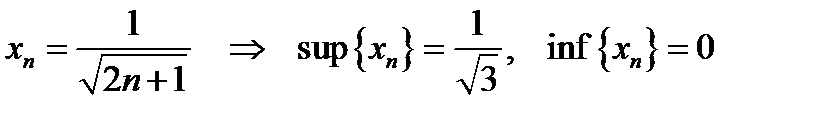 ; ;
3)  ; ;
5) 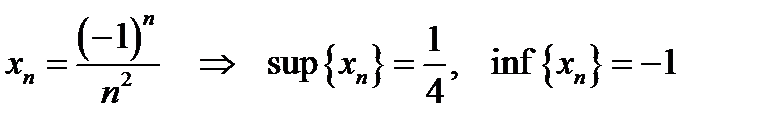 ; ;
6) 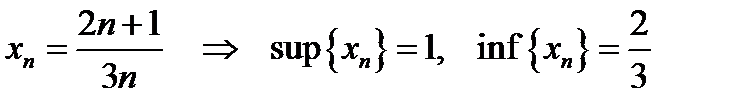 ; ;
7) 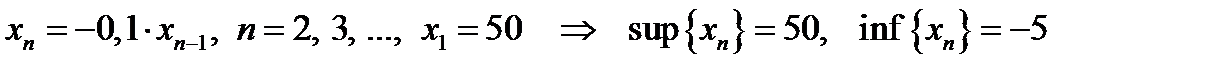 ; ;
8) 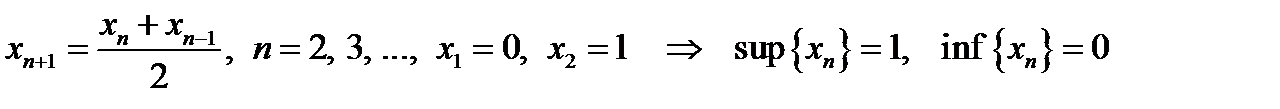 . .
|
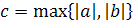 .
.
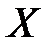 членов последовательности
членов последовательности  является ограниченным сверху (снизу), то
является ограниченным сверху (снизу), то 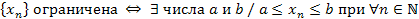
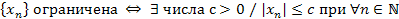
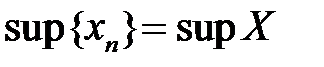 ,
, 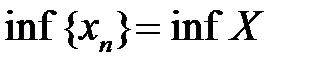 .
.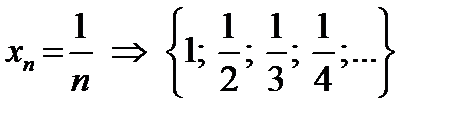 – это ограниченная последовательность, так как
– это ограниченная последовательность, так как 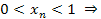
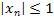 при
при 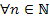 ;
;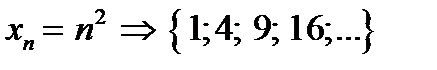 – это неограниченная последовательность, так как не является ограниченной сверху.
– это неограниченная последовательность, так как не является ограниченной сверху.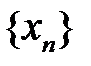 имеет конечный предел, то она является ограниченной.
имеет конечный предел, то она является ограниченной.
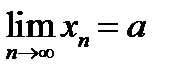 . По определению конечного предела в любой
. По определению конечного предела в любой  - окрестности точки
- окрестности точки 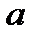
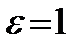 , то вне промежутка
, то вне промежутка  может находиться только конечное количество
может находиться только конечное количество (рис. 19):
(рис. 19):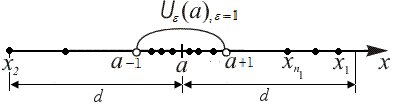
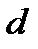 наибольшее расстояние от числа
наибольшее расстояние от числа  до чисел
до чисел 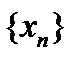 :
: .
.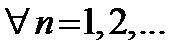 будет верно, что
будет верно, что  . Это по определению и означает ограниченность последовательности
. Это по определению и означает ограниченность последовательности 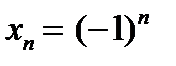 образуют ограниченную, но не сходящуюся последовательность.
образуют ограниченную, но не сходящуюся последовательность. (или
(или  или
или 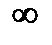 ). По определению бесконечного предела в любой
). По определению бесконечного предела в любой  находятся все члены этой последовательности, начиная с некоторого номера, то есть верно неравенство
находятся все члены этой последовательности, начиная с некоторого номера, то есть верно неравенство  при
при 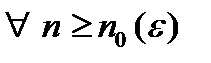 . Отсюда следует, что
. Отсюда следует, что  , такое что
, такое что 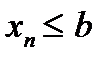
 , если число
, если число 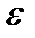 взять таким, что
взять таким, что 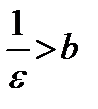 , (рис. 20).
, (рис. 20).
 – это неограниченная последовательность, но не бесконечно большая.
– это неограниченная последовательность, но не бесконечно большая.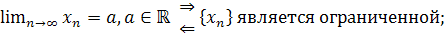
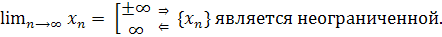
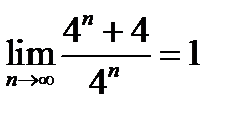 ; 2)
; 2) 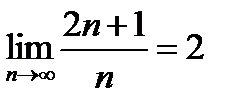 ;
; ; 4)
; 4)  .
. укажите номера сходящихся, бесконечно больших, бесконечно малых последовательностей и последовательностей, не имеющих предела:
укажите номера сходящихся, бесконечно больших, бесконечно малых последовательностей и последовательностей, не имеющих предела: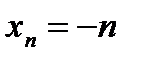 ; 2)
; 2) 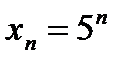 ; 3)
; 3) 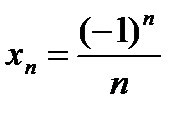 ; 4)
; 4) 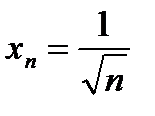 ;
;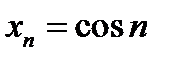 ; 6)
; 6) 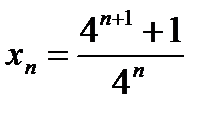 ; 7)
; 7) 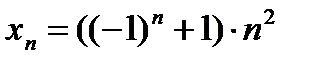 ; 8)
; 8) 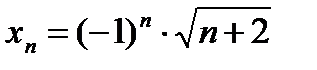 .
.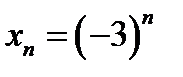 ; 2)
; 2)  ; 3)
; 3) 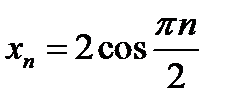 ;
; ; 5)
; 5) 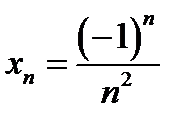 ; 6)
; 6)  ;
; 8)
8) 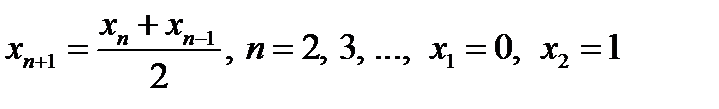 .
.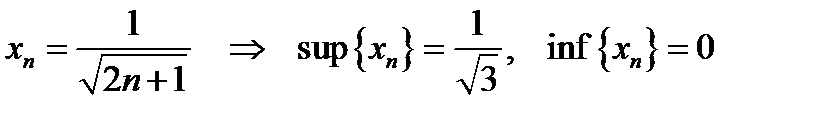 ;
; ;
;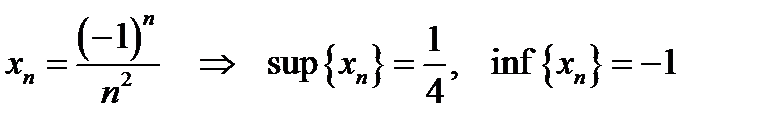 ;
;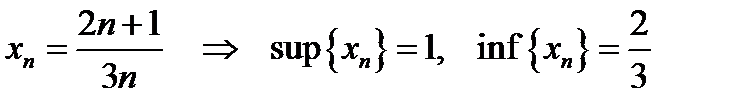 ;
;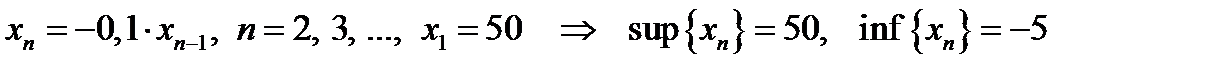 ;
;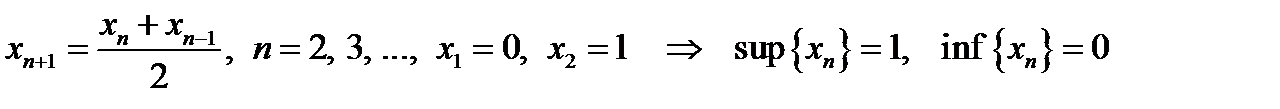 .
.