Примеры доказательства пределов функции Используя определение предела на языке «ε-δ», рассмотрим доказательства следующих пределов:
1)  ; 2) ; 2)  ; 3) ; 3) 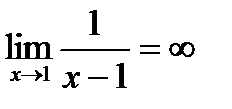 . .
Решение
1)Запишем определение конечного предела функции в конечной точке на языке «ε-δ»:
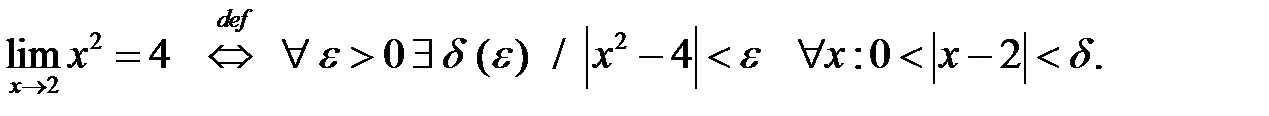
Зафиксируем произвольно малое число ε > 0 и найдём все значения x , для которых выполняется неравенство  : :


 . .
Далее нужно убедиться, что в полученном множестве значений x выделяется окрестность точки x=2; для этого можно провести арифметический тест, зафиксировав какое-нибудь малое значение ε>0 , или просто проанализировать получившиеся промежутки для х.Например, при ε=0,1получим, что
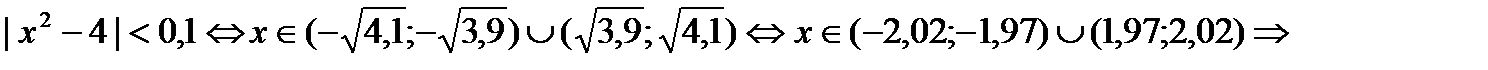
очевидно, что второй промежуток (1,97 ; 2,02)образует окрестность точки x=2 и, чтобы её зафиксировать как симметричную δ-окрестность, достаточно взять число δ, не превышающее величины меньшего из расстояний от точки x=2 до концов промежутка, то есть δ=min(  -2 ; 2- -2 ; 2-  ). ).
Таким образом, в рассматриваемом примере промежуток  образует окрестность точки x=2; симметрировать и измерить эту окрестность можно числом образует окрестность точки x=2; симметрировать и измерить эту окрестность можно числом
 ≤ min{δ1; δ2}, где ≤ min{δ1; δ2}, где 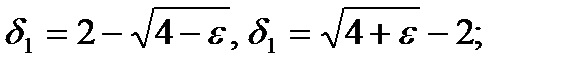
Формулируем итог проведенных рассуждений:
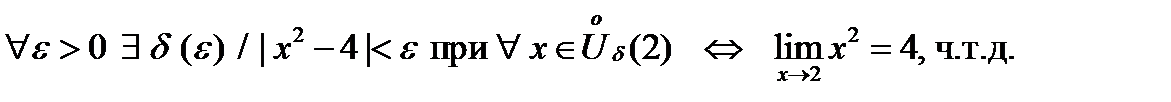
Заметим, что другой промежуток  , получившийся как часть решения неравенства , получившийся как часть решения неравенства  , образует окрестность точки x=–2и указывает на то, что , образует окрестность точки x=–2и указывает на то, что  , что легко подтверждается и графиком функции y=x2. , что легко подтверждается и графиком функции y=x2.
Обратите еще внимание, что факт  никак не зависит от значения функции f(x) в точке x=2, но характеризует только лишь поведение f(x)в малой окрестности этой точки. Например, если функцию y=x2 переопределить так, что никак не зависит от значения функции f(x) в точке x=2, но характеризует только лишь поведение f(x)в малой окрестности этой точки. Например, если функцию y=x2 переопределить так, что  , то останется верным предел , то останется верным предел  . .
2)  . .
 Зафиксируем произвольно малое число ε>0 и найдём все значения х , при которых выполняется неравенство Зафиксируем произвольно малое число ε>0 и найдём все значения х , при которых выполняется неравенство

Получившиеся промежутки образуют окрестность точки х=∞. Выделить из неё часть, симметричную относительно 0 и измеряемую числом δ, можно следующим образом:
  
Таким образом, доказано, что для ∀ ε>0, сколь малым бы его ни задавать, находится
число  , такое что неравенство , такое что неравенство  выполняется при выполняется при  . Это и означает по определению предела функции, что . Это и означает по определению предела функции, что  , ч.т.д. , ч.т.д.
 3) 3)
 Зафиксируем произвольно малое число ε>0 и найдём все значения х, при которых выполняется неравенство Зафиксируем произвольно малое число ε>0 и найдём все значения х, при которых выполняется неравенство

|   
Очевидно, что получившиеся промежутки образуют проколотую окрестность точки x=1, причём, окрестность сразу получилась симметричной относительно точки x=1 и её длина равна 2δ, где δ=ε.
 Таким образом, строго доказано требуемое значение предела: Таким образом, строго доказано требуемое значение предела:
|
 Замечание к примерам 2) и 3) Замечание к примерам 2) и 3)
На графике функции легко отслеживается её предельное поведение в точке х=1 и при x→∞ :
 означает, что значения функции означает, что значения функции  становятся сколь угодно близкими к нулю, если брать значения аргумента х достаточно большими по модулю; становятся сколь угодно близкими к нулю, если брать значения аргумента х достаточно большими по модулю;
 означает, что значения функции означает, что значения функции  становятся сколь угодно большими по модулю, если брать значения аргумента х достаточно близкими к числу х=1. становятся сколь угодно большими по модулю, если брать значения аргумента х достаточно близкими к числу х=1.
Заметьте, что в точке х=1 данная функция не определена, при х=∞ никакая функция не имеет значения, но с помощью пределов  и и  мы вполне представляем локальную динамику поведения функции в окрестностях этих точек. мы вполне представляем локальную динамику поведения функции в окрестностях этих точек.
6.8.Упражнения для самостоятельной работы
Задача 1
Используя строгое определение предела функции на языке «ε-δ», докажите, что 
   1) 2) 3) 4) 1) 2) 3) 4)
| | проиллюстрируйте каждый предел с помощью графика соответствующей функции.
| Задача 2
Используя определение предела на языке последовательностей (по Гейне), докажите, что  не существует. (Подсказка: для доказательства сформулируйте определение предела функции y=cos x при х→∞ на языке последовательностей и постройте хотя бы две последовательности {xn}, такие, что не существует. (Подсказка: для доказательства сформулируйте определение предела функции y=cos x при х→∞ на языке последовательностей и постройте хотя бы две последовательности {xn}, такие, что  , но соответствующие им последовательности значений функции имеют разные пределы.) , но соответствующие им последовательности значений функции имеют разные пределы.)
Основные свойства пределов функций. Односторонние пределы
7.1. Единственность предела. 71
7.2. Предел постоянной функции. 72
7.3. Переход к переделу в равенстве или неравенстве. 73
7.4. О пределе зажатой функции. 74
7.5. Признак существования конечного предела. 75
7.6. Сохранение функцией знака своего конечного предела. 76
7.7. Односторонние пределы функции и их связь с обычным пределом.. 78
7.8. Упражнения для самостоятельной работы.. 80
Единственность предела
| Теорема о единственности предела
| Если существует  то этот предел является единственным, т.е. функция то этот предел является единственным, т.е. функция  не может иметь двух различных пределов в одной точке не может иметь двух различных пределов в одной точке  . .
|
w Теорема доказывается методом от противного. Допустим, что в точке  функция функция  имеет два различных предела: имеет два различных предела:  и и  . Далее будем использовать определение предела функции на языке последовательностей (по Коши): . Далее будем использовать определение предела функции на языке последовательностей (по Коши):
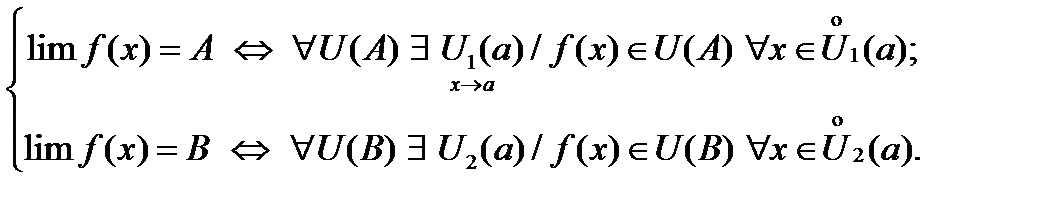
Теперь используем известные свойства окрестностей:
— окрестности двух различных точек  и и  всегда можно назначить так, чтобы они не пересекались; всегда можно назначить так, чтобы они не пересекались;
— окрестности одной и той же точки  всегда пересекаются, и их пересечение также является окрестностью точки всегда пересекаются, и их пересечение также является окрестностью точки  : :
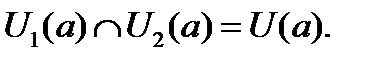
Тогда для  будем получать, что будем получать, что  и и  , что невозможно, так как: , что невозможно, так как:
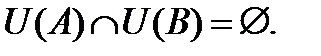
Получившееся противоречие указывает на то, что неверным является предположение о двух различных пределах функции  в одной точке в одной точке  . Следовательно, верным является противоположное утверждение: если предел . Следовательно, верным является противоположное утверждение: если предел  существует, то он является единственным. существует, то он является единственным.
Заметим, что приведённое доказательство теоремы остаётся справедливым для любых случаев  и и  .v .v
Предел постоянной функции
| Теорема о пределе постоянной функции
| Предел постоянной функции  , ,  равен этой постоянной в любой точке равен этой постоянной в любой точке  , которая является точкой сгущения множества , которая является точкой сгущения множества  : :

|
w Так как  где где  , то любая последовательность значений аргумента , то любая последовательность значений аргумента  , сходящаяся к точке , сходящаяся к точке  , будет давать стационарную последовательность значений функции , будет давать стационарную последовательность значений функции  , пределом которой является постоянная , пределом которой является постоянная  . Следовательно, на основании определения предела функции по Гейне, заключаем, что . Следовательно, на основании определения предела функции по Гейне, заключаем, что  . .
Заметим, что в доказательстве использовалось данное о том, что  есть точка сгущения ООФ есть точка сгущения ООФ  , так как только при этом условии можно рассматривать последовательность , так как только при этом условии можно рассматривать последовательность  .v .v
|
 , получившийся как часть решения неравенства
, получившийся как часть решения неравенства  , образует окрестность точки x=–2и указывает на то, что
, образует окрестность точки x=–2и указывает на то, что  , что легко подтверждается и графиком функции y=x2.
, что легко подтверждается и графиком функции y=x2.



 ; 2)
; 2)  ; 3)
; 3) 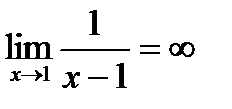 .
.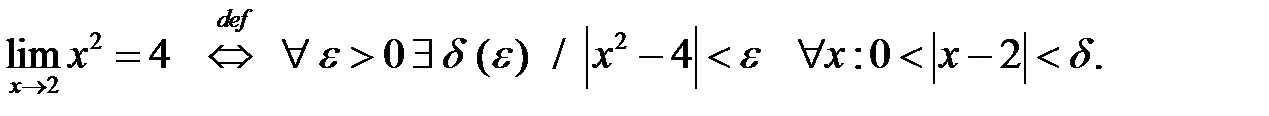
 :
:





 .
.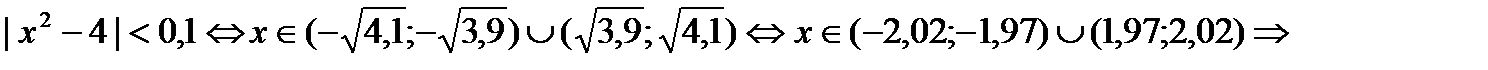
 -2 ; 2-
-2 ; 2-  ).
). образует окрестность точки x=2; симметрировать и измерить эту окрестность можно числом
образует окрестность точки x=2; симметрировать и измерить эту окрестность можно числом ≤ min{δ1; δ2}, где
≤ min{δ1; δ2}, где 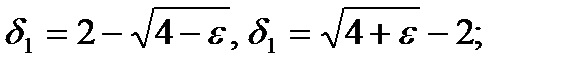






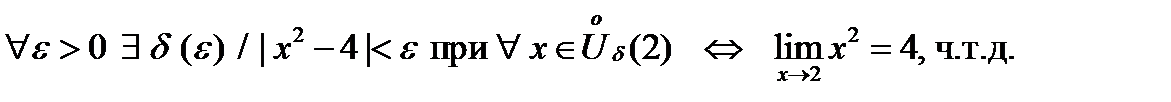
 никак не зависит от значения функции f(x) в точке x=2, но характеризует только лишь поведение f(x)в малой окрестности этой точки. Например, если функцию y=x2 переопределить так, что
никак не зависит от значения функции f(x) в точке x=2, но характеризует только лишь поведение f(x)в малой окрестности этой точки. Например, если функцию y=x2 переопределить так, что  , то останется верным предел
, то останется верным предел  .
. Зафиксируем произвольно малое число ε>0 и найдём все значения х , при которых выполняется неравенство
Зафиксируем произвольно малое число ε>0 и найдём все значения х , при которых выполняется неравенство

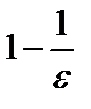

 , такое что неравенство
, такое что неравенство  выполняется при
выполняется при  . Это и означает по определению предела функции, что
. Это и означает по определению предела функции, что  , ч.т.д.
, ч.т.д. 3)
3) Зафиксируем произвольно малое число ε>0 и найдём все значения х, при которых выполняется неравенство
Зафиксируем произвольно малое число ε>0 и найдём все значения х, при которых выполняется неравенство



 Таким образом, строго доказано требуемое значение предела:
Таким образом, строго доказано требуемое значение предела: Замечание к примерам 2) и 3)
Замечание к примерам 2) и 3)

 становятся сколь угодно близкими к нулю, если брать значения аргумента х достаточно большими по модулю;
становятся сколь угодно близкими к нулю, если брать значения аргумента х достаточно большими по модулю;
 означает, что значения функции
означает, что значения функции  становятся сколь угодно большими по модулю, если брать значения аргумента х достаточно близкими к числу х=1.
становятся сколь угодно большими по модулю, если брать значения аргумента х достаточно близкими к числу х=1. и
и  мы вполне представляем локальную динамику поведения функции в окрестностях этих точек.
мы вполне представляем локальную динамику поведения функции в окрестностях этих точек.


 1) 2) 3) 4)
1) 2) 3) 4) не существует. (Подсказка: для доказательства сформулируйте определение предела функции y=cos x при х→∞ на языке последовательностей и постройте хотя бы две последовательности {xn}, такие, что
не существует. (Подсказка: для доказательства сформулируйте определение предела функции y=cos x при х→∞ на языке последовательностей и постройте хотя бы две последовательности {xn}, такие, что  , но соответствующие им последовательности значений функции имеют разные пределы.)
, но соответствующие им последовательности значений функции имеют разные пределы.) то этот предел является единственным, т.е. функция
то этот предел является единственным, т.е. функция  не может иметь двух различных пределов в одной точке
не может иметь двух различных пределов в одной точке  .
.
 функция
функция  имеет два различных предела:
имеет два различных предела:  и
и  . Далее будем использовать определение предела функции на языке последовательностей (по Коши):
. Далее будем использовать определение предела функции на языке последовательностей (по Коши):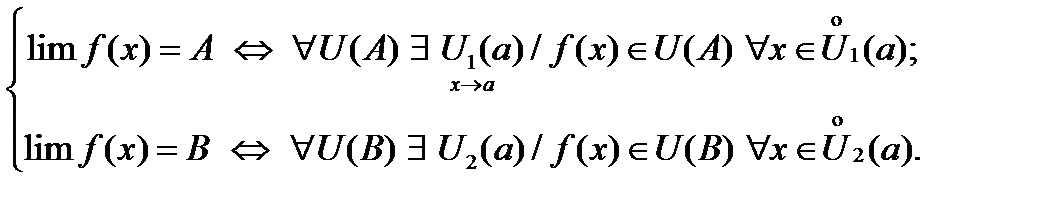
 и
и  всегда можно назначить так, чтобы они не пересекались;
всегда можно назначить так, чтобы они не пересекались; всегда пересекаются, и их пересечение также является окрестностью точки
всегда пересекаются, и их пересечение также является окрестностью точки  :
: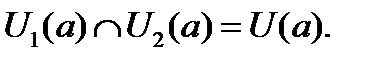
 будем получать, что
будем получать, что  и
и  , что невозможно, так как:
, что невозможно, так как: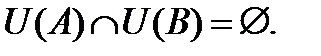
 в одной точке
в одной точке  . Следовательно, верным является противоположное утверждение: если предел
. Следовательно, верным является противоположное утверждение: если предел  существует, то он является единственным.
существует, то он является единственным. и
и  .v
.v ,
,  равен этой постоянной в любой точке
равен этой постоянной в любой точке  , которая является точкой сгущения множества
, которая является точкой сгущения множества  :
:

 где
где  , то любая последовательность значений аргумента
, то любая последовательность значений аргумента  , сходящаяся к точке
, сходящаяся к точке  , будет давать стационарную последовательность значений функции
, будет давать стационарную последовательность значений функции  , пределом которой является постоянная
, пределом которой является постоянная  . Следовательно, на основании определения предела функции по Гейне, заключаем, что
. Следовательно, на основании определения предела функции по Гейне, заключаем, что  .
. есть точка сгущения ООФ
есть точка сгущения ООФ  , так как только при этом условии можно рассматривать последовательность
, так как только при этом условии можно рассматривать последовательность  .v
.v