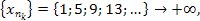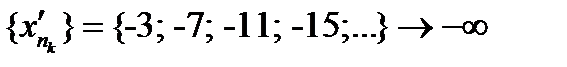Принцип компактности отрезка Ранее в параграфе 2 было показано, что если последовательность 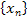 имеет конечный предел: имеет конечный предел:  , то она является ограниченной. При этом обратное неверно, то есть не всякая ограниченная последовательность имеет предел. Например, , то она является ограниченной. При этом обратное неверно, то есть не всякая ограниченная последовательность имеет предел. Например,  ограничена, но предела не имеет. ограничена, но предела не имеет.
Но, можно доказать, что если вся ограниченная последовательность может не иметь предела, то у нее всегда существует подпоследовательность, которая имеет конечный предел. Это утверждение называется принципом компактности отрезка, или теоремой Больцано – Вейерштрасса.
| Теорема Больцано – Вейерштрасса о выделении сходящейся подпоследовательности из ограниченной последовательности
| Из любой ограниченной числовой последовательности можно выделить сходящуюся подпоследовательность:
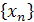 – огр. – огр.   ℝ ℝ
|
w Пусть последовательность 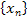 является ограниченной, т.е. является ограниченной, т.е.  при при  . .
Разделим отрезок  пополам точкой пополам точкой  ; при этом, по крайней мере, на одной половине окажется бесконечно много членов из ; при этом, по крайней мере, на одной половине окажется бесконечно много членов из 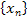 ; обозначим эту половину ; обозначим эту половину  и выберем на ней произвольно число и выберем на ней произвольно число  , где , где  , рис 22а): , рис 22а):
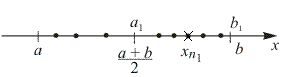
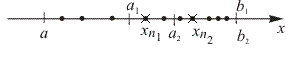
Рис. 22
Снова разделим  на две равные части и ту часть, в которую попадает бесконечно много членов из последовательности на две равные части и ту часть, в которую попадает бесконечно много членов из последовательности 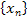 , обозначим , обозначим  . .
Поскольку на  находиться бесконечно много чисел из находиться бесконечно много чисел из 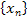 , то среди них есть члены с номерами заведомо большими, чем , то среди них есть члены с номерами заведомо большими, чем  . .
Выберем одно из таких чисел и обозначим его  , при этом , при этом  , рис 22б). , рис 22б).
Аналогично, разделив отрезок  пополам, выберем на одной из половинок пополам, выберем на одной из половинок
число  : :
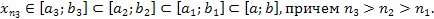
Продолжая этот процесс, в результате получится подпоследовательность из чисел
 , в которой номера , в которой номера  монотонно возрастают монотонно возрастают
с увеличением 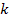 , при этом отрезки , при этом отрезки  будут вложенными, то есть будут вложенными, то есть

длины этих отрезков равны числам 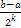 , которые очевидно стремятся к 0 при , которые очевидно стремятся к 0 при  . .
По свойству вложенных отрезков, длины, которых стремятся к нулю, получим, что эти отрезки имеют непустое пересечение, а точнее, что существует точка  при при  причем причем  . .
Так как последовательности  и и  являются монотонными и ограниченными, то по теореме Вейерштрасса из предыдущего параграфа заключаем, что являются монотонными и ограниченными, то по теореме Вейерштрасса из предыдущего параграфа заключаем, что
 и и  . .
Теперь рассматриваем этот факт вместе с двойным неравенством:
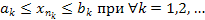
и по теореме о пределе зажатой последовательности делаем вывод, что  . .
Таким образом, построенная подпоследовательность 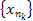 имеет конечный предел, т.е. является сходящейся. v имеет конечный предел, т.е. является сходящейся. v
Примеры (иллюстрация теоремы Больцано-Вейерштрасса)
1.  ; ;
эта последовательность ограниченная, так как  , но не сходящаяся; ее сходящиеся подпоследовательности имеют, например, следующий вид: , но не сходящаяся; ее сходящиеся подпоследовательности имеют, например, следующий вид:
 , где , где 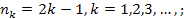
 , где , где 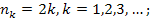
2.  ; ;
эта последовательность ограниченная, так как  , но не сходящаяся; , но не сходящаяся;
в этой последовательности бесконечно много раз встречаются числа

потому что 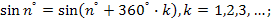
поэтому каждое указанное число является пределом подпоследовательности, в которой,
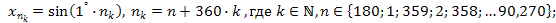
таким образом, если 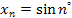 , то из этой ограниченной последовательности , то из этой ограниченной последовательности 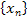 можно извлечь сходящиеся подпоследовательности можно извлечь сходящиеся подпоследовательности 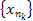 , количество которых равно числу 181. , количество которых равно числу 181.
Замечание
В дополнение к теореме Больцано-Вейерштрасса есть возможность доказать, что из любой неограниченной последовательности можно извлечь бесконечно большую подпоследовательность, имеющую своим пределом бесконечность определенного знака.
wДействительно, пусть последовательность 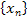 является неограниченной, потому что, например, неограниченна сверху. Тогда существует такой номер является неограниченной, потому что, например, неограниченна сверху. Тогда существует такой номер 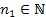 , что , что  . .
Поскольку последовательность 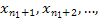 получающаяся из данной последовательности получающаяся из данной последовательности 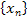 отбрасыванием конечного числа её членов отбрасыванием конечного числа её членов  также неограничена сверху, то найдется такой номер также неограничена сверху, то найдется такой номер  , что , что  , следовательно, , следовательно,  . Продолжая эти рассуждения, получаем последовательность таких номеров . Продолжая эти рассуждения, получаем последовательность таких номеров  , что , что  , и при этом , и при этом  . .
Таким образом, построена подпоследовательность 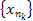 , которая монотонно возрастает и неограничена сверху, поэтому , которая монотонно возрастает и неограничена сверху, поэтому  , то есть , то есть 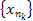 является бесконечно большой, имеющей своим пределом является бесконечно большой, имеющей своим пределом  . .
Аналогично приводится доказательство для случая, когда последовательность 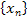 не является ограниченной снизу и тогда не является ограниченной снизу и тогда  , такая что , такая что 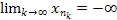 . v . v
Например, из неограниченной последовательности с
 извлекаются следующие бесконечно большие подпоследовательности: извлекаются следующие бесконечно большие подпоследовательности:
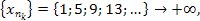
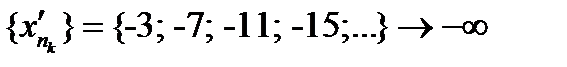
|
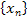 имеет конечный предел:
имеет конечный предел:  , то она является ограниченной. При этом обратное неверно, то есть не всякая ограниченная последовательность имеет предел. Например,
, то она является ограниченной. При этом обратное неверно, то есть не всякая ограниченная последовательность имеет предел. Например,  ограничена, но предела не имеет.
ограничена, но предела не имеет.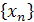 – огр.
– огр. 
 ℝ
ℝ
 при
при  .
. пополам точкой
пополам точкой  ; при этом, по крайней мере, на одной половине окажется бесконечно много членов из
; при этом, по крайней мере, на одной половине окажется бесконечно много членов из  и выберем на ней произвольно число
и выберем на ней произвольно число  , где
, где  , рис 22а):
, рис 22а):
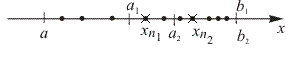
 .
. .
. , при этом
, при этом  , рис 22б).
, рис 22б). :
: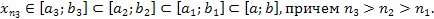
 , в которой номера
, в которой номера  монотонно возрастают
монотонно возрастают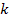 , при этом отрезки
, при этом отрезки  будут вложенными, то есть
будут вложенными, то есть
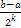 , которые очевидно стремятся к 0 при
, которые очевидно стремятся к 0 при  .
. при
при  причем
причем  .
. и
и  являются монотонными и ограниченными, то по теореме Вейерштрасса из предыдущего параграфа заключаем, что
являются монотонными и ограниченными, то по теореме Вейерштрасса из предыдущего параграфа заключаем, что и
и  .
.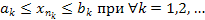
 .
.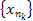 имеет конечный предел, т.е. является сходящейся. v
имеет конечный предел, т.е. является сходящейся. v ;
; , но не сходящаяся; ее сходящиеся подпоследовательности имеют, например, следующий вид:
, но не сходящаяся; ее сходящиеся подпоследовательности имеют, например, следующий вид: , где
, где 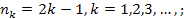
 , где
, где 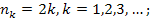
 ;
;
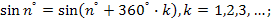
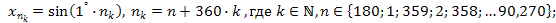
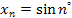 , то из этой ограниченной последовательности
, то из этой ограниченной последовательности 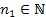 , что
, что  .
.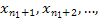 получающаяся из данной последовательности
получающаяся из данной последовательности  также неограничена сверху, то найдется такой номер
также неограничена сверху, то найдется такой номер  , следовательно,
, следовательно,  . Продолжая эти рассуждения, получаем последовательность таких номеров
. Продолжая эти рассуждения, получаем последовательность таких номеров  , и при этом
, и при этом  .
. , то есть
, то есть  .
. , такая что
, такая что 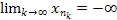 . v
. v извлекаются следующие бесконечно большие подпоследовательности:
извлекаются следующие бесконечно большие подпоследовательности: