Свойство локальной ограниченности функции, его связь с пределом Напомним, что функция  называется ограниченной на заданном множестве называется ограниченной на заданном множестве  , если является ограниченным множество её значений , если является ограниченным множество её значений
 , т.е. , т.е.  числа числа  и и  , такие что , такие что  . .
Часто используется другая форма записи факта ограниченности функции  на множестве на множестве  : :
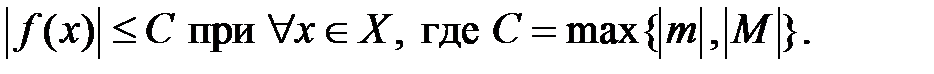
Например, 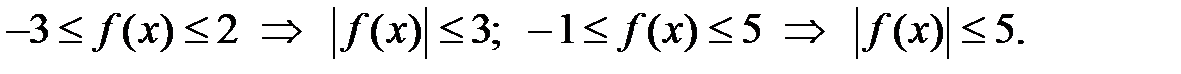
| Определение локальной ограниченности функции
| Функция  называется локально ограниченной в точке называется локально ограниченной в точке  (или при (или при  ), если можно указать такую окрестность точки ), если можно указать такую окрестность точки  , в которой функция , в которой функция  является ограниченной: является ограниченной:
 – лок. огр. в точке – лок. огр. в точке  при при  ℝ. ℝ.
|
Примеры (ограниченность на множестве и локальная ограниченность функций)
1)  – ограничена на всей ООФ, т.к. – ограничена на всей ООФ, т.к.  ℝ; является также локально ограниченной в любой точке ℝ; является также локально ограниченной в любой точке  ℝ и при ℝ и при 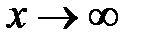 : :
2)  – является неограниченной на ООФ; – является неограниченной на ООФ;
в любой точке  , а также при , а также при  является локально ограниченной; является локально ограниченной;
в точке  является локально неограниченной: является локально неограниченной:

Связь понятий локальной ограниченности/неограниченности функции с её пределом устанавливается следующей ниже теоремой.
| Теорема о связи локальной ограниченности функции с её пределом
| 1. Если функция  имеет конечный предел в точке имеет конечный предел в точке  , то она является локально ограниченной в этой точке. , то она является локально ограниченной в этой точке.
|
w1. Пусть 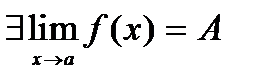 , где , где 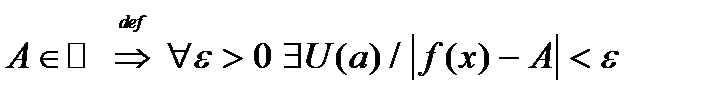 при при 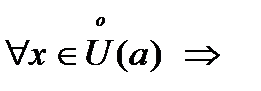
  , т.е. , т.е.  при при  , т.е. в проколотой окрестности точки , т.е. в проколотой окрестности точки  функция функция  является ограниченной; в самой точке является ограниченной; в самой точке  эта функция может быть не определена или может принимать некоторое числовое значение; таким образом, в полной окрестности точки эта функция может быть не определена или может принимать некоторое числовое значение; таким образом, в полной окрестности точки 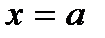 функция функция  имеет ограниченное множество значений, следовательно, является локально ограниченной.v имеет ограниченное множество значений, следовательно, является локально ограниченной.v
2. Если функция  имеет бесконечный предел в точке имеет бесконечный предел в точке  , то она является локально неограниченной в этой точке. , то она является локально неограниченной в этой точке.
|
w2. Пусть  при при 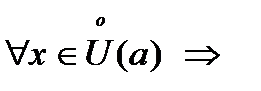
 при при  , т.е. в окрестности точки , т.е. в окрестности точки  множество значений функции является неограниченным. v множество значений функции является неограниченным. v
| Схема связи понятий предела и локальной ограниченности функции:
|  ℝ ℝ 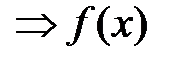 – локально ограниченная в точке – локально ограниченная в точке  ; ;
 – локально неограниченная в точке – локально неограниченная в точке 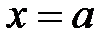 . .
|
Обратные следствия, вообще говоря, не являются справедливыми. В подтверждение этого приведем несколько примеров:
1)  – является локально ограниченной при – является локально ограниченной при  , но , но 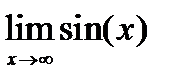 не не  ; ;
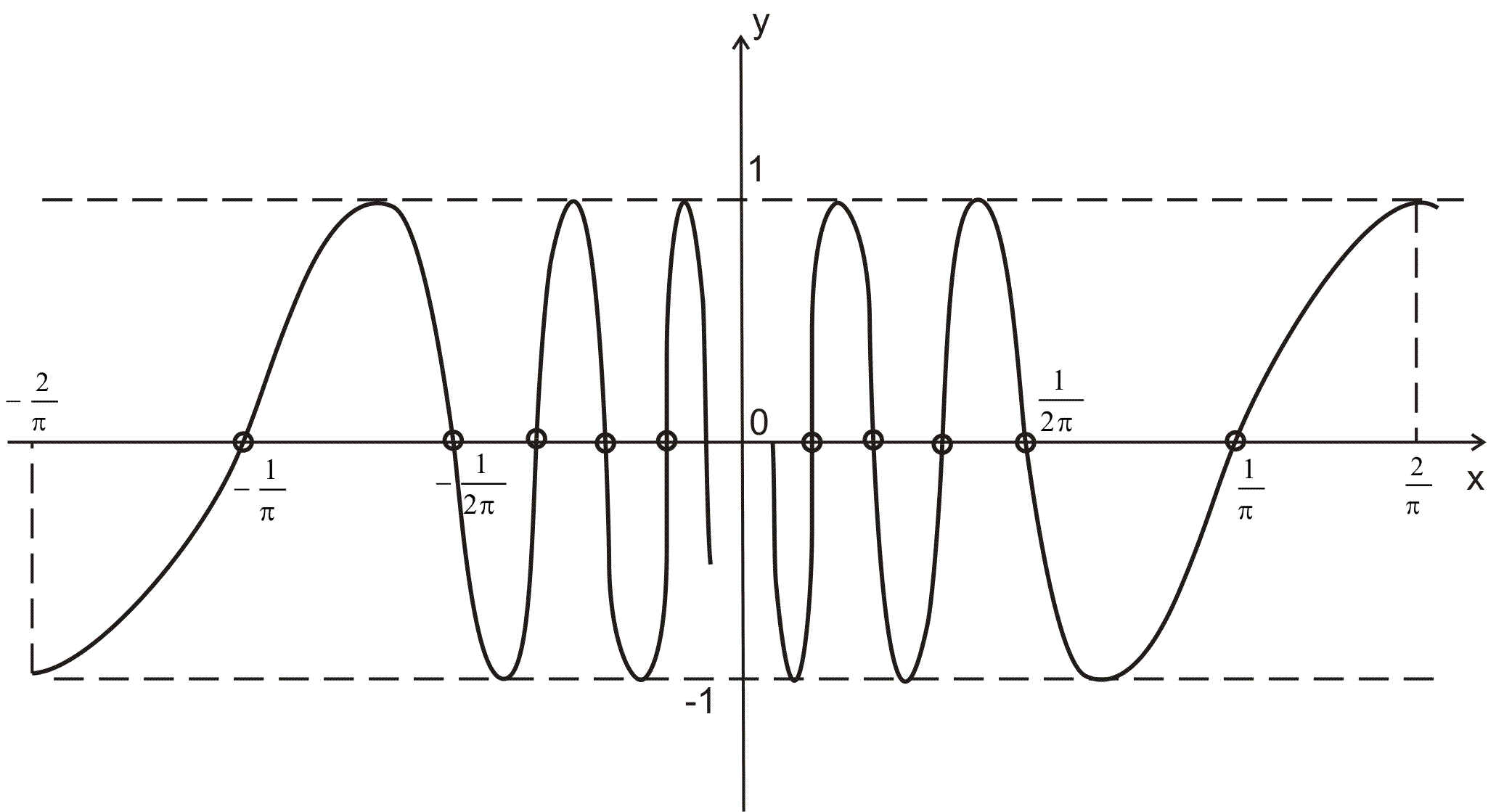
2)  – функция является ограниченной на всей ООФ и локально ограниченной при – функция является ограниченной на всей ООФ и локально ограниченной при  , но , но  не существует; не существует;
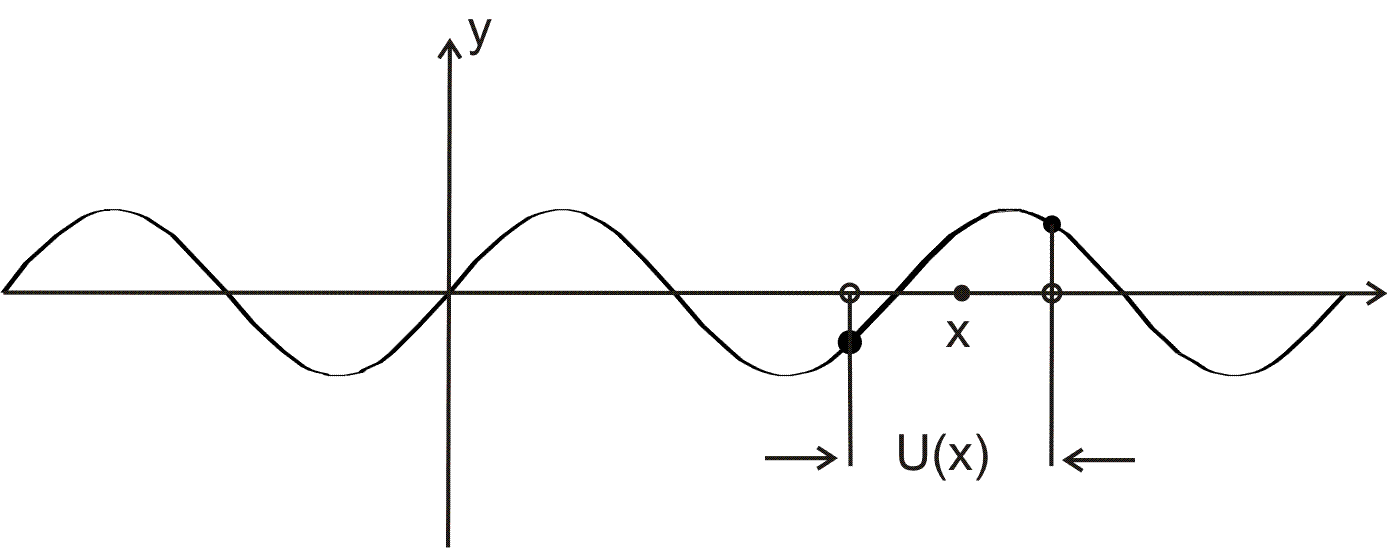
график  приведён на рисунке ниже: приведён на рисунке ниже:
3)  – функция является неограниченной при – функция является неограниченной при  , но не является бесконечно большой; , но не является бесконечно большой;
график четной функции  можно построить перемножением значений функций можно построить перемножением значений функций  и и  , его вид приведён на рисунке ниже: , его вид приведён на рисунке ниже:
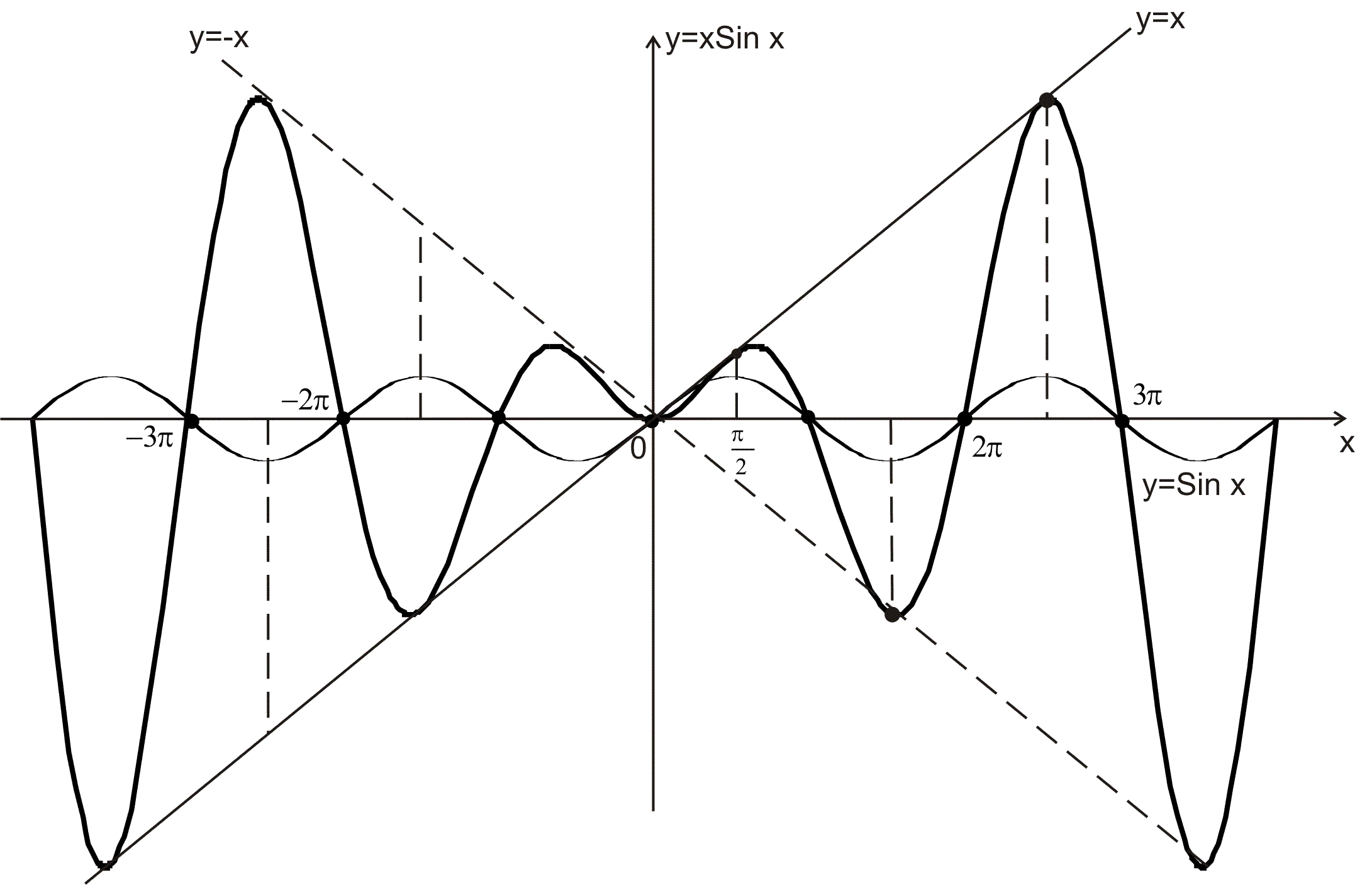
 не не  , т.к. не выполняется определение предела по Гейне: , т.к. не выполняется определение предела по Гейне:
для последовательности 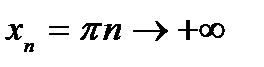 будет будет  , ,
для последовательности  будет будет 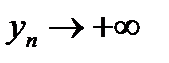 . .
На основании доказанной теоремы и рассмотренных примеров можно сделать следующие выводы:
1) Локальная ограниченность функции в точке  является необходимым, но не является достаточным условием для существования конечного является необходимым, но не является достаточным условием для существования конечного  ; ;
2) Локальная неограниченность функции в точке  является необходимым, но не является достаточным условием для существования бесконечного является необходимым, но не является достаточным условием для существования бесконечного  . .
3) Очевидно, что, если локальную ограниченность функции в точке  дополнить монотонностью при дополнить монотонностью при  слева или справа, то можно утверждать, что эта функция имеет конечный предел при слева или справа, то можно утверждать, что эта функция имеет конечный предел при  (по крайней мере, односторонний). (по крайней мере, односторонний).
Например,
Основные свойства бесконечно малых функций
1. Если  – бесконечно малая и – бесконечно малая и 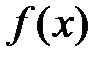 – локально ограниченная функции в точке – локально ограниченная функции в точке  , то их произведение , то их произведение 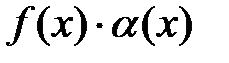 есть б.м. функция в той же точке есть б.м. функция в той же точке  . .
|
w  – лок. огр. в точке – лок. огр. в точке  число число  и и  ; ;
 – б.м. в точке – б.м. в точке 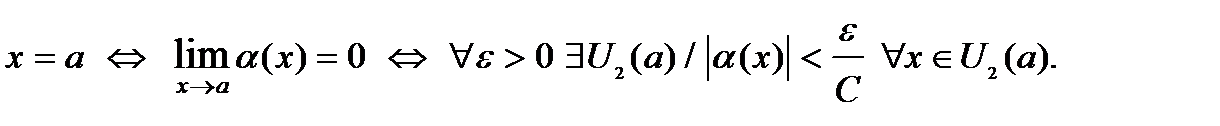
В окрестности точки  , которая является пересечением окрестностей , которая является пересечением окрестностей  и и  , рассмотрим произведение , рассмотрим произведение  : :
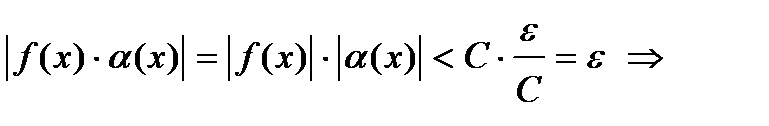
 при при 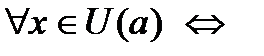
 – б.м. в точке – б.м. в точке  .v .v
2. Если две функции  и и  являются б.м. в одной и той же точке являются б.м. в одной и той же точке  , то их сумма , то их сумма  также является бесконечно малой. также является бесконечно малой.
|
w 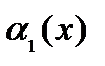 – б.м. при – б.м. при 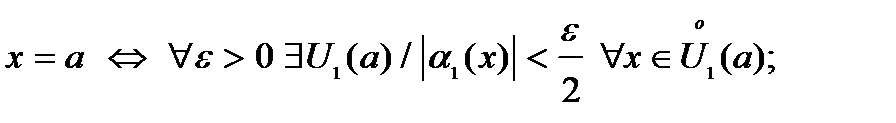
 – б.м. при – б.м. при  для того же для того же 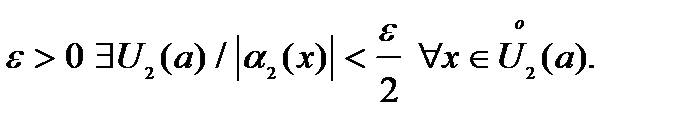
Для  имеем, что имеем, что 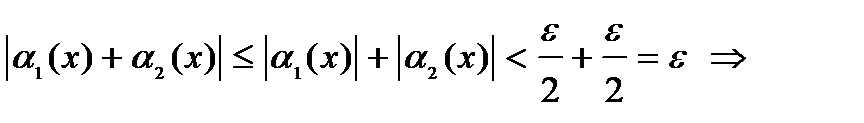
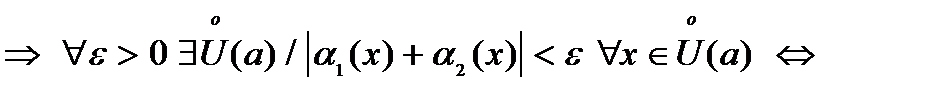
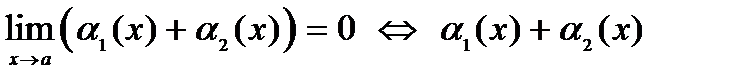 – б.м. при – б.м. при  .v .v
3. Если две функции  и и  являются б.м. в одной и той же точке являются б.м. в одной и той же точке  , то их произведение , то их произведение  также является бесконечно малой. также является бесконечно малой.
|
w 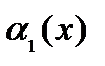 – б.м. в точке – б.м. в точке  является локально ограниченной в точке является локально ограниченной в точке  (как функция, имеющая конечный предел). Поэтому произведение локально ограниченной функции на б.м. является б.м. функцией при (как функция, имеющая конечный предел). Поэтому произведение локально ограниченной функции на б.м. является б.м. функцией при  (по свойству 1).v (по свойству 1).v
4. Если функция  – б.м. при – б.м. при  и и  в некоторой окрестности точки в некоторой окрестности точки  , то функция , то функция 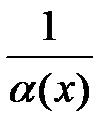 является б.б. при является б.б. при  . .
|
w 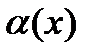 – б.м. при – б.м. при  . .
Если эту окрестность  пересечь с окрестностью точки пересечь с окрестностью точки  , в которой , в которой 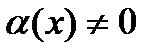 , и рассмотреть функцию , и рассмотреть функцию  , то получим, что , то получим, что 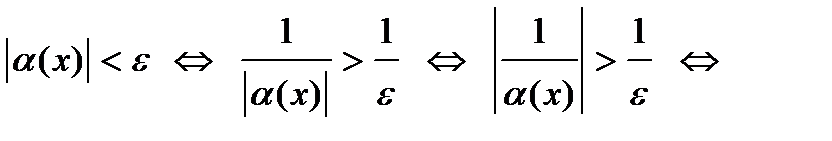
 – б.б. при – б.б. при  .v .v
|
 называется ограниченной на заданном множестве
называется ограниченной на заданном множестве  , если является ограниченным множество её значений
, если является ограниченным множество её значений , т.е.
, т.е.  числа
числа  и
и  , такие что
, такие что  .
. на множестве
на множестве  :
: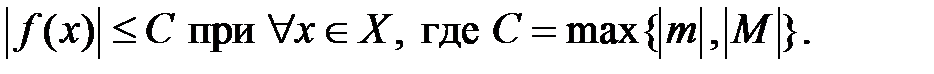
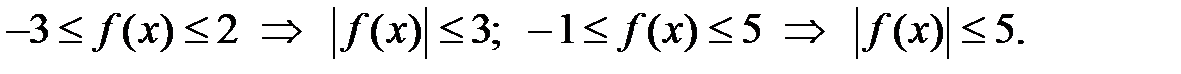
 называется локально ограниченной в точке
называется локально ограниченной в точке  (или при
(или при  ), если можно указать такую окрестность точки
), если можно указать такую окрестность точки  , в которой функция
, в которой функция  является ограниченной:
является ограниченной:
 – лок. огр. в точке
– лок. огр. в точке  при
при  ℝ.
ℝ.
 – ограничена на всей ООФ, т.к.
– ограничена на всей ООФ, т.к.  ℝ; является также локально ограниченной в любой точке
ℝ; является также локально ограниченной в любой точке  ℝ и при
ℝ и при 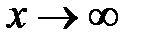 :
:
 – является неограниченной на ООФ;
– является неограниченной на ООФ; , а также при
, а также при  является локально ограниченной;
является локально ограниченной; является локально неограниченной:
является локально неограниченной:
 имеет конечный предел в точке
имеет конечный предел в точке  , то она является локально ограниченной в этой точке.
, то она является локально ограниченной в этой точке.
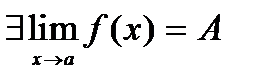 , где
, где 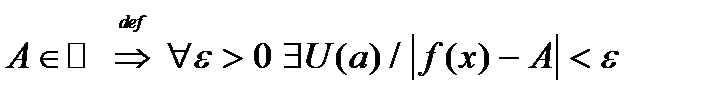 при
при 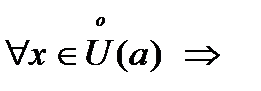

 , т.е.
, т.е.  при
при  , т.е. в проколотой окрестности точки
, т.е. в проколотой окрестности точки  функция
функция  является ограниченной; в самой точке
является ограниченной; в самой точке  эта функция может быть не определена или может принимать некоторое числовое значение; таким образом, в полной окрестности точки
эта функция может быть не определена или может принимать некоторое числовое значение; таким образом, в полной окрестности точки 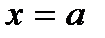 функция
функция  имеет ограниченное множество значений, следовательно, является локально ограниченной.v
имеет ограниченное множество значений, следовательно, является локально ограниченной.v при
при 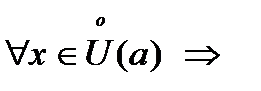
 при
при  , т.е. в окрестности точки
, т.е. в окрестности точки  множество значений функции является неограниченным. v
множество значений функции является неограниченным. v ℝ
ℝ 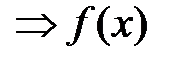 – локально ограниченная в точке
– локально ограниченная в точке  ;
;
 – локально неограниченная в точке
– локально неограниченная в точке 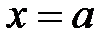 .
.
 – является локально ограниченной при
– является локально ограниченной при  , но
, но 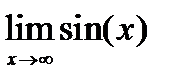 не
не  ;
; – функция является ограниченной на всей ООФ и локально ограниченной при
– функция является ограниченной на всей ООФ и локально ограниченной при  , но
, но  не существует;
не существует; приведён на рисунке ниже:
приведён на рисунке ниже:
 – функция является неограниченной при
– функция является неограниченной при  , но не является бесконечно большой;
, но не является бесконечно большой; можно построить перемножением значений функций
можно построить перемножением значений функций  и
и  , его вид приведён на рисунке ниже:
, его вид приведён на рисунке ниже:
 не
не  , т.к. не выполняется определение предела по Гейне:
, т.к. не выполняется определение предела по Гейне: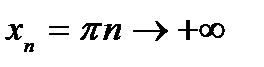 будет
будет  ,
, будет
будет 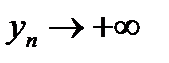 .
. является необходимым, но не является достаточным условием для существования конечного
является необходимым, но не является достаточным условием для существования конечного  ;
; является необходимым, но не является достаточным условием для существования бесконечного
является необходимым, но не является достаточным условием для существования бесконечного  .
. дополнить монотонностью при
дополнить монотонностью при  слева или справа, то можно утверждать, что эта функция имеет конечный предел при
слева или справа, то можно утверждать, что эта функция имеет конечный предел при  (по крайней мере, односторонний).
(по крайней мере, односторонний).
 и
и  ;
;
 – бесконечно малая и
– бесконечно малая и 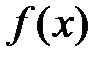 – локально ограниченная функции в точке
– локально ограниченная функции в точке  , то их произведение
, то их произведение 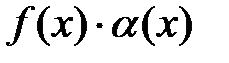 есть б.м. функция в той же точке
есть б.м. функция в той же точке  .
.
 – лок. огр. в точке
– лок. огр. в точке  число
число  и
и  ;
; – б.м. в точке
– б.м. в точке 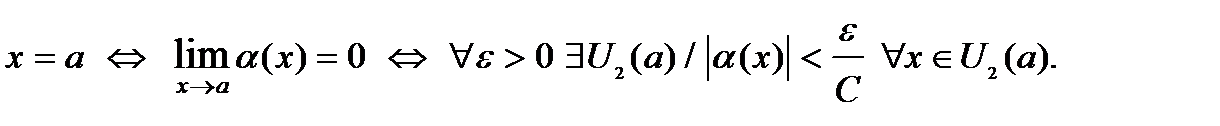
 , которая является пересечением окрестностей
, которая является пересечением окрестностей  и
и  , рассмотрим произведение
, рассмотрим произведение  :
: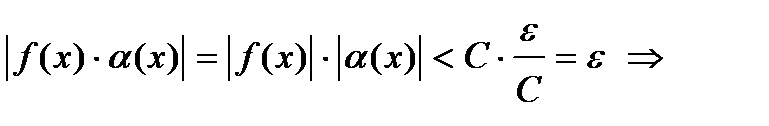
 при
при 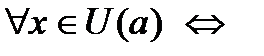
 – б.м. в точке
– б.м. в точке  .v
.v и
и  являются б.м. в одной и той же точке
являются б.м. в одной и той же точке  также является бесконечно малой.
также является бесконечно малой.
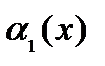 – б.м. при
– б.м. при 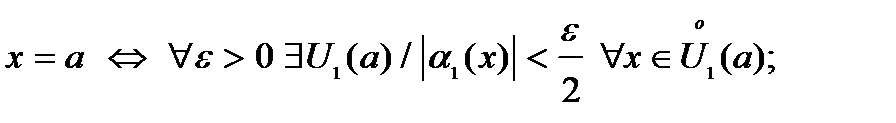
 – б.м. при
– б.м. при  для того же
для того же 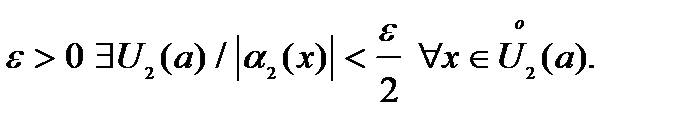
 имеем, что
имеем, что 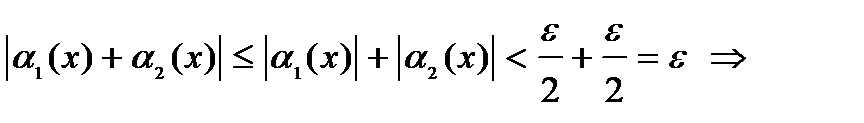
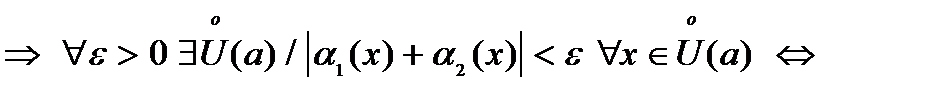
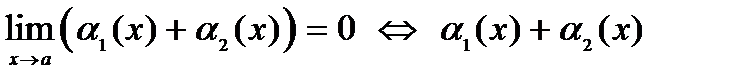 – б.м. при
– б.м. при  .v
.v также является бесконечно малой.
также является бесконечно малой.
 является локально ограниченной в точке
является локально ограниченной в точке  (как функция, имеющая конечный предел). Поэтому произведение локально ограниченной функции на б.м. является б.м. функцией при
(как функция, имеющая конечный предел). Поэтому произведение локально ограниченной функции на б.м. является б.м. функцией при  (по свойству 1).v
(по свойству 1).v – б.м. при
– б.м. при  и
и  в некоторой окрестности точки
в некоторой окрестности точки 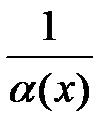 является б.б. при
является б.б. при 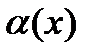 – б.м. при
– б.м. при  .
. пересечь с окрестностью точки
пересечь с окрестностью точки  , в которой
, в которой 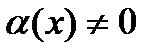 , и рассмотреть функцию
, и рассмотреть функцию  , то получим, что
, то получим, что 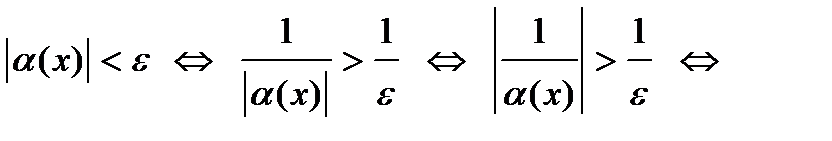
 – б.б. при
– б.б. при  .v
.v