|
|
Понятие фундаментальной последовательности. КритерийКоши. В этом пункте приводится важный критерий сходящейся последовательности, то есть необходимое и достаточное условие существования у неё конечного предела. При этом важность и оригинальность критерия состоит в том, что при его проверке не привлекается значение самого предела. В формулировке этого критерия и при работе с ним используется понятие фундаментальной последовательности.
Это условие называется условием Коши. Его можно записать еще в следующем виде:
Геометрическая интерпретация условия Коши состоит в том, что члены фундаментальной последовательности с достаточно большими номерами становятся сколь угодно близкими друг к другу, так как расстояние между любыми двумя членами этой последовательности меньше любого малого числа
wДоказательство необходимости. Пусть последовательность
Поэтому если брать
то есть
Доказательство достаточности. Пусть теперь последовательность 1 этап. Докажем, что Действительно, согласно условию Коши по
то есть часть последовательности 2 этап. Согласно теореме Больцано-Вейерштрасса из ограниченной последовательности
Докажем теперь, что число
Выберем теперь в подпоследовательности
то есть на основании условия Коши составлена оценка модуля разности между членами последовательности Рассматриваем
это означает, что существует конечный предел фундаментальной последовательности
Пример (доказательство сходимости последовательности по критерию Коши)
Пользуясь критерием Коши, докажем сходимость последовательности
для этого достаточно показать, что последовательность
Заметим, что это условие означает
и оценим
Далее используем для оценки последнего выражения очевидное неравенство
С учетом всех сделанных оценок получаем, что
Переходим к пределу в обеих частях этого неравенства при
но предел в левой части неравенства отрицательным быть не может, так как
Последовательность
5.5. Упражнения для самостоятельной работы Задача 1 Запишите последовательность 1) 3) Задача 2 Используя критерий Коши, докажите сходимость последовательностей
Ответы к упражнениям для самостоятельной работы
1)
2)
3)
4)
|
|
 называется фундаментальной последовательностью, если она удовлетворяет следующему условию: для любого числа
называется фундаментальной последовательностью, если она удовлетворяет следующему условию: для любого числа  существует такой номер
существует такой номер  , что для всех
, что для всех  и для всех
и для всех  выполняется неравенство
выполняется неравенство

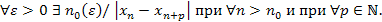
 , если номера этих членов больше, чем
, если номера этих членов больше, чем  .
.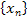 является сходящейся и имеет своим пределом число
является сходящейся и имеет своим пределом число 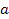 . Тогда по определению конечного предела имеем, что
. Тогда по определению конечного предела имеем, что
 и
и  , то
, то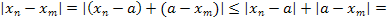
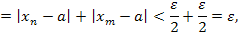
 при
при  и
и  , что и означает фундаментальность последовательности
, что и означает фундаментальность последовательности  . Таким образом, доказано, что если последовательность
. Таким образом, доказано, что если последовательность  можно указать такой номер
можно указать такой номер 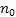 , что выполняется неравенство
, что выполняется неравенство  при
при  , тогда
, тогда
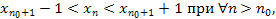
 является ограниченной. Поэтому очевидно, что является ограниченной и вся фундаментальная последовательность
является ограниченной. Поэтому очевидно, что является ограниченной и вся фундаментальная последовательность 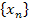 всегда можно извлечь сходящуюся подпоследовательность
всегда можно извлечь сходящуюся подпоследовательность  , так что
, так что  , где
, где  при
при  .
.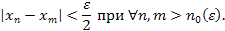
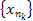 номера
номера 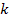 так, чтобы имело место неравенство
так, чтобы имело место неравенство  (это можно сделать в силу того, что
(это можно сделать в силу того, что  при
при  ). Тогда по условию Коши при
). Тогда по условию Коши при  имеем, что
имеем, что ,
, при
при  :
: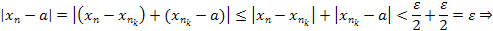
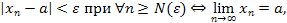
 сходится.v
сходится.v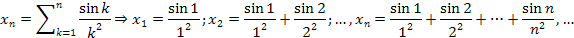

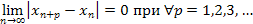
 для данной
для данной 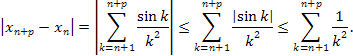
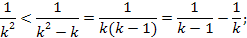
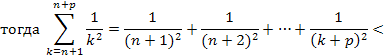
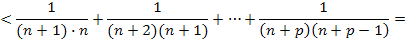
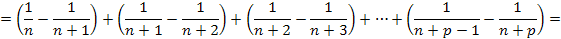
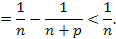

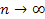 :
: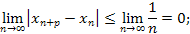
 ; поэтому остается сделать вывод, что
; поэтому остается сделать вывод, что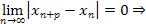
 , выделите из неё сходящуюся подпоследовательность, если
, выделите из неё сходящуюся подпоследовательность, если  ; 2)
; 2)  ;
; ; 4)
; 4)  .
.

 .
. - ограничена т.к.
- ограничена т.к.  при
при 
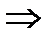
 ,
,  ,
,  ;
; - неограничена
- неограничена  ;
; - ограничена, т.к.
- ограничена, т.к. 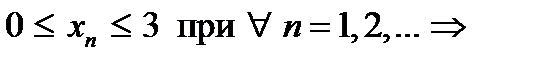
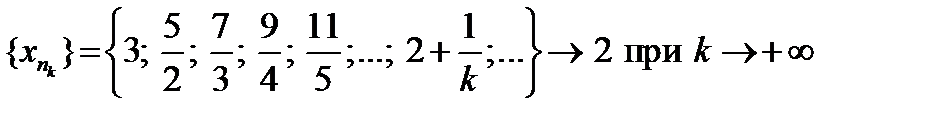 ;
; ;
; - неограниченная, но не бесконечно большая
- неограниченная, но не бесконечно большая 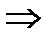
 ,
, 
 при
при  .
.