Обратная связь
|
Предел функции: различные определения
6.1. Определение предела функции на языке последовательностей (по Гейне) 50
6.2. Точка сгущения множества 52
6.3. Определение предела функции по заданному множеству. 55
6.4. Определение предела функции на языке окрестностей (по Коши) 56
6.5. Записи определения предела функции на языке «ε-δ». 60
6.6. Дополнительные детали определения предела функции. 63
6.7. Примеры доказательства пределов функции 65
6.8. Упражнения для самостоятельной работы 69
§ 1
§ 2
§ 3
§ 4
§ 5
§ 6
Определение предела функции на языке последовательностей (по Гейне)
Рассмотрим функцию y=f(x): X→ Y, где X   , Y , Y   . .
Пусть зафиксированы точки x=a и y=A расширенного множества  . .
| Определение предела функции на языке последовательностей, или по Гейне
|
Точка А называется пределом значений функции y=f(x) в точке x=a, если для любой последовательности значений аргумента  , имеющей своим пределом точку а, последовательность соответствующих значений функции , имеющей своим пределом точку а, последовательность соответствующих значений функции  имеет своим пределом точку A. имеет своим пределом точку A.
 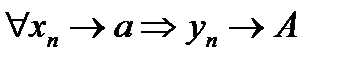 , где , где  ℕ. ℕ.
|
Другое обозначение предела функции: 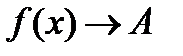 при при  . .
| Примеры иллюстраций к определению предела функции на языке последовательностей приведены на следующих ниже рисунках.
|
Рис.21
Если  ℝ, то есть A является числом, то говорят, что функция y=f(x) в точке x=a имеет конечный предел, равный А. ℝ, то есть A является числом, то говорят, что функция y=f(x) в точке x=a имеет конечный предел, равный А.
Если 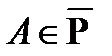 и является одним из символов и является одним из символов  , то говорят, что функция y=f(x) в точке x=a имеет бесконечный предел; в этом случае функция f(x) называется бесконечно большой в точке x=a (или в окрестности точки x=a). , то говорят, что функция y=f(x) в точке x=a имеет бесконечный предел; в этом случае функция f(x) называется бесконечно большой в точке x=a (или в окрестности точки x=a).
Сформулированное определение предела функции y=f(x),  содержательно только тогда, когда для точки x=a существуют последовательности точек содержательно только тогда, когда для точки x=a существуют последовательности точек  , такие что , такие что  . Чтобы гарантировать это существование, вводится понятие точки сгущения множества X, на котором задана функция f(x). . Чтобы гарантировать это существование, вводится понятие точки сгущения множества X, на котором задана функция f(x).
Точка сгущения множества
| Определение точки сгущения множества, или точки прикосновения множества
| |
Точка а называется точкой сгущения множества Х, если в любой окрестности этой точки содержатся точки из множества Х, отличные от точки а.
|
При этом сама точка сгущения может как входить в множество Х, так и не входить.
Например, пусть Х=[a;b] или Х=(a;b). В обоих случаях точка х=а является точкой сгущения для множества Х, так как в любой ее окрестности содержатся точки из Х, отличные от точки а. Иллюстрации этого факта приведены на рисунках 25-25.
Аналогично точкой сгущения для множества Х в обоих случаях является любая точка с, такая что a<c<b. Таким образом, для обоих случаев множества Х в этом примере его точками сгущения являются любые точки 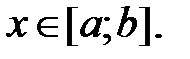
В предположении, что х=а есть точка сгущения для множества Х, можно всегда из этого множества извлечь последовательность  , сходящуюся к точке а. Алгоритм реализации этого утверждения дается в доказательстве следующей теоремы. , сходящуюся к точке а. Алгоритм реализации этого утверждения дается в доказательстве следующей теоремы.
| Теорема (о существовании последовательности, сходящейся к точке сгущения)
| |
Если точка x=a является точкой сгущения множества Х, то всегда из этого множества можно выделить последовательность {xn}, имеющую своим пределом точку x=a.
|
w Для доказательства достаточно рассмотреть такие ε-окрестности точки а, в которых  , n=1,2,3, … . В каждой из этих окрестностей будут находиться точки из множества Х, отличные от а (в соответствии с определением точки сгущения). Далее на рисунках показан процесс выбора элементов x1, x2, x3, … , xn, … для случаев, когда , n=1,2,3, … . В каждой из этих окрестностей будут находиться точки из множества Х, отличные от а (в соответствии с определением точки сгущения). Далее на рисунках показан процесс выбора элементов x1, x2, x3, … , xn, … для случаев, когда  ℝ или a=+∞. ℝ или a=+∞.
Если 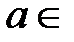 ℝ, то выбирая ℝ, то выбирая 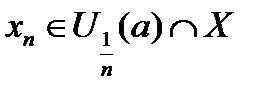 , но , но  , получим последовательность точек , получим последовательность точек  , сходящуюся к точке а: , сходящуюся к точке а:
 . .
Если  , то числа , то числа  будут образовывать бесконечно большую последовательность: будут образовывать бесконечно большую последовательность:
 . .
Таким образом, если а – это точка сгущения множества Х, то всегда из условия  следует, что следует, что  . v . v
Далее в определении предела функции  всегда предполагается, что х=а является точкой сгущения множества задания функции f(x). всегда предполагается, что х=а является точкой сгущения множества задания функции f(x).
|
|

 , Y
, Y  , имеющей своим пределом точку а, последовательность соответствующих значений функции
, имеющей своим пределом точку а, последовательность соответствующих значений функции  имеет своим пределом точку A.
имеет своим пределом точку A.

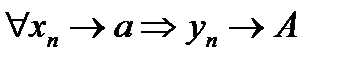 , где
, где  ℕ.
ℕ.
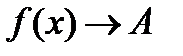 при
при  .
. ℝ,
y=A
ℝ,
y=A  ℝ,
ℝ,




 ,
,
 ℝ,
ℝ,



 ℝ,
ℝ,
 ,
,
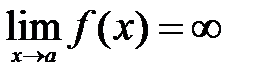


 ,
,
 ,
,

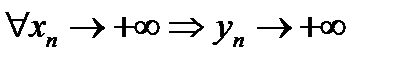
 ℝ, то есть A является числом, то говорят, что функция y=f(x) в точке x=a имеет конечный предел, равный А.
ℝ, то есть A является числом, то говорят, что функция y=f(x) в точке x=a имеет конечный предел, равный А.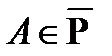 и является одним из символов
и является одним из символов  , то говорят, что функция y=f(x) в точке x=a имеет бесконечный предел; в этом случае функция f(x) называется бесконечно большой в точке x=a (или в окрестности точки x=a).
, то говорят, что функция y=f(x) в точке x=a имеет бесконечный предел; в этом случае функция f(x) называется бесконечно большой в точке x=a (или в окрестности точки x=a). содержательно только тогда, когда для точки x=a существуют последовательности точек
содержательно только тогда, когда для точки x=a существуют последовательности точек  , такие что
, такие что  . Чтобы гарантировать это существование, вводится понятие точки сгущения множества X, на котором задана функция f(x).
. Чтобы гарантировать это существование, вводится понятие точки сгущения множества X, на котором задана функция f(x).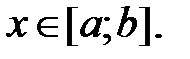
 , сходящуюся к точке а. Алгоритм реализации этого утверждения дается в доказательстве следующей теоремы.
, сходящуюся к точке а. Алгоритм реализации этого утверждения дается в доказательстве следующей теоремы. , n=1,2,3, … . В каждой из этих окрестностей будут находиться точки из множества Х, отличные от а (в соответствии с определением точки сгущения). Далее на рисунках показан процесс выбора элементов x1, x2, x3, … , xn, … для случаев, когда
, n=1,2,3, … . В каждой из этих окрестностей будут находиться точки из множества Х, отличные от а (в соответствии с определением точки сгущения). Далее на рисунках показан процесс выбора элементов x1, x2, x3, … , xn, … для случаев, когда  ℝ или a=+∞.
ℝ или a=+∞.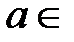 ℝ, то выбирая
ℝ, то выбирая 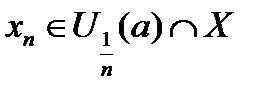 , но
, но  , получим последовательность точек
, получим последовательность точек  , сходящуюся к точке а:
, сходящуюся к точке а: .
. , то числа
, то числа  будут образовывать бесконечно большую последовательность:
будут образовывать бесконечно большую последовательность: .
. следует, что
следует, что  . v
. v всегда предполагается, что х=а является точкой сгущения множества задания функции f(x).
всегда предполагается, что х=а является точкой сгущения множества задания функции f(x).