|
|
Модуль I. Кинематика материальной точки.1.1. Занятие 1. Кинематика материальной точки. Векторный и координатный способы задания движения. Скорость и ускорение. Движение с постоянным ускорением. Краткие теоретические сведения Основные формулы Кинематические уравнения движения
Средняя скорость
Средняя путевая скорость
Мгновенная скорость
Проекции скорости
Модуль скорости
Мгновенное ускорение
Проекции ускорения на оси координат
Модуль ускорения
Уравнение равномерного движения
Уравнение равнопеременного движения
“+” – равноускоренное движение; “-” – равнозамедленное движение. Движение тела вертикально вверх
где g=9,81м/с2- ускорение свободного падения у поверхности Земли, Движение тела вертикально вниз
Вопросы для ответа у доски: 1. Векторный способ описания движения. Скорость и ускорение. Покажите, что задание векторной функции 2. Координатный способ описания движения. Скорость и ускорение. Связь между векторным и координатным способами описания движения. Дайте понятие о системе координат и перечислите наиболее часто употребляемые системы. Покажите, что задание кинематических уравнений достаточно для описания движения точки в пространстве. Укажите роль начальных условий. Получите выражения для проекций скорости и ускорения на соответствующие оси координат. Найдите модуль скорости и ускорения и направление соответствующих векторов в любой точке траектории. Рассмотрите конкретный пример: как по заданным кинематическим уравнениям определить траекторию движущейся точки, проекции вектора скорости и ускорения, их модули и углы, составляемые векторами 3. Прямолинейное движение с постоянным ускорением. Рассмотрите случай прямолинейного движения с постоянным ускорением. Получите формулы для скорости и координаты точки, движущейся с постоянным ускорением, и покажите их зависимость от времени на графиках. Могут ли быть изломы на этих графиках? Какие характеристики движения можно получить из этих графиков? Как вычислить путь, пройденный точкой за некоторое время? В каких единицах измеряются скорость и ускорение? Дайте определение единиц. 4. Движение тела, брошенного вертикально вверх. Получите формулы скорости и высоты (координаты) подъема тела в зависимости от времени, а также максимальную высоту и время подъема на нее. Покажите, что время подъема равно времени падения тела. Для рассматриваемого движения изобразите на графиках ускорение, скорость, координату и путь, пройденный телом, в зависимости от времени. Примеры решения задач: Задача 1. Уравнение движения материальной точки имеет вид Решение: Средняя скорость равна:
Среднее ускорение равно:
Мгновенную скорость находим из уравнения:
отсюда
Подставляя эти выражения в уравнение для среднего ускорения, получим:
Значит, ускорение точки при заданном законе движения постоянно, что с очевидностью получается из уравнения движения, поскольку ускорение (его мгновенное значение) может быть получено дифференцированием уравнения движения, что дает именно такой результат:
Ответ: Задача 2. Два тела начали одновременно двигаться равноускоренно: одно с начальной скоростью 5 м/с и ускорением 1,5 м/с2, а другое без начальной скорости с ускорением 2,5 м/с2. Построить графики их движений и по графикам определить, через сколько времени оба тела будут иметь одинаковую скорость и какой путь пройдет каждое тело за это время. Решение: При равноускоренном движении скорости первого и второго тел равны:
Подставив значения
Строим графики скоростей движения тел. Графики скоростей (Рис.1.1.1) пересекаются при
Запишем уравнение равноускоренного движения: откуда уравнения движения для обоих тел:
Для первого и второго тел пройденные пути за
Рис.1.1.1 Ответ: Задача 3. Свободно падающее тело в последнюю секунду движения проходит половину всего пути. Найти с какой высоты Решение: Разобьем весь участок движения на два: верхний и нижний (Рис.1.1.2). Составим для каждого из них уравнение движения.
Учитывая, что получим:
Время падения равно:
Так как время движения на всем участке больше времени движения на нижнем участке, то:
Подставив числовые данные, получим высоту, с которой падает тело, равную:
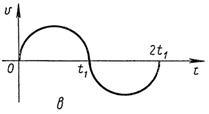
Ответ: Вопросы для самопроверки: 1. Что изучается в разделе механики “Кинематика”? 2. Что называется механическим движением? 3. Что такое система отсчета? 4. Для чего необходимы эталоны длины и времени и как они устанавливаются? 5. Что называют скаляром и вектором? Приведите примеры скалярных и векторных величин в механике. 6. Какие операции с векторами вы знаете? 7. Что такое векторная функция скалярного аргумента? Как находить производные по времени от векторных функций? 8. Покажите на рисунке 9. Покажите на рисунке 10. Какое движение называют равномерным, неравномерным равнопеременным? 11. Что называют скоростью равномерного прямолинейного движения? Почему величина скорости равномерного движения не зависит от длительности промежутка времени, за который она вычисляется? 12. Как вычислить среднюю скорость произвольного движения точки? В каком случае для вычисления средней скорости можно воспользоваться формулой 13. Упругий шар падает с высоты Задачи для самостоятельного решения: 1. Тело брошено вертикально вверх с начальной скоростью 4м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью вертикально вверх брошено второе тело. На каком расстоянии от начального пункта встретятся тела? Сопротивление воздуха не учитывать. 2. Материальная точка движется прямолинейно с начальной скоростью 10м/с и постоянным ускорением 5м/с2. Определить, во сколько раз путь, пройденный материальной точкой, будет превышать модуль ее перемещения спустя 4с после начала отсчета времени. 3. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью 18км/ч. Далее половину оставшегося времени он ехал со скоростью 22км/ч, после чего до конечного пункта он шел пешком со скоростью 5км/ч. Определить среднюю скорость велосипедиста. 4. Три лодки стоят в спокойной воде на одинаковом расстоянии друг от друга в вершинах равностороннего треугольника. Лодки начинают двигаться с постоянной по величине скоростью 5. Прямолинейное движение точки описывается уравнением 6. Скорость точки при прямолинейном движении с течением времени изменяется по закону, представленному на Рис.1.1.3. Участки кривых на Рис.1.1.3б являются участками парабол, на Рис.1.1.3в – дугой окружности. Постройте графики зависимостей:
Рис.1.1.3 7. Мяч брошен вертикально вверх с начальной скоростью 8. По идеально гладкой плоскости, составляющей угол 9. С аэростата, находящегося на высоте 10. Тело падает с высоты 11. Зависимость пройденного пути 12. Зависимость пройденного телом пути 13. Все звезды, в частности некоторая звезда 14. Кабина лифта, у которой расстояние от пола до потолка 2,7 м, начала подниматься с ускорением 1,2 м/с2. Через 2с после начала подъема с потолка кабины стал падать болт. Найти: а) время свободного падения болта; б) перемещение и путь болта за время свободного падения в системе отсчета, связанной с шахтой лифта. 15. Радиус-вектор частицы меняется со временем 16. В момент времени 17. Точка движется в плоскости 18. Человек находится на расстоянии 19. Наблюдатель, стоящий в момент начала движения электропоезда у его переднего края, заметил, что первый вагон прошел мимо него за 20. Наблюдатель, стоящий на платформе, заметил, что первый вагон электропоезда, приближающегося к станции, прошел мимо него в течение 4с, а второй – в течение 5с. После этого передний край поезда остановился на расстоянии 75 м от наблюдателя. Считая движение поезда равномерно замедленным, определить его ускорение. 21. От пристани А вверх и вниз по реке отправляются два одинаковых катера и прибывают к пристаням В и С через одинаковые отрезки времени. Обратное возвращение катера из В в А требует в 1,5 раза больше времени, чем возвращение второго катера из С в А. Во сколько раз скорость катера в стоячей воде больше скорости течения реки? 1.2. Занятие 2. Кинематика материальной точки. Криволинейное движение и естественный способ задания движения. Краткие теоретические сведения Основные формулы Ускорение при криволинейном движении (по дуге окружности)
где Модули ускорений
Вопросы для ответа у доски: 1. Естественный способ описания движения. Скорость. Вычисление пути, пройденного телом. Изложите сущность естественного способа описания движения. Закон движения и пройденный путь. Классификация движений по виду траектории и характеру движения. Получите выражение для скорости при данном способе описания движения. Приведите пример вычисления криволинейной координаты и пройденного пути по заданной скорости. 2. Ускорение при криволинейном движении. Нормальное и тангенциальное ускорения. Получите выражение для ускорения при криволинейном движении в векторной форме. Выясните физический смысл тангенциального и нормального ускорений. Покажите на рисунке расположение векторов 3. Криволинейное движение с постоянным ускорением: 1) движение тела, брошенного горизонтально; 2) движение тела, брошенного под углом к горизонту. Выведите формулы для проекций скоростей, величины скорости и координат падающего тела в зависимости от времени. Изобразите полученные функции на графиках. Найдите выражение для дальности и времени полета, а также скорости в момент падения тела на землю. Примеры решения задач: Задача 1. Точка движется по кривой с постоянным тангенциальным ускорением
Ответ: Задача 2. Камень брошен горизонтально со скоростью Решение: Выполним чертеж (Рис.1.2.2). Нормальное ускорение камня:
где
 , ,
После подстановки в уравнение (1) скорости
Вычисляя, находим:
Ответ: Задача 3. С башни высотой Решение: Движение тела, брошенного с высоты Высота подъема тела
Расстояние от основания башни до места падения камня на землю:
Скорость, с которой камень упадет на землю:
Вычисляя, находим Угол отсюда Ответ: Вопросы для самопроверки: 1. Приведите примеры, показывающие относительность понятия траектории. 2. Сколько координат требуется при естественном способе описания движения? 3. При каком условии естественная координата (расстояние) совпадает с пройденным путем; не совпадает? 4. Что называют средней и мгновенной скоростью криволинейного движения? Как по скорости определить направление движения на траектории? 5. Что определяет первая производная от пути по времени; от естественной координаты по времени? Совпадают ли результаты их вычисления? 6. Отличаются ли графики зависимости пути и естественной координаты от времени для одного и того же движения? 7. Как находится производная по времени от вектора постоянной длины? 8. Дайте определение векторного произведения двух векторов (модуля, направления) и запишите его выражение в декартовой системе координат. 9. Что такое естественный трехгранник? 10. Как определяются кривизна и радиус кривизны кривой? 11. Движение задано в координатной или векторной форме. Как найти 12. При каком условии тело будет двигаться: 1) равномерно и прямолинейно? 2) ускоренно (замедленно) и прямолинейно? 3) равномерно и криволинейно? 4) ускоренно (замедленно) и криволинейно? Показать на рисунках. 13. Что означает утверждение, что криволинейное движение - ускоренное движение? 14. Как перейти от векторного или координатного способа к естественному и наоборот? 15. В чем заключается принцип независимости движений? 16. Изобразите на графиках зависимость координат, проекций скоростей, модуля скорости в зависимости от времени для тела, брошенного горизонтально. 17. То же самое для тела, брошенного под углом к горизонту. Задачи для самостоятельного решения: 1. Тело брошено под углом 300 к горизонту со скоростью 30 м/с. Каковы будут нормальное и тангенциальное ускорения тела через время 1 с после начала движения? 2. Материальная точка движется по окружности с постоянной угловой скоростью 3. Камень, брошенный горизонтально на высоте 4. Дальность полета тела, брошенного под углом к горизонту, равна 5. Аэростат поднимается вертикально вверх со скоростью 6. На идеально гладкую наклонную плоскость, составляющую с горизонтом угол 7. Автомобиль начал двигаться по выпуклому мосту со скоростью 8. Камень, брошенный горизонтально, упал на землю через время 9. Камень брошен горизонтально со скоростью 10. Тело брошено со скоростью 11. Тело брошено со скоростью 12. Тело брошено со скоростью 13. Два шарика бросили одновременно из одной точки в горизонтальном направлении в противоположные стороны со скоростями 14. Частица движется в плоскости 15. Пушка и цель находятся на одном уровне на расстоянии 5,1 км друг от друга. Через сколько времени снаряд с начальной скоростью 240 м/с достигнет цели? 16. Воздушный шар начинает подниматься с поверхности земли. Скорость его подъема постоянна и равна |
|
 где
где  время.
время. где
где  перемещение материальной точки за время
перемещение материальной точки за время 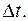
 где
где  путь, пройденный материальной точкой за время
путь, пройденный материальной точкой за время  где
где  радиус-вектор.
радиус-вектор. на оси координат
на оси координат 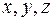
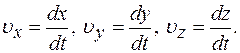
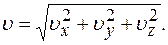
 где
где 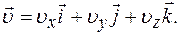
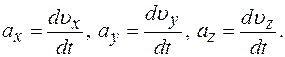
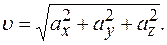
 равномерное движение.
равномерное движение.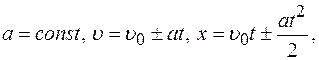
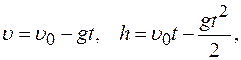
 высота подъема.
высота подъема.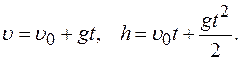
 полностью описывает движение материальной точки в пространстве. Введите в рассмотрение понятия перемещения, средней и мгновенной скорости, среднего и мгновенного ускорения. Ответы проиллюстрируйте соответствующими рисунками. Приведите конкретный пример зависимости радиус-вектора от времени и вычислите скорость и ускорение точки. В заключение необходимо отметить достоинства и недостатки векторного способа описания движения.
полностью описывает движение материальной точки в пространстве. Введите в рассмотрение понятия перемещения, средней и мгновенной скорости, среднего и мгновенного ускорения. Ответы проиллюстрируйте соответствующими рисунками. Приведите конкретный пример зависимости радиус-вектора от времени и вычислите скорость и ускорение точки. В заключение необходимо отметить достоинства и недостатки векторного способа описания движения. с координатными осями. В заключение покажите переход от координатного способа описания движения к векторному и наоборот. Укажите достоинства и недостатки координатного метода.
с координатными осями. В заключение покажите переход от координатного способа описания движения к векторному и наоборот. Укажите достоинства и недостатки координатного метода. , где
, где 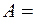 2 м/с,
2 м/с, 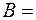 -2 м/с2. Определите среднее значение скорости, и ускорения в интервале времени от 2 до 4 с.
-2 м/с2. Определите среднее значение скорости, и ускорения в интервале времени от 2 до 4 с.

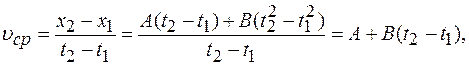
 0,8 м/с.
0,8 м/с. .
.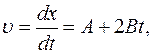
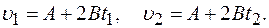
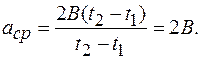
 -0,4 м/с2.
-0,4 м/с2. -0,4 м/с2.
-0,4 м/с2.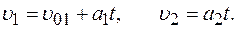
 и
и 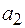 , получим:
, получим: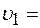 5+1,5
5+1,5 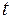 (м/с),
(м/с), 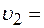 2,5
2,5  5+1,5
5+1,5  5 с.
5 с.
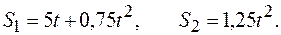
 Графики движений тел построены на Рис.1.1.1
Графики движений тел построены на Рис.1.1.1 м;
м;  м.
м. 43,75 м;
43,75 м;  31,25 м.
31,25 м. падает тело и время
падает тело и время  Так как начальная скорость для верхнего и всего участка по условию задачи равна нулю, то запишем уравнения движения для всего участка и верхнего участка.
Так как начальная скорость для верхнего и всего участка по условию задачи равна нулю, то запишем уравнения движения для всего участка и верхнего участка.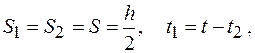
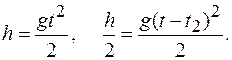
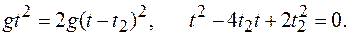
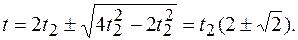

 29,07 м.
29,07 м.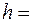 29,07 м.
29,07 м. и
и  . В каком случае
. В каком случае 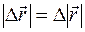 ?
? и
и  .
. ?
? так, что в каждый момент времени одна лодка находится на курсе другой. Найдите: а) уравнение траектории движения лодок и место их встречи; б) время, через которое встретятся лодки, и расстояние, пройденное каждой из них до встречи.
так, что в каждый момент времени одна лодка находится на курсе другой. Найдите: а) уравнение траектории движения лодок и место их встречи; б) время, через которое встретятся лодки, и расстояние, пройденное каждой из них до встречи. (м). а) Запишите уравнение скорости и ускорения точки. б) Сколько времени движется точка до остановки? в) Определите максимальную скорость точки. г) Чему равна средняя скорость точки за время движения до остановки? д) Через сколько времени средняя скорость достигнет максимального значения и какова ее величина?
(м). а) Запишите уравнение скорости и ускорения точки. б) Сколько времени движется точка до остановки? в) Определите максимальную скорость точки. г) Чему равна средняя скорость точки за время движения до остановки? д) Через сколько времени средняя скорость достигнет максимального значения и какова ее величина?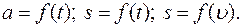


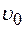 . Через сколько времени нужно бросить вверх второй мяч, чтобы они встретились в наикратчайшее время, если известно, что начальная скорость второго мяча вдвое меньше, чем у первого? На какой высоте встретятся мячи?
. Через сколько времени нужно бросить вверх второй мяч, чтобы они встретились в наикратчайшее время, если известно, что начальная скорость второго мяча вдвое меньше, чем у первого? На какой высоте встретятся мячи? 300 с горизонтом, пустили снизу вверх шайбу. На расстоянии большем
300 с горизонтом, пустили снизу вверх шайбу. На расстоянии большем  1,0 м от основания плоскости шайба находилась время
1,0 м от основания плоскости шайба находилась время  0,5с. Найдите начальную скорость шайбы и пройденный ею путь по наклонной плоскости.
0,5с. Найдите начальную скорость шайбы и пройденный ею путь по наклонной плоскости.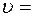 5м/с; б) аэростат опускается со скоростью
5м/с; б) аэростат опускается со скоростью 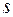 от времени
от времени  где
где 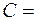 4м/с3. Найти: а) зависимость скорости
4м/с3. Найти: а) зависимость скорости 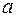 от времени
от времени  пройденное телом, скорость
пройденное телом, скорость  3 через 0,5 с.
3 через 0,5 с. где
где  0,01 м/с3. Через какое время
0,01 м/с3. Через какое время 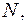 удаляются от Солнца со скоростями, пропорциональными их расстоянию до него. Как будет выглядеть эта картина с “точки зрения” звезды
удаляются от Солнца со скоростями, пропорциональными их расстоянию до него. Как будет выглядеть эта картина с “точки зрения” звезды 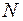 ?
? где
где  постоянный вектор,
постоянный вектор,  положительная постоянная. Найти: а) скорость и ускорение частицы как функции
положительная постоянная. Найти: а) скорость и ускорение частицы как функции 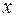 . Ее скорость меняется со временем
. Ее скорость меняется со временем  где
где  начальная скорость, ее модуль
начальная скорость, ее модуль  10,0 см/с,
10,0 см/с, 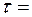 5,0 с. Найти: а) координату
5,0 с. Найти: а) координату 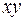 по закону:
по закону:  где
где  и
и  положительные постоянные. Найти: а) уравнение траектории точки
положительные постоянные. Найти: а) уравнение траектории точки  и ее график; б) модули скорости и ускорения точки как функции
и ее график; б) модули скорости и ускорения точки как функции  между векторами
между векторами 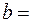 200м от человека и если человек может бежать со скоростью
200м от человека и если человек может бежать со скоростью 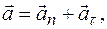
 нормальное ускорение, направленное по радиусу к центру окружности;
нормальное ускорение, направленное по радиусу к центру окружности;  тангенциальное ускорение, направленное по касательной к точке окружности.
тангенциальное ускорение, направленное по касательной к точке окружности. радиус окружности.
радиус окружности. при ускоренном и замедленном движении.
при ускоренном и замедленном движении. 0,5 м/с2. Определить полное ускорение точки на участке кривой с радиусом кривизны
0,5 м/с2. Определить полное ускорение точки на участке кривой с радиусом кривизны 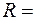 3 м, если точка движется на этом участке со скоростью
3 м, если точка движется на этом участке со скоростью 
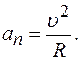 Полное ускорение точки равно:
Полное ускорение точки равно:
 Подставив числовые значения, получим:
Подставив числовые значения, получим:
 0,8 м/с2.
0,8 м/с2.
 10 м/с. Найти радиус кривизны
10 м/с. Найти радиус кривизны  траектории камня через время
траектории камня через время  Отсюда радиус кривизны траектории камня:
Отсюда радиус кривизны траектории камня: (1)
(1)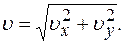
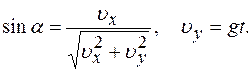
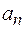 получим:
получим: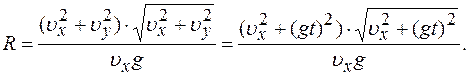
 305 м.
305 м. 25 м брошен камень со скоростью
25 м брошен камень со скоростью  от основания башни он упадет на землю? С какой скоростью
от основания башни он упадет на землю? С какой скоростью  под углом
под углом 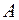 и движение тела, брошенного из точки
и движение тела, брошенного из точки 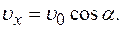
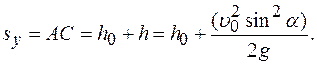
 Общее время движения камня
Общее время движения камня  где
где  время подъема камня на высоту
время подъема камня на высоту  время падения камня.
время падения камня. 27,9 м;
27,9 м;  0,77 с;
0,77 с; 2,39 с;
2,39 с;  где
где  10 м,
10 м, 31,1 м; отсюда
31,1 м; отсюда  где
где 
 ,
,  23,4 м/с.
23,4 м/с. 26,7 м/с.
26,7 м/с. составляемый траекторией камня с горизонтом в точке падения камня на землю, найдется из формулы
составляемый траекторией камня с горизонтом в точке падения камня на землю, найдется из формулы 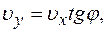
 1,8;
1,8; 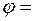 610.
610.
 и
и  рад/с. Во сколько раз путь, пройденный точкой за время 4с, будет больше модуля ее перемещения? Принять, что в момент начала отсчета времени радиус-вектор
рад/с. Во сколько раз путь, пройденный точкой за время 4с, будет больше модуля ее перемещения? Принять, что в момент начала отсчета времени радиус-вектор 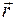 , задающий положение точки на окружности, относительно исходного положения был повернут на угол
, задающий положение точки на окружности, относительно исходного положения был повернут на угол  3 рад.
3 рад. 10 м от точки бросания. Найдите: а) начальную скорость камня; б) уравнение траектории и угол падения; в) нормальное и тангенциальное ускорение камня через время
10 м от точки бросания. Найдите: а) начальную скорость камня; б) уравнение траектории и угол падения; в) нормальное и тангенциальное ускорение камня через время 
 из него в горизонтальном направлении бросили предмет со скоростью
из него в горизонтальном направлении бросили предмет со скоростью  Определите расстояние между точками первого и второго удара при условии, что плоскость: а) покоится; б) поднимается вертикально вверх со скоростью
Определите расстояние между точками первого и второго удара при условии, что плоскость: а) покоится; б) поднимается вертикально вверх со скоростью 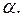
 изменяющейся в зависимости от пройденного расстояния по закону
изменяющейся в зависимости от пройденного расстояния по закону  Каково ускорение автомобиля в тот момент, когда он опишет по мосту дугу в
Каково ускорение автомобиля в тот момент, когда он опишет по мосту дугу в  он брошен? С какой скоростью он упадет на землю? Какой угол
он брошен? С какой скоростью он упадет на землю? Какой угол 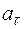 ускорения камня через время
ускорения камня через время  если известно, что высота подъема тела
если известно, что высота подъема тела  противоположным положительному направлению оси
противоположным положительному направлению оси  Уравнение траектории частицы имеет вид
Уравнение траектории частицы имеет вид  где
где  Благодаря ветру шар приобретает горизонтальную компоненту скорости
Благодаря ветру шар приобретает горизонтальную компоненту скорости  , где
, где  высота подъема. Найти: а) сноса шара
высота подъема. Найти: а) сноса шара  ; б) полного, тангенциального и нормального ускорений шара.
; б) полного, тангенциального и нормального ускорений шара.