|
|
Модуль 3. статика. Механика жидкостей и газов. Механические колебания и волны.Занятие 1. Статика. Краткие теоретические сведения Основные формулы Относительный покой и движение точки с постоянной скоростью можно рассматривать как частный случай переменного движения, при котором ее ускорение равно нулю. Из основного уравнения динамики:
Для равновесия материальной точки необходимо, чтобы геометрическая сумма всех сил, приложенных к точке, равнялась нулю. Уравнения равновесия материальной точки в проекциях:
Равновесие твердого тела зависит не только от модуля и направления действующих сил, но и от точки приложения. Механическое состояние абсолютно твердого тела не изменяется, если точку приложения действующей на него силу переносить вдоль линии ее действия. Равнодействующая двух или нескольких сил, приложенных к телу под углом друг к другу, равна их векторной сумме и находится по правилу параллелограмма. Две параллельные силы могут быть уравновешены одной силой. Уравновешивающая сила параллельна им, и ее модуль равен алгебраической сумме модулей слагаемых сил:
Линия действия уравновешивающей силы отстоит от линии действия силы
где Мерой взаимодействия тел, при котором происходит деформация или изменение угловой скорости вращения тел, служит момент силы. Модуль момента силы
Момент силы, стремящийся повернуть тело относительно точки При действии на тело нескольких сил, расположенных в одной плоскости (плоская система сил), модуль результирующего момента этих сил относительно выбранной точки
Условия равновесия тела:
Координаты центра тяжести системы материальных точек на плоскости:
 масса масса  й частицы; й частицы;  координата координата  й частицы; й частицы;  масса всех частиц. масса всех частиц.
Задача 1. Выкладывая карниз из камня, каменщик кладет один на другой четыре кирпича так, что часть вышестоящего кирпича выступает над нижележащим (Рис.3.1.1а). Длина каждого кирпича равна Решение: Так как кирпичи однородны, то центр тяжести каждого кирпича находится на середине его длины. Вследствие этого самый верхний кирпич будет находиться в равновесии по отношению к лежащему под ним, если его центр тяжести лежит на продолжении линии среза второго кирпича, т.е. наибольшая длина свеса первого кирпича Центр тяжести первого и второго кирпичей, взятых вместе, будет расположен на расстоянии Относительно правого верхнего края самого нижнего кирпича два самых верхних кирпича будут создавать вращательный момент Третий кирпич от верха будет создавать вращательный момент противоположного знака, равный Запишем условие равновесия: Отсюда Наибольшие выступающие части равны: верхнего первого кирпича - Ответ: Задача 2. Пять шаров, массы которых равны соответственно Решение: Система будет находиться в равновесии, если в центре ее тяжести приложить уравновешенную силу
 Пусть массы тел системы равны Пусть массы тел системы равны  и положение центра тяжести будем отсчитывать по горизонтали (ось и положение центра тяжести будем отсчитывать по горизонтали (ось  ) от центра тяжести крайнего левого шара (Рис.3.1.2а). Тогда расстояние от точки ) от центра тяжести крайнего левого шара (Рис.3.1.2а). Тогда расстояние от точки  до линии действия уравновешивающей силы – координату до линии действия уравновешивающей силы – координату  центра тяжести системы можно найти из уравнения моментов, составленного относительно точки центра тяжести системы можно найти из уравнения моментов, составленного относительно точки  : :
где
или где
 в центре первого шара и на произвольном расстоянии в центре первого шара и на произвольном расстоянии 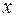 мысленно прикладываем к стержню уравновешивающую силу мысленно прикладываем к стержню уравновешивающую силу  , модуль которой равен модулю силы тяжести, действующей на всю систему: , модуль которой равен модулю силы тяжести, действующей на всю систему:
Находим плечи всех сил относительно точки Подставляем в уравнение (1) и определяем положение центра тяжести:
Ответ: Задача 3. Определите положение центра тяжести однородной квадратной пластинки со стороной Решение: Рассмотрим, как определяется положение центра тяжести однородной плоской фигуры, имеющей вырез.
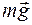 , можно представить как сумму двух параллельных сил – силы тяжести вырезанной части (диска), равной , можно представить как сумму двух параллельных сил – силы тяжести вырезанной части (диска), равной  , и силы тяжести оставшейся фигуры (квадрата с отверстием), равной , и силы тяжести оставшейся фигуры (квадрата с отверстием), равной  . .
Первая из этих сил приложена в центре тяжести невырезанной фигуры (квадрата), вторая – в центре тяжести вырезанной части (круга), третья – в неизвестном пока центре пластинки с отверстием. Так как известны: равнодействующая сила (
так как модуль силы тяжести оставшейся части фигуры равен
Из равенства (1) находим:
поскольку масса однородной пластинки одинаковой толщины
где Площадь вырезанной части Расстояние между центрами тяжести вырезанного диска и квадрата равно:
Подставляя в равенство (2) найденные значения, находим центр тяжести фигуры:
Ответ: Вопросы и задания для самопроверки 1. Дайте определение равнодействующей и уравновешивающей сил. 2. Чему равна равнодействующая двух параллельных сил, направленных в одну сторону; в противоположные стороны? Где находится ее точка приложения? 3. Чему равна равнодействующая двух непараллельных сил? Как найти ее точку приложения? 4. Что такое пара сил? Как определяется момент пары? Как будет двигаться свободное тело, на которое действует пара сил? 5. Что называется связями? Как определяются реакции связей? Приведите примеры. 6. Каким условиям должны удовлетворять силы, действующие на тело, находящееся в равновесии? 7. Сформулируйте условия устойчивого, неустойчивого и безразличного равновесия. Как связаны эти условия с запасом потенциальной энергии? 8. Можно ли строго горизонтально натянуть трос? 9. На столе лежит катушка ниток. Как надо тянуть за нить, чтобы катушка катилась вперед; назад; скользила по столу? Сделайте чертеж. 10. Как легче сдвинуть с места железнодорожный вагон: прилагая силу к корпусу вагона или к верхней части обода колеса? 11. Почему при резком трогании с места автомобиль обязательно “приседает” на задние колеса, а при резком торможении обязательно “клюет” носом? 12. На веревочной петле в горизонтальном положении висит стержень. Нарушится ли равновесие, если стержень с одной стороны согнуть? 13. В цилиндрический стакан наливают воду. При каком уровне воды в стакане центр тяжести стакана с водой занимает наинизшее положение? 14. Кирпич лежит на наклонной плоскости. Какая половина кирпича (верхняя или нижняя) оказывает большее давление на наклонную плоскость? 15. По лестнице, прислоненной к гладкой вертикальной стене, поднимается человек. Лестница начинает скользить лишь тогда, когда человек поднимается на определенную высоту. Почему? Задачи для самостоятельного решения 1. Фонарь весом 200 Н подвешен на тросе над серединой улицы, ширина которой 10 м. Трос разрывается под действием силы 1000 Н. На какой высоте нужно укрепить концы троса, чтобы он не разорвался, если фонарь должен находиться на высоте 6 м? 2. На балку, лежащую на двух опорах А и В, нужно положить груз массой 1500 кг. Длина балки 7 м. На каком расстоянии от опоры А нужно расположить груз, чтобы на опору А он давил с силой 5000Н? 3. Из однородного плоского диска радиусом 1,2 м вырезали круг вдвое меньшего диаметра, центр которого лежит на середине радиуса. На каком расстоянии от центра диска находится центр тяжести получившейся фигуры? 4. У стены стоит лестница. Коэффициент трения лестницы о стену 5. На плоской поверхности, образующей с горизонтом угол 200, лежит доска, в верхнюю сторону которой вбит гвоздь, проходящий сквозь ее центр тяжести. Коэффициент статического трения доски по наклонной поверхности равен 0,4. Масса доски равна 0,5 кг. Определить максимальную силу, с которой можно надавить на гвоздь, не вызывая движения доски, в следующих случаях: а) сила параллельна поверхности, образует с горизонтом угол 200 и направлена вверх; б) сила противоположна этому направлению; в) сила горизонтальна и образует с наклонной поверхностью угол 200. 6.
 Между двумя гвоздями натянут шнур длиной 1,7 м. Расстояние между гвоздями равно 1,5 м. На шнур повешен груз весом 200 Н (Рис.3.1.4). Определить натяжение шнура, пренебрегая изменением длины шнура при навешивании груза. Между двумя гвоздями натянут шнур длиной 1,7 м. Расстояние между гвоздями равно 1,5 м. На шнур повешен груз весом 200 Н (Рис.3.1.4). Определить натяжение шнура, пренебрегая изменением длины шнура при навешивании груза.
7.
 Шар, масса которого равна 5 кг, опирается на две гладкие ( Шар, масса которого равна 5 кг, опирается на две гладкие ( 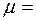 0) плоскости, образующие угол, причем левая образует с горизонтом угол 0) плоскости, образующие угол, причем левая образует с горизонтом угол  350, а правая – угол 350, а правая – угол 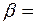 200 (Рис.3.1.5). Определить силы, с которыми шар давит на плоскости. 200 (Рис.3.1.5). Определить силы, с которыми шар давит на плоскости.
8.
9.
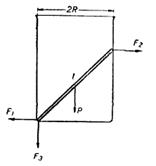 В гладкий цилиндрический стакан помещена палочка, как показано на Рис.3.1.7. Длина палочки В гладкий цилиндрический стакан помещена палочка, как показано на Рис.3.1.7. Длина палочки 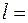 15 см; масса 15 см; масса  30 г. С какими силами действует палочка на дно и стенки стакана, если радиус дна стакана 30 г. С какими силами действует палочка на дно и стенки стакана, если радиус дна стакана 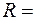 7см? Трением пренебречь. 7см? Трением пренебречь.
10.
 Тонкий стержень длиной Тонкий стержень длиной 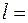 100 см, сделанный из дерева плотностью 100 см, сделанный из дерева плотностью  0,8 г/см3, подвешенный за один из концов, а другим погружен в воду. Определить угол 0,8 г/см3, подвешенный за один из концов, а другим погружен в воду. Определить угол  между направлением стержня и вертикалью, если верхний конец находится над уровнем воды на высоте между направлением стержня и вертикалью, если верхний конец находится над уровнем воды на высоте  , равной: а) 30см; б) 70 см. , равной: а) 30см; б) 70 см.
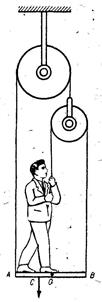
11. 12. Человек весом 60 кг стоит на балке весом 30 кг, подвешенной на блоках (Рис.3.1.9). Длина балки между точками опоры 3 м. Определить, какую силу должен приложить человек и в каком месте он должен встать, чтобы балка находилась в равновесии и занимала горизонтальное положение. 13.

14. На деревянном полу стоит маленькая лестница. Посредине она связана веревкой. Веревка разрывается под действием на нее силы 10 кг. Определить, при каком угле при вершине лестнице веревка разорвется, если на верхней ступени лестницы стоит человек весом 70 кг (коэффициент трения о дерево 0,65). Вес лестницы не учитывать. 15.
 Диск массой 5 кг находится на шероховатой наклонной планке, образующей с горизонтом угол 200 (Рис.3.1.11). Качение диска предотвращено трением и горизонтально расположенной веревкой, которая одним своим концом прикреплена к самой верхней точке диска Диск массой 5 кг находится на шероховатой наклонной планке, образующей с горизонтом угол 200 (Рис.3.1.11). Качение диска предотвращено трением и горизонтально расположенной веревкой, которая одним своим концом прикреплена к самой верхней точке диска 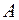 , а другим – к планке. Определить натяжение веревки, когда диск неподвижен. , а другим – к планке. Определить натяжение веревки, когда диск неподвижен.
16. Три одинаковых цилиндра уложены так, как показано на Рис.3.1.12. При каких условиях они будут удерживаться в этом положении неподвижно? 17.
 и массой и массой  . Тот рабочий, который идет впереди, держит бревно на расстоянии . Тот рабочий, который идет впереди, держит бревно на расстоянии  от конца бревна, а тот, который идет позади, держит бревно за другой конец. Найти силы давления, испытываемые каждым рабочим со стороны бревна. от конца бревна, а тот, который идет позади, держит бревно за другой конец. Найти силы давления, испытываемые каждым рабочим со стороны бревна.
18. К концам стержня массой 19. На наклонной плоскости стоит кубик. Каким должен быть угол 20. Однородный стержень согнут под прямым углом и подвешен за один конец. Под каким углом |
|
 0 и
0 и  , если
, если  0.
0. 0 и
0 и  0.
0.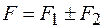 .
. на расстоянии:
на расстоянии: ,
,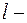 расстояние между линиями действия приложенных сил. Знак ‘+” берется, когда силы направлены в одну сторону, знак “-“ – в противоположные.
расстояние между линиями действия приложенных сил. Знак ‘+” берется, когда силы направлены в одну сторону, знак “-“ – в противоположные. .
. .
. 0.
0. ;
;  ,
, Примеры решения задач:
Примеры решения задач: Рис.3.1.1б.
Рис.3.1.1б. 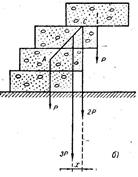
 .
.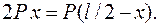
 /6, т.е. третий кирпич может выступать над четвертым не более чем на 1/6 своей длины.
/6, т.е. третий кирпич может выступать над четвертым не более чем на 1/6 своей длины.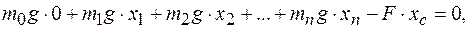
 плечи сил;
плечи сил;  относительно центра тяжести левого шара. Подставляя в это уравнение, вместо модуля уравновешивающей силы, его выражение
относительно центра тяжести левого шара. Подставляя в это уравнение, вместо модуля уравновешивающей силы, его выражение  и, решая уравнение относительно
и, решая уравнение относительно 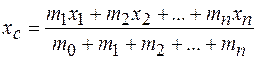
 (1)
(1)
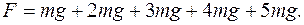
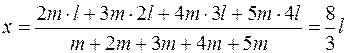
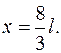
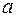 , в которой вырезано круглое отверстие радиусом
, в которой вырезано круглое отверстие радиусом  Положение центра тяжести целой фигуры и центра тяжести вырезанной части известно. Фигуру с вырезом изобразим так, чтобы ось симметрии была горизонтальна.
Положение центра тяжести целой фигуры и центра тяжести вырезанной части известно. Фигуру с вырезом изобразим так, чтобы ось симметрии была горизонтальна.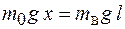 или
или  , (1)
, (1)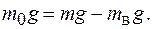
 , (2)
, (2)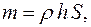
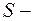 площадь;
площадь;  плотность материала.
плотность материала.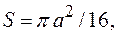 площадь всей фигуры (квадрата):
площадь всей фигуры (квадрата): 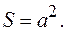
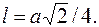
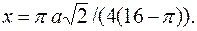
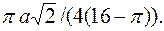
 0,4, лестницы о землю —
0,4, лестницы о землю —  0,5. Определить наименьший угол, который может образовывать лестница с полом, не соскальзывая.
0,5. Определить наименьший угол, который может образовывать лестница с полом, не соскальзывая.
 Из однородной круглой пластинки радиусом 18 см вырезан круг вдвое меньшего радиуса, касающийся края первого круга (Рис.3.1.8). Найти центр тяжести полученной пластинки.
Из однородной круглой пластинки радиусом 18 см вырезан круг вдвое меньшего радиуса, касающийся края первого круга (Рис.3.1.8). Найти центр тяжести полученной пластинки.
 40 кг и
40 кг и  10 кг. Где надо подпереть стержень, чтобы он находился в равновесии?
10 кг. Где надо подпереть стержень, чтобы он находился в равновесии?