|
|
Занятие 2. Механика жидкостей и газов.Краткие теоретические сведения Основные формулы Давление жидкости. Поверхностные явления. Внутреннее трение в жидкости. 1. Расход жидкости в трубке тока: объемный расход:
массовый расход:
где 2. Уравнение неразрывности струи:
где
3. Уравнение Бернулли:
4. Скорость течения жидкости из малого отверстия в открытом широком сосуде:
где 5. Поверхностное натяжение:
где 6. Формула Лапласа, выражающая давление
где 7. Высота подъема жидкости в капиллярной трубке определяется по формуле Жюрена:
где 8. Высота подъема жидкости между двумя близкими и параллельными плоскостями:
где 9. Объем жидкости (газа), протекающей за время
где 10. Число Рейнольдса для потока жидкости в длинных трубках
где 11. Число Рейнольдса для движения шарика в жидкости:
где 12. Сила сопротивления
где Вопросы для ответа у доски: 1. Вывод уравнения Бернулли для идеальной жидкости. Используя закон сохранения энергии, получите уравнение Бернулли. Выясните физический смысл каждого слагаемого, входящего в уравнение. Укажите условия, при которых можно использовать уравнение Бернулли. 2. Следствия из уравнения Бернулли. Рассмотрите следствия из уравнения Бернулли: а) найти скорость истечения жидкости из небольшого отверстия в широком сосуде, т.е. получить формулу Торричелли; б) найти силу, с которой вытекающая жидкость действует на сосуд, т.е. определить реакцию вытекающей струи; в) привести примеры технического использования уравнения Бернулли - приборы для измерения давления и скоростей в жидкостях, водоструйные насосы, гидравлические турбины, реактивное движение и др. 3. Движение вязкой жидкости. Объясните возникновение внутреннего трения в жидкостях и газах и приведите формулу Ньютона для сил трения. Установите физический смысл коэффициента вязкости и единицы измерения этого коэффициента. Получите выражение для скорости течения вязкой жидкости по цилиндрической трубе. 4. Вывод формулы Пуазейля. Вычислите поток жидкости (объем жидкости, протекающей за единицу времени через поперечное сечение трубы), т. е. получите формулу Пуазейля и проанализируйте ее. Дайте определение ламинарного и турбулентного течения жидкости и введите число Рейнольдса. Укажите, при каких условиях применима формула Пуазейля. Примеры решения задач: Задача 1. Льдина плавает в море, выдаваясь на 250 м3 над поверхностью. Определите объем всей льдины, если плотность воды 1030 кг/м3, а льда 900 кг/м3.
Объем всей льдины складывается из объема надводной части
Сила тяжести льдины равна:
Сила Архимеда действует только на подводную часть льдины:
Находим объем подводной части льдины из уравнения (2):
тогда Сила Архимеда:
Приравнивая (5) и (3), получим:
Произведя вычисления, получаем:
Ответ: 1981 м3. Задача 2. В сосуд льется вода, за время, равное 1 с, наливается объем воды 0,2л. Каким должен быть диаметр
Отсюда Тогда скорость вытекания воды:
Приравняв левую и правую части, получим:
отсюда диаметр отверстия в дне сосуда:
Проверим размерность:
Подставив числовые данные, находим:
Ответ: 1,4 см. Задача 3. Какой наибольшей скорости Решение: Так как силу Архимеда можно не учитывать, то во время падения на каплю действуют две противоположно направленные силы: сила тяжести
По закону Стокса:
приравняв левую и правую части, получим:
Масса капли:
где
отсюда:
Проверим размерность:
Подставив числовые данные, находим максимальную скорость капли:
Ответ: 4,1 м/с. Вопросы для самопроверки: 1. Что общего между жидкостью и газом? Что их различает? Чем отличаются механические свойства жидкостей и газов от свойств твердого тела? 2. При каких видах деформаций газ и жидкость проявляют упругие свойства? 3. Чем отличается условие равновесия жидкости от условия равновесия твердого тела? 4. В чем заключается закон Паскаля? 5. Как найти давление в покоящихся жидкостях и газах? Оцените массу атмосферы Земли. 6. В чем заключается закон Архимеда? Какова величина силы Архимеда, где она приложена и как направлена? 7. Условия плавания тел. Почему тонущий корабль, погрузившись в воду, часто опрокидывается? 8. В стакане с водой плавает кусок льда. Как изменится уровень воды в стакане, когда лед растает? Что изменится, если кусок льда содержит полость; если во льду находится кусок железа? 9. Два сплошных тела из одного и того же вещества подвешены к концам неравно плечного рычага и уравновешивают друг друга в воздухе. Сохранится ли равновесие, если погрузить эти тела в сосуд с водой? Изменится ли равновесие, если тела имеют различную плотность? 10. Каковы особенности изучения движения жидкости по сравнению с твердыми телами (ведь и те и другие - системы материальных точек)? 11. Какое движение жидкости называется установившимся? Что такое линия тока? Почему в установившемся движении линии тока и траектория движения частицы совпадают? 12. Что называется трубкой тока? Могут ли частицы пересекать поверхность трубки тока? Почему? 13. Что такое идеальная и реальная жидкости? Какое движение жидкости называют ламинарным, турбулентным? При каком условии одно движение переходит в другое? 14. Какой вид имеет уравнение неразрывности для сжимаемой и несжимаемой жидкостей? 15. Применимо ли уравнение Бернулли к турбулентному течению жидкости? 16. Как образуется лобовое сопротивление? 17. Как происходит обтекание воздухом крыла самолета? Чем объясняется появление подъемной силы крыла? Какую роль играют завихрения, образующиеся за кромкой крыла? 18. Может ли образоваться подъемная сила в идеальной жидкости? Какую форму должно иметь обтекаемое тело? 19. В чем состоит эффект Магнуса? Задачи для самостоятельного решения: 1. Масса вертолета 3·103 кг, мощность мотора 325 кВт, диаметр винта, отбрасывающего вниз цилиндрическую струю воздуха того же диаметра, равен 8 м. За какое время вертолет поднимется на высоту 100 м? Принять плотность воздуха 1,3 кг/м3, движение равноускоренным. Сопротивлением воздуха пренебречь. 2. В бак равномерно поступает вода, скорость наполнения которого 3. Площадь поршня в шприце 4. В широкий сосуд, в нижней части которого имеется небольшое отверстие, налита вода до высоты 5. На гладком столе находится открытый цилиндрический сосуд высотой 6. На Рис.3.2.1 дана схема так называемой трубки Вентури, позволяющей определять ежесекундный расход жидкости (расходомер). Принцип действия трубки ясен из рисунка. Зная, чему рана площадь поперечного сечения б) мощность потока. 7. Найти скорость 8. В дне цилиндрического сосуда диаметром 9. на столе стоит сосуд с водой, в боковой поверхности которого имеется малое отверстие, расположенное на расстоянии 10. Цилиндрический бак высотой 11.
 течет жидкость. течет жидкость.  Разность уровней этой жидкости в трубах Разность уровней этой жидкости в трубах 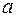 и и 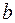 равна равна  10 см. (Рис.3.2.2) Диаметры трубок 10 см. (Рис.3.2.2) Диаметры трубок 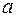 и и 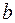 одинаковы. Найти скорость одинаковы. Найти скорость  течения жидкости в трубе течения жидкости в трубе  . .
12.
 Воздух продувается через трубку Воздух продувается через трубку  . За единицу времени через трубку . За единицу времени через трубку  протекает объем воздуха протекает объем воздуха  5 л/мин. (Рис.3.2.3) Площадь поперечного сечения широкой части трубки 5 л/мин. (Рис.3.2.3) Площадь поперечного сечения широкой части трубки  равна равна  2 см2, а узкой ее части и трубки 2 см2, а узкой ее части и трубки  равна равна  0,5 см2. Найти разность уровней 0,5 см2. Найти разность уровней  воды, налитой в трубку воды, налитой в трубку  . Плотность воздуха . Плотность воздуха  1,32 кг/м3. 1,32 кг/м3.
13. Стальной шарик диаметром 14. Вода течет по трубе, причем за единицу времени через поперечное сечение трубы протекает объем воды 15. Трубка Пито (Рис.3.2.4) установлена по оси газопровода, площадь внутреннего сечения которого равна 16. Изогнутую трубку опустили в поток воды. Скорость потока относительно трубки 17. Вертикальная струя идеальной жидкости вытекает из горизонтального отверстия радиуса 18.
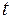 ? ?  Объем воды в цилиндре равен Объем воды в цилиндре равен  , площадь сечения отверстия , площадь сечения отверстия 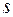 , причем , причем 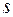 значительно меньше площади поршня. Трение и вязкость пренебрежимо малы. значительно меньше площади поршня. Трение и вязкость пренебрежимо малы.
19. Тонкостенный цилиндрический сосуд погрузили в идеальную жидкость до верхнего (открытого) основания. В нижнем, закрытом торце имеется малое отверстие. Известны высота сосуда 20. По трубе радиуса 21. Радиус сечения трубопровода монотонно уменьшается по закону 22. В чан равномерной струей наливается вода. Приток воды равен 150 см3/с. В дне чана имеется отверстие площадью 0,5 см2. Какого уровня может достигнуть вода в чане? 23. Цилиндрический сосуд высотой 70 см с площадью дна 600 см2 наполнен водой. В дне сосуда образовалось отверстие с площадью 1 см2. а) Как движется верхний уровень воды в сосуде? б) Сколько времени понадобится для полного опорожнения сосуда? в) Сколько времени понадобится для опорожнения сосуда наполовину? г) Увеличится или уменьшится время опорожнения сосуда, если сосуд будет совершать гармонические колебания в вертикальном направлении? 24. а) Показать, что в схеме на Рис.3.2.6 работа при перемещении правого поршня больше работы при перемещении левого поршня. б) За счет чего производится дополнительная работа при использовании схемы как механизма для увеличения силы?
 
25. Площадь поршня в спринцовке (Рис.3.2.7) 26. Какова максимальная скорость течения воды при температуре 150 по трубе с внутренним диаметром 2 см, при которой течение еще остается ламинарным? |
|
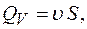
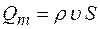 ,
,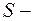 площадь поперечного сечения трубки тока,
площадь поперечного сечения трубки тока,  скорость жидкости,
скорость жидкости,  плотность жидкости.
плотность жидкости. ,
, и
и  площади поперечного сечения трубки тока в двух местах;
площади поперечного сечения трубки тока в двух местах;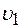 и
и  соответствующие скорости течений.
соответствующие скорости течений. const.
const.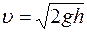 ,
, уровень жидкости относительно отверстия.
уровень жидкости относительно отверстия. ,
, сила поверхностного натяжения, действующая на контур
сила поверхностного натяжения, действующая на контур  , ограничивающий поверхность жидкости.
, ограничивающий поверхность жидкости.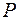 , создаваемое сферической поверхностью жидкости:
, создаваемое сферической поверхностью жидкости: ,
, радиус сферической поверхности.
радиус сферической поверхности. ,
, краевой угол;
краевой угол;  r – радиус капилляра.
r – радиус капилляра. ,
, расстояние между плоскостями.
расстояние между плоскостями. ,
,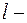 длина трубки;
длина трубки;  разность давлений на концах трубки;
разность давлений на концах трубки;  коэффициент внутреннего сопротивления.
коэффициент внутреннего сопротивления. ,
, средняя по сечению скорость течения жидкости;
средняя по сечению скорость течения жидкости;  ,
, , действующая со стороны потока жидкости на медленно движущийся в ней шарик (формула Стокса):
, действующая со стороны потока жидкости на медленно движущийся в ней шарик (формула Стокса): ,
,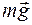 , направленная вниз, и сила Архимеда
, направленная вниз, и сила Архимеда  , направленная вверх. Так как льдина плавает, запишем условие равновесия:
, направленная вверх. Так как льдина плавает, запишем условие равновесия:
 (1)
(1)
 1030кг/м3
1030кг/м3
 900 кг/м3
900 кг/м3
 и объема подводной части
и объема подводной части  :
: (2)
(2) . (3)
. (3) . (4)
. (4) ,
, (5).
(5). ,
,  ,
,  ,
, 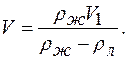
 1030·250/(1030-900) м3=1981 м3.
1030·250/(1030-900) м3=1981 м3. отверстия в дне сосуда, чтобы вода в нем держалась на постоянном уровне
отверстия в дне сосуда, чтобы вода в нем держалась на постоянном уровне 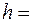 8,3 см?
8,3 см?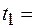 1 с
1 с
 ,
,
 . Площадь поперечного сечения отверстия:
. Площадь поперечного сечения отверстия:  .
. или
или  ,
, .
. .
. м=1,4·10-2м=1,4 см.
м=1,4·10-2м=1,4 см. 0,3 мм, если динамическая вязкость воздуха
0,3 мм, если динамическая вязкость воздуха  1,2·10-5 Па·с?
1,2·10-5 Па·с? . При увеличении скорости падения сила сопротивления растет. Максимальной скорости капля достигнет, когда сила тяжести и сила сопротивления воздуха будут равны:
. При увеличении скорости падения сила сопротивления растет. Максимальной скорости капля достигнет, когда сила тяжести и сила сопротивления воздуха будут равны: .
.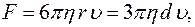
 .
.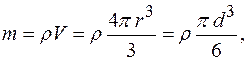
 ,
, .
.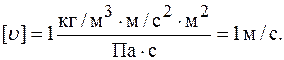
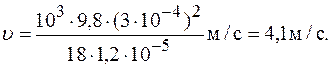
 . На дне бака имеется отверстие площадью
. На дне бака имеется отверстие площадью  . Какой высоты может достичь уровень воды в баке?
. Какой высоты может достичь уровень воды в баке? . Сколько времени будет вытекать жидкость из шприца, расположенного горизонтально, если на поршень давить силой
. Сколько времени будет вытекать жидкость из шприца, расположенного горизонтально, если на поршень давить силой  , а сверху нее – слой масла толщиной
, а сверху нее – слой масла толщиной  . Плотность воды
. Плотность воды  , масла -
, масла -  . а) С какой скоростью вода начнет вытекать из сосуда, если открыть отверстие? б) По какому закону будет изменяться уровень воды в сосуде в зависимости от времени, если площадь сечения отверстия в
. а) С какой скоростью вода начнет вытекать из сосуда, если открыть отверстие? б) По какому закону будет изменяться уровень воды в сосуде в зависимости от времени, если площадь сечения отверстия в 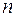 раз меньше площади сечения сосуда?
раз меньше площади сечения сосуда? , доверху наполненный водой. а) На какой высоте нужно сделать отверстие в стенке сосуда, чтобы струя жидкости падала на стол на максимальном расстоянии от боковой поверхности сосуда? Понижением уровня жидкости в сосуде пренебречь. б) Как будет меняться дальность полета струи с течением времени при понижении уровня воды? Площади сечения сосуда и отверстия равны
, доверху наполненный водой. а) На какой высоте нужно сделать отверстие в стенке сосуда, чтобы струя жидкости падала на стол на максимальном расстоянии от боковой поверхности сосуда? Понижением уровня жидкости в сосуде пренебречь. б) Как будет меняться дальность полета струи с течением времени при понижении уровня воды? Площади сечения сосуда и отверстия равны  , определите: а) сколько воды проходит через магистраль за время
, определите: а) сколько воды проходит через магистраль за время  30 мин через поперечное сечение трубы протекает масса газа
30 мин через поперечное сечение трубы протекает масса газа  0,51 кг. Плотность газа
0,51 кг. Плотность газа  2 см.
2 см. этого уровня. Найти значение этой скорости для высоты
этого уровня. Найти значение этой скорости для высоты  от дна сосуда и на расстоянии
от дна сосуда и на расстоянии  от уровня воды. Уровень воды в сосуде поддерживается постоянным. На каком расстоянии
от уровня воды. Уровень воды в сосуде поддерживается постоянным. На каком расстоянии  25 см,
25 см,  16 см; б)
16 см; б) 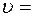 0,185 см/с в большом сосуде, наполненном касторовым маслом. Найти динамическую вязкость
0,185 см/с в большом сосуде, наполненном касторовым маслом. Найти динамическую вязкость  касторового масла.
касторового масла. трубы движение воды остается ламинарным, считая, что ламинарность движения воды в цилиндрической трубе сохраняется при числе Рейнольдса
трубы движение воды остается ламинарным, считая, что ламинарность движения воды в цилиндрической трубе сохраняется при числе Рейнольдса  3000?
3000? и
и  .
. 12 см. На какую высоту
12 см. На какую высоту  со скоростью
со скоростью 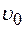 . Найти радиус струи на расстоянии
. Найти радиус струи на расстоянии  1. Найти время, за которое наполнится сосуд.
1. Найти время, за которое наполнится сосуд. течет стационарный поток вязкой жидкости. На оси трубы ее скорость равна
течет стационарный поток вязкой жидкости. На оси трубы ее скорость равна  от оси трубы.
от оси трубы. , где
, где  0,5 м-1,
0,5 м-1, 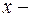 расстояние от начала трубопровода. Найти отношение чисел Рейнольдса в сечениях, отстоящих друг от друга на
расстояние от начала трубопровода. Найти отношение чисел Рейнольдса в сечениях, отстоящих друг от друга на  3,2 м.
3,2 м. 0,5 кг и если ход поршня
0,5 кг и если ход поршня 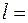 4см?
4см?