|
|
Занятие 3. Механические колебания и волны. Маятники.Краткие теоретические основы и формулы Уравнение плоской волны
где Разность фаз колебаний точек среды, отстоящих друг от друга на расстоянии
Дифференциальное уравнение колебаний материальной точки и его решение:
где Разность фаз колебаний двух точек среды, расстояние между которыми (разность хода) равно
Условие максимумов Амплитуда колебаний среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн (при условии, что фазы колебаний обоих источников совпадают):
где Условие минимумов Амплитуда колебаний среды в данной точке минимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна нечетному числу полуволн:
Эффект Доплера для звуковых волн
где Период колебаний пружинного маятника
где Период колебаний математического маятника
где Период колебаний физического маятника
где Период крутильных колебаний тела, подвешенного на упругой нити:
где Полная энергия гармонических колебаний
Дифференциальное уравнение затухающих колебаний и его решение:
где
Логарифмический декремент затухания
где Уравнение вынужденных колебаний и его установившееся решение:
Максимум амплитуды смещения достигается при: Вопросы для ответа у доски: 1. Движение под действием упругих и квазиупругих сил. Пружинный маятник. Выясните условия, при которых возникает колебательное движение. Дайте классификацию сил, действующих на колеблющуюся систему. Получите дифференциальное уравнение колебания пружинного маятника и решите его. Математический, физический и крутильный маятники. Энергия колеблющегося тела. Получите дифференциальные уравнения колебаний математического, физического и крутильного маятников и покажите, что колебания всех рассмотренных маятников можно описывать одним дифференциальным уравнением. Запишите решение уравнения для перечисленных колебаний. Найдите кинетическую, потенциальную и полную энергию маятников. Затухающие колебания. Составьте и решите дифференциальное уравнение для системы, совершающей затухающие колебания под действием силы трения, пропорциональной скорости системы. Укажите важнейшие характеристики затухающих колебаний и их связь с параметрами колеблющейся системы. Вынужденные колебания. Составьте и решите дифференциальное уравнение для системы, совершающей вынужденные колебания под действием силы, меняющейся по гармоническому закону. Покажите, что установившиеся вынужденные колебания происходят с частотой вынуждающей силы, а их амплитуда зависит от соотношения собственной и вынужденной частоты. Постройте соответствующий график. Примеры решения задач: Задача 1. На каком расстоянии друг от друга находятся две соседние точки, колеблющиеся в противофазе, если длина волны 16 м.
Отсюда расстояние, на котором находятся две соседние точки:
Подставим числовые данные, получим:
Ответ: 8 м. Задача 2. Найти положение узлов и пучностей и начертить график стоячей волны, если: а) отражение происходит от менее плотной среды; б) отражение происходит от более плотной среды. Длина бегущей волны Решение:
 Стоячей называется волна, которая образуется в результате наложения двух бегущих синусоидальных когерентных волн, распространяющихся навстречу друг другу. В отличие от бегущей волны она состоит из узлов и пучностей, причем расстояние между двумя соседними узлами или пучностями есть величина постоянная, называемая длиной стоячей волны, Стоячей называется волна, которая образуется в результате наложения двух бегущих синусоидальных когерентных волн, распространяющихся навстречу друг другу. В отличие от бегущей волны она состоит из узлов и пучностей, причем расстояние между двумя соседними узлами или пучностями есть величина постоянная, называемая длиной стоячей волны,
где
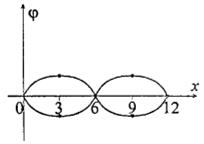 а) Если отражение происходит от менее плотной среды, то положение узлов будет определяться из условия а) Если отражение происходит от менее плотной среды, то положение узлов будет определяться из условия  (1), где (1), где 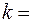 0, 1, 2, … Подставляя в (2) значения 0, 1, 2, … Подставляя в (2) значения  и и 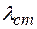 , получаем , получаем 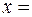 3, 9, 15см, …. Положение пучностей будет определяться из условия 3, 9, 15см, …. Положение пучностей будет определяться из условия  (3). Подставляя в (3) значения (3). Подставляя в (3) значения  и и 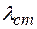 , получаем , получаем 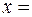 0, 6, 12, 18см, …. 0, 6, 12, 18см, ….
 б) Если отражение происходит от более плотной среды, то узлы и пучности поменяются местами и положение узлов будет определяться из условия (3), т.е. б) Если отражение происходит от более плотной среды, то узлы и пучности поменяются местами и положение узлов будет определяться из условия (3), т.е. 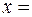 0, 6, 12, 18см, …, а положение пучностей – из условия (2), т.е. 0, 6, 12, 18см, …, а положение пучностей – из условия (2), т.е. 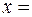 3, 9, 15см, …. 3, 9, 15см, ….
Задача 3. Найти закон изменения периода колебания математического маятника с поднятием маятника над поверхностью Земли. Решение: Период колебаний математического маятника определяется формулой:
Период колебаний физического маятника
где Период Сила, с которой тело массой
где Из уравнения (3) находим ускорение свободного падения:
Подставляя выражение (4) в (1), находим закон изменения периода колебания маятника:
Следовательно, период колебаний маятника прямо пропорционален расстоянию от маятника до центра Земли. Ответ: Задача 4. Как изменится период вертикальных колебаний груза, висящего на двух пружинах, если от последовательного соединения пружин перейти к параллельному их соединению? Решение: Сила упругости пружины по закону Гука
С другой стороны, При параллельном соединении пружин общая жесткость системы
Отношение периодов колебаний:
Период колебаний уменьшится в 2 раза. Ответ: период колебаний груза уменьшится в 2 раза. Задача 5. Найти логарифмический декремент затухания Решение: По формулам для затухающих колебаний:
Период колебаний математического маятника: Подставляя (2) в уравнение (1), получим:
По условию
Прологарифмируем уравнение (4):
Отсюда логарифмический декремент затухания:
Подставив числовые данные, находим логарифмический декремент затухания колебаний математического маятника:
Ответ: Вопросы и задания для самопроверки 1. Роль начальных условий при гармонических колебаниях. 2. Примеры колебаний под действием упругих сил. 3. Примеры колебаний под действием квазиупругих сил. Чем определяется коэффициент квазиупругой возвращающей силы? 4. Какие колебания называются собственными; свободными? Чем определяется частота собственных колебаний? 5. На пружине с коэффициентом упругости k колеблется гиря массой m. Как изменится период колебаний, если гирю заменить другой, большей массы; если при прежней гире укоротить пружину? 6. Почему период математического маятника не зависит от массы, а период физического маятника зависит от его момента инерции? Когда на практике используют математический маятник для измерения ускорения свободного падения? Какую выгоднее брать массу – малую или большую? Почему? 7. Можно ли формулу для периода колебаний физического маятника использовать для измерений момента инерции тела? 8. От каких величин зависит полная энергия тела, совершающего прямолинейные гармонические колебания? 9. Чем определяется затухание колебаний? 10. Какой смысл имеет понятие периода затухающих колебаний, хотя они непериодические? 11. Что такое декремент и логарифмический декремент затухающих колебаний? 12. Какие важные особенности затухания колебаний характеризуются декрементом затухания? 13. Что называется добротностью колебательной системы? 14. Изменится ли период колебаний маятника, если мы его поместим в воду (маятнику придана обтекаемая форма и можно принять, что трение о воду равно нулю)? 15. Какую частоту называют резонансной? Будет ли она одинакова для одной и той же колеблющейся системы при различных коэффициентах затухания? 16. Какое свойство резонансной кривой характеризует добротность? Задачи для самостоятельного решения: 1. Шарик массой 0,01кг совершает гармонические колебания с амплитудой 0,03м и частотой 10с-1. Начальная фаза колебаний равна нулю. Получите закон изменения силы, действующей на шарик. Определите: а) полную энергию шарика; б) значение действующей силы и отношение потенциальной энергии к кинетической для момента времени, когда шарик удален от положения равновесия на 0,02м. 2. Точка совершает колебания, описываемые уравнением 3. Автомобиль массой 1500кг при движении по ребристой дороге совершает гармонические колебания в вертикальном направлении с периодом 0,5с и с амплитудой 0,15м. Определите максимальную силу давления, действующую на каждую из четырех рессор автомобиля. 4. Математический маятник совершает колебания с амплитудой 5. Амплитуда затухающих колебаний математического маятника за время 6. После 10 полных колебаний точки ее амплитуда колебаний уменьшается от 10 до 6 см. Коэффициент затухания равен 0,2. Получите закон движения точки. 7. Найти отношение кинетической энергии 8. Амплитуда гармонических колебаний материальной точки 9. К пружине подвешен груз. Максимальная кинетическая энергия 10. К резиновому шнуру длиной 11. Ареометр массой 12. Период затухающих колебаний 13. Логарифмический декремент затухания математического маятника 14. Математический маятник длиной 15. Тело массой 16. Концы недеформированной пружины жесткостью 17.
 в системе (Рис.3.3.2), в системе (Рис.3.3.2), 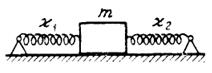 если жесткости пружинок равны если жесткости пружинок равны  и и 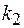 , а трение пренебрежимо мало. В положении равновесия можно считать, что пружинки не деформированы. , а трение пренебрежимо мало. В положении равновесия можно считать, что пружинки не деформированы.
18.
 Однородный стержень положили на два быстро вращающихся блока, как показано на Рис.3.3.3. Расстояние между осями блоков Однородный стержень положили на два быстро вращающихся блока, как показано на Рис.3.3.3. Расстояние между осями блоков 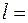 20 см, коэффициент трения между стрежнем и блоками 20 см, коэффициент трения между стрежнем и блоками 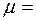 0,18. Показать, что стержень будет совершать гармонические колебания. Найти их период. 0,18. Показать, что стержень будет совершать гармонические колебания. Найти их период.
19. Представим себе шахту, пронизывающую Землю по ее оси вращения. Считая Землю за однородный шар и пренебрегая сопротивлением воздуха, найти: а) уравнение движения тела, упавшего в шахту; б) время, которое понадобится этому телу, чтобы достичь противоположного конца шахты; в) скорость тела в центре Земли. 20. К нерастянутой пружине, верхний конец которой закреплен, подвесили и без толчка отпустили тело массы 21. Математический маятник совершает колебания в среде, для которой логарифмический декремент затухания 22. К невесомой пружине подвесили грузик, и она растянулась на |
|

 волновое число,
волновое число,  модуль скорости распространения волны,
модуль скорости распространения волны,  длина волны,
длина волны, 


 0,
0, 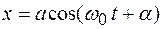 ,
,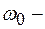 собственная частота колебаний.
собственная частота колебаний.
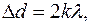
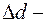 разность хода двух волн;
разность хода двух волн; 

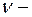 частота звуковых колебаний, воспринимаемая движущимся приемником;
частота звуковых колебаний, воспринимаемая движущимся приемником;  частота звуковых колебаний, испускаемых источником;
частота звуковых колебаний, испускаемых источником; 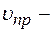 скорость прибора относительно среды;
скорость прибора относительно среды;  скорость источника звука относительно среды.
скорость источника звука относительно среды.
 масса груза,
масса груза,  коэффициент упругости пружины.
коэффициент упругости пружины.
 ускорение свободного падения,
ускорение свободного падения, 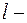 длина нити маятника.
длина нити маятника.
 приведенная длина физического маятника,
приведенная длина физического маятника,  момент инерции,
момент инерции, 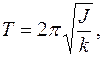

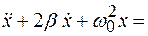 0,
0,  ,
, коэффициент затухания;
коэффициент затухания;  частота затухающих колебаний;
частота затухающих колебаний;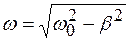 .
. и добротность
и добротность  :
: ,
, период затухающих колебаний.
период затухающих колебаний. , где:
, где:
 .
.
 и
и 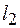 от источника колебаний, имеют разность фаз:
от источника колебаний, имеют разность фаз:

 16 м
16 м




 8 м.
8 м. (1),
(1), в (1), получим
в (1), получим  6см.
6см. . (1)
. (1)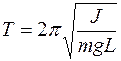 , (2)
, (2)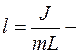 приведенная длина маятника.
приведенная длина маятника.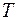 зависит от ускорения свободного падения.
зависит от ускорения свободного падения. (3)
(3)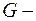 гравитационная постоянная,
гравитационная постоянная,  масса Земли,
масса Земли,  расстояние от центра Земли до тела.
расстояние от центра Земли до тела.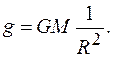 (4)
(4) . (5)
. (5)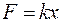 . Если к пружине подвесить груз массой
. Если к пружине подвесить груз массой  , отсюда удлинение пружины
, отсюда удлинение пружины  . Если две пружины соединить последовательно, то их удлинения будут равны, а общее удлинение составит:
. Если две пружины соединить последовательно, то их удлинения будут равны, а общее удлинение составит: (1).
(1). (2), отсюда, приравняв правые части уравнений (1) и (2), получаем:
(2), отсюда, приравняв правые части уравнений (1) и (2), получаем: 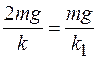 или
или  .
. . Таким образом, периоды колебаний при последовательном и параллельном соединении пружин соответственно равны:
. Таким образом, периоды колебаний при последовательном и параллельном соединении пружин соответственно равны: и
и  ,
, .
. 1 мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника
1 мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника  , отсюда
, отсюда  (1).
(1). (2).
(2). (3).
(3). , тогда из уравнения (3) получим:
, тогда из уравнения (3) получим: (4).
(4). ,
, .
.

 (м). В некоторый момент времени сила, действующая на точку, и ее потенциальная энергия равны 5·10-3 Н и 10-4 Дж. Чему равна фаза колебаний и кинетическая энергия точки в этот момент времени?
(м). В некоторый момент времени сила, действующая на точку, и ее потенциальная энергия равны 5·10-3 Н и 10-4 Дж. Чему равна фаза колебаний и кинетическая энергия точки в этот момент времени?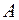 . Спустя время
. Спустя время 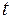 после начала движения из положения равновесия смещение маятника оказалось равным
после начала движения из положения равновесия смещение маятника оказалось равным  уменьшается в
уменьшается в  . а) Чему равен логарифмический декремент затухания
. а) Чему равен логарифмический декремент затухания  , отсчитываемое после начала наблюдений, амплитуда уменьшится еще в
, отсчитываемое после начала наблюдений, амплитуда уменьшится еще в 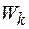 , к ее потенциальной энергии
, к ее потенциальной энергии  для моментов, когда смещение точки от положения равновесия составляет: а)
для моментов, когда смещение точки от положения равновесия составляет: а)  /4; б)
/4; б) 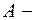 амплитуда колебаний.
амплитуда колебаний.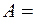 2 см, полная энергия колебаний
2 см, полная энергия колебаний 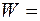 0,3 мкДж. При каком смещении
0,3 мкДж. При каком смещении 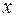 от положения равновесия на колеблющуюся точку действует сила
от положения равновесия на колеблющуюся точку действует сила  22мкН?
22мкН? 1 Дж. Амплитуда колебаний
1 Дж. Амплитуда колебаний 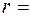 1 мм подвешена гиря массой
1 мм подвешена гиря массой  0,5 кг. Зная, что модуль Юнга резины
0,5 кг. Зная, что модуль Юнга резины  3МН/м2, найти период
3МН/м2, найти период  соотношением
соотношением 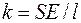 , где
, где 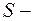 площадь поперечного сечения резины,
площадь поперечного сечения резины,  3,4с. Считая колебания незатухающими, найти плотность жидкости
3,4с. Считая колебания незатухающими, найти плотность жидкости  , в которой плавает ареометр. Диаметр вертикальной цилиндрической трубки ареометра
, в которой плавает ареометр. Диаметр вертикальной цилиндрической трубки ареометра  1 см.
1 см. 1,6; начальная фаза
1,6; начальная фаза 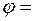 0. При
0. При  /4 смещение точки
/4 смещение точки  7 см, начальной фазой
7 см, начальной фазой  , под действием которой установились вынужденные колебания. Уравнение вынужденных колебаний имеет вид
, под действием которой установились вынужденные колебания. Уравнение вынужденных колебаний имеет вид  см. Найти (с числовыми коэффициентами) уравнение собственных колебаний и уравнение внешней периодической силы.
см. Найти (с числовыми коэффициентами) уравнение собственных колебаний и уравнение внешней периодической силы. , где
, где  его смещение из начального положения; б) максимальное и минимальное натяжения пружины.
его смещение из начального положения; б) максимальное и минимальное натяжения пружины.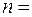 2 раза? Во сколько раз следует увеличить сопротивление среды, чтобы колебания стали невозможны?
2 раза? Во сколько раз следует увеличить сопротивление среды, чтобы колебания стали невозможны? 9,8см. С каким периодом будет колебаться грузик, если ему дать небольшой толчок в вертикальном направлении? Логарифмический декремент затухания
9,8см. С каким периодом будет колебаться грузик, если ему дать небольшой толчок в вертикальном направлении? Логарифмический декремент затухания