|
|
Занятие 3. Кинематика вращательного движения материальной точки.Краткие теоретические сведения Основные формулы Положение твердого тела (при заданной оси вращения) задается углом поворота Кинематическое уравнение вращательного движения
Мгновенная угловая скорость
Угловое ускорение
Связь линейных характеристик с угловыми характеристиками
Уравнение равномерного вращения
Уравнение равнопеременного вращения
Частота вращения (число оборотов в единицу времени)
Период (время одного полного оборота)
Циклическая (круговая) частота
Вопросы для ответа у доски: 1. Описание вращательного движения материальной точки. Угловая скорость, угловое ускорение и их связь с соответствующими линейными величинами. Введите среднюю и мгновенную угловые скорости и ускорение. Определите период и частоту равномерного движения. Установите связь между угловыми и линейными величинами скорости и ускорения. Введите единицы указанных величин и дайте их определение. Приведите пример задания вращательного движения и найдите угловую скорость, угловое ускорение и соответствующие линейные величины. 2. Угловая скорость как векторная величина. Связь между векторами линейной и угловой скоростей. Покажите, что поворот на малый угол можно сопоставить с вектором углового перемещения. Введите вектор угловой скорости, определив его направление и величину. Получите формулу Эйлера, устанавливающую связь между векторами линейной и угловой скоростей. 3. Угловое ускорение как вектор. Ускорение точки при вращательном движении. Введите вектор углового ускорения. Определите его направление для ускоренного и замедленного движения. Получите выражение для полного линейного ускорения через угловые величины. Выясните физический смысл каждого слагаемого вектора ускорения изобразите на рисунке расположение векторов, определяющих центростремительное и тангенциальное ускорения для ускоренного и замедленного движения. 4. Сопоставление линейных и угловых характеристик вращательного движения точки. Равномерное и равнопеременное вращение материальной точки и формулы, описывающие это движение. Покажите, как, не производя вычислений, можно путем замены линейных величин соответствующими угловыми величинами получить различные формулы, описывающие равномерное и равнопеременное движение. Примеры решения задач: Задача 1. Период вращения одного колеса вдвое меньше периода другого колеса, а его радиус втрое больше радиуса другого колеса. Сравнить нормальные ускорения для точек обода обоих колес.
Для точек обода первого колеса:
для точек обода второго колеса:
Отношение нормальных ускорений точек обода первого и второго колес:
Ответ: Задача 2. Найти радиус Решение: Вектор
для первой точки, лежащей на ободе колеса: для второй точки, лежащей ближе к оси колеса:
Отсюда
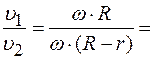 2,5; 2,5;  2,5; 2,5;
Подставив числовые значения, находим радиус вращающегося колеса: 1,5· Ответ: Задача 3. Точка движется по окружности радиусом Решение: Нормальное ускорение:
При равноускоренном движении среднее число оборотов в единицу времени:
где
Частота оборотов: Угловое ускорение
Из уравнения (1) находим
подставив числовые данные получим:
Ответ: Вопросы для самопроверки: 1. Как описывается вращательное движение материальной точки? 2. Что называется угловой скоростью вращательного движения? Дайте определение единицы измерения угловой скорости. Какая единица измерения угловой скорости часто используется в технике? 3. Что такое период и частота вращательного движения? Какая существует связь между ними? 4. Дайте определение углового ускорения и единицы его измерения. 5. Какая линейная величина аналогична угловому ускорению и как они связаны между собой? 6. Как записывается закон равномерного и равнопеременного движения точки через угловые величины? 7. Как определяется направление вектора угловой скорости? Чем отличается этот вектор отранее рассмотренных векторов? Задачи для самостоятельного решения: 1. Барабан начинает вращаться с постоянным угловым ускорением 2. Перед наблюдателем в вертикальной плоскости вращается диск, разделенный на 3. В некоторый момент времени вращение одного диска описывается уравнением 4. Автомобиль движется по прямому шоссе так, что его движение описывается уравнением 5. Зубчатое колесо радиусом 6. Найти угловую скорость 7. Колесо, вращаясь равноускоренно, через время 8. Колесо радиусом 9. Колесо вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением 10. Точка движется, замедляясь, по окружности радиуса 11. 12.
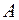 движется по окружности радиуса движется по окружности радиуса 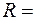 50 см так, что ее радиус-вектор 50 см так, что ее радиус-вектор 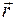 относительно точки относительно точки  . (Рис.1.3.2) поворачивается с постоянной скоростью . (Рис.1.3.2) поворачивается с постоянной скоростью  0,4 рад/с. Найти модуль скорости частицы, а также модуль и направление ее полного ускорения. 0,4 рад/с. Найти модуль скорости частицы, а также модуль и направление ее полного ускорения.
13. Колесо вращается вокруг неподвижной оси так, что угол поворота зависит от времени как 14. Снаряд вылетел со скоростью 15. Твердое тело вращается вокруг неподвижной оси по закону 16. Точка 17. Поезд движется по закруглению с радиусом 400м, причем его ускорение (тангенциальное) равно 0,2 м/с2. Определить его нормальное и полное ускорение в тот момент, когда его скорость равна 10 м/с. 18.
 Три самолета выполняют разворот, двигаясь на расстоянии 60 м друг от друга (Рис.1.3.3). Средний самолет летит со скоростью 360 км/ч, двигаясь по дуге окружности радиусом 600 м. Определить ускорение каждого самолета. Три самолета выполняют разворот, двигаясь на расстоянии 60 м друг от друга (Рис.1.3.3). Средний самолет летит со скоростью 360 км/ч, двигаясь по дуге окружности радиусом 600 м. Определить ускорение каждого самолета.
19. Колесо, вращающееся с частотой оборотов 1500 мин-1, при торможении стало вращаться равномерно замедленно и остановилось через 30 с. Найти угловое ускорение и число оборотов с момента начала торможения до остановки. 20. 21.
|
|
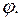
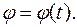
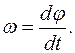
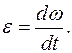

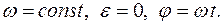
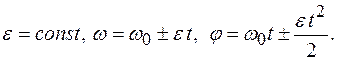
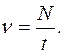
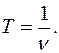

 где
где  число оборотов.
число оборотов.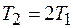
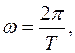 где
где  период вращения.
Нормальное ускорение при вращательном движении:
период вращения.
Нормальное ускорение при вращательном движении:


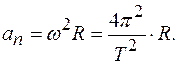
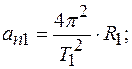
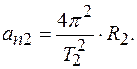
 12.
12.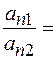 12.
12. вращающегося колеса, если известно, что линейная скорость
вращающегося колеса, если известно, что линейная скорость 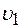 точки, лежащей на ободе, в 2,5 раза больше линейной скорости
точки, лежащей на ободе, в 2,5 раза больше линейной скорости 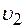 точки, лежащей на расстоянии
точки, лежащей на расстоянии 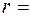 5 см ближе к оси колеса.
5 см ближе к оси колеса.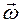 перпендикулярен плоскости Рис.1.3.1, следовательно, в скалярном виде:
перпендикулярен плоскости Рис.1.3.1, следовательно, в скалярном виде: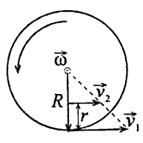
 ,
,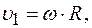
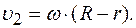
 Найти нормальное ускорение
Найти нормальное ускорение 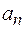 точки через время
точки через время  20 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки
20 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки 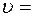 10 см/с.
10 см/с. где
где  , отсюда
, отсюда  (1)
(1)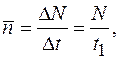
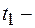 момент времени, соответствующий концу пятого оборота,
момент времени, соответствующий концу пятого оборота,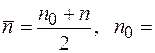 0, значит,
0, значит,  ,
, 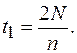
 ,
, 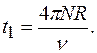
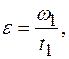 где
где 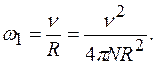
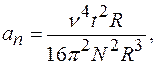
 м/с2 =0,01 м/с2.
м/с2 =0,01 м/с2.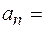 0,01 м/с2.
0,01 м/с2.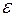 вокруг своей оси. По какому закону меняется с течением времени угол
вокруг своей оси. По какому закону меняется с течением времени угол  между векторами скорости и полного ускорения произвольной точки барабана?
между векторами скорости и полного ускорения произвольной точки барабана?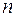 одинаковых секторов. Около диска закреплен неподвижный указатель. Наблюдая за вращением диска, установили, что дуга первого сектора прошла мимо указателя за
одинаковых секторов. Около диска закреплен неподвижный указатель. Наблюдая за вращением диска, установили, что дуга первого сектора прошла мимо указателя за 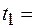 4 с, дуга соседнего – за
4 с, дуга соседнего – за 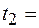 5 с. После этого диск повернулся на угол
5 с. После этого диск повернулся на угол 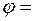 0,75
0,75 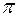 и остановился. Считая движение диска равнозамедленным, определите его угловое ускорение.
и остановился. Считая движение диска равнозамедленным, определите его угловое ускорение.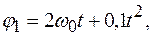 второго -
второго -  Через время
Через время 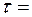 5с первый диск опережает второй на пять оборотов. На сколько оборотов первый диск будет опережать второй к тому моменту, когда второй диск остановится?
5с первый диск опережает второй на пять оборотов. На сколько оборотов первый диск будет опережать второй к тому моменту, когда второй диск остановится?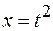 (
( 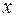 в метрах). Радиус колеса автомобиля
в метрах). Радиус колеса автомобиля 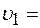 1+3
1+3 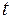 и
и 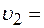 1-
1- 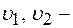 в м/с). а) Составьте уравнения движения, скорости и ускорения оси колеса. Определите: б) скорости и ускорения точек обода, лежащих на концах горизонтального диаметра, к концу второй секунды движения; в) ускорения точек колеса, соприкасающихся с рейками. Решите задачу при условии, что рейки движутся в разные стороны.
в м/с). а) Составьте уравнения движения, скорости и ускорения оси колеса. Определите: б) скорости и ускорения точек обода, лежащих на концах горизонтального диаметра, к концу второй секунды движения; в) ускорения точек колеса, соприкасающихся с рейками. Решите задачу при условии, что рейки движутся в разные стороны.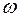 : а) суточного вращения Земли; б) часовой стрелки на часах; в) минутной стрелки на часах; г) искусственного спутника Земли, движущегося по круговой орбите с периодом вращения
: а) суточного вращения Земли; б) часовой стрелки на часах; в) минутной стрелки на часах; г) искусственного спутника Земли, движущегося по круговой орбите с периодом вращения  88 мин. Какова линейная скорость
88 мин. Какова линейная скорость  движения этого искусственного спутника, если известно, что его орбита расположена на расстоянии
движения этого искусственного спутника, если известно, что его орбита расположена на расстоянии 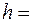 200 км от поверхности Земли.
200 км от поверхности Земли.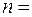 720 об/мин. Найти угловое ускорение
720 об/мин. Найти угловое ускорение 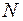 колеса за это время.
колеса за это время.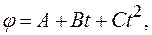 где
где 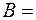 2 рад/с и
2 рад/с и 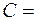 1 рад/с2. Для точек, лежащих на ободе колеса, найти через время
1 рад/с2. Для точек, лежащих на ободе колеса, найти через время 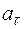 и нормальное
и нормальное 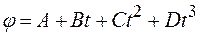 , где
, где  1 рад/с3. Найти радиус
1 рад/с3. Найти радиус 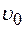 . Найти зависимость: а) скорости точки от времени и пройденного пути
. Найти зависимость: а) скорости точки от времени и пройденного пути 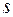 ; б) полного ускорения точки от
; б) полного ускорения точки от  Точка движется по дуге окружности радиуса
Точка движется по дуге окружности радиуса 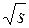 , где
, где  пройденный путь. Найти угол между векторами скорости и полного ускорения как функцию
пройденный путь. Найти угол между векторами скорости и полного ускорения как функцию 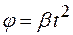 , где
, где 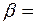 0,2 рад/с2 . Найти полное ускорение
0,2 рад/с2 . Найти полное ускорение 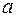 точки
точки 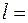 2,0 м. Считая движение снаряда в стволе равноускоренным, найти его угловую скорость вращения вокруг оси в момент вылета.
2,0 м. Считая движение снаряда в стволе равноускоренным, найти его угловую скорость вращения вокруг оси в момент вылета.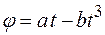 , где
, где  6,0 рад/с,
6,0 рад/с, 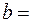 2 рад/с3. Найти средние значения угловой скорости и углового ускорения за промежуток времени от
2 рад/с3. Найти средние значения угловой скорости и углового ускорения за промежуток времени от  проходимый точкой
проходимый точкой 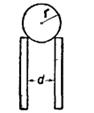 Некоторое тело начинает вращаться с постоянным угловым ускорением 0,04 с-2. Через сколько времени после начала вращения полное ускорение какой-либо точки тела будет направлено под углом 760 к направлению скорости этой точки?
Некоторое тело начинает вращаться с постоянным угловым ускорением 0,04 с-2. Через сколько времени после начала вращения полное ускорение какой-либо точки тела будет направлено под углом 760 к направлению скорости этой точки?