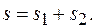Закон сохранения импульса выполняется для любого удара. Вопросы для ответа у доски:
1. Абсолютно неупругий удар.
Получите выражение для скорости двух не упруго столкнувшихся шаров. Найдите работу внутренних неконсервативных сил при деформации шаров и кинетическую энергию шаров после их соударения. Расскажите о практическом применении неупругого удара.
2. Абсолютно упругий удар.
Рассмотрите центральный удар двух упругих шаров и получите выражение скорости в векторной форме. Примените полученные формулы к различным частным случаям соударения двух шаров и шара с упругой стенкой.
Примеры решения задач:
Задача 1. Мяч массой 50гсвободно падает без начальной скорости с высоты 2м на пол и подскакивает на высоту 1м. Определить среднюю силу удара мяча о пол. Продолжительность удара 0,02с.
 Дано:
m=50г=
h1=2м
h2=1м
Δt=0,02с Дано:
m=50г=
h1=2м
h2=1м
Δt=0,02с
| СИ
0,05кг
| Решение:
Рис.2.5.1а Рис.2.5.1б
| Найти: 
|
|
| |
Поскольку высота подъёма мяча после удара изменилась, то это не абсолютно упругое соударение (  ). На рисунке (б) изображены силы: действующие на мяч при ударе - ). На рисунке (б) изображены силы: действующие на мяч при ударе - 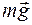 (сила тяжести) и (сила тяжести) и  (сила реакции опоры), а также сила (сила реакции опоры), а также сила  , действующая на пол со стороны мяча (сила удара мяча о пол – искомая сила). , действующая на пол со стороны мяча (сила удара мяча о пол – искомая сила).
По III закону Ньютона силы  и и  равны: равны: 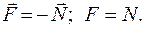
Найдём  и и  через II закон Ньютона, записанный в импульсной форме: через II закон Ньютона, записанный в импульсной форме:
 , ,
 – равнодействующая всех сил, действующих на мяч: – равнодействующая всех сил, действующих на мяч:
 . .
Тогда,
 , ,
где  и и  начальная и конечная скорости по отношению к удару, а не ко всему движению, то есть начальная и конечная скорости по отношению к удару, а не ко всему движению, то есть  скорость буквально перед ударом, скорость буквально перед ударом,  скорость сразу после удара, смотри рис. (а). скорость сразу после удара, смотри рис. (а).
Спроецируем уравнение на ось Y:
 . .
Отсюда:
 , ,
 скорости скорости  и и  найдём, пользуясь формулами кинематики: найдём, пользуясь формулами кинематики:
 ; ; 
 ; ; 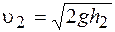
Тогда,
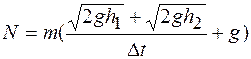
Вычислим:
 . .
В задаче необходимо определить среднююсилу удара мяча о пол. Во II законе Ньютона под  понимается постоянная, не меняющаяся с течением времени, сила, или, если сила меняется, то под понимается постоянная, не меняющаяся с течением времени, сила, или, если сила меняется, то под  понимается среднее значение силы. понимается среднее значение силы.
Так как в данной задаче сила удара  (а значит и (а значит и  ) меняется (от 0 до максимального значения и обратно до 0), то найденное значение силы удара и есть среднее значение этой силы. ) меняется (от 0 до максимального значения и обратно до 0), то найденное значение силы удара и есть среднее значение этой силы.
Итак,
 27,5Н. 27,5Н.
Ответ:  27,5Н. 27,5Н.
Задача 2. Снаряд массой 50кг, летящий параллельно рельсам со скоростью 400м/с, попадает в движущуюся платформу с песком массой 20т и застревает в песке. С какой скоростью будет двигаться платформа со снарядом, если:
1) она катилась навстречу снаряду со скоростью 2м/с;
2) она катилась в сторону движения снаряда со скоростью 2м/с;
3) она покоилась?
| Дано:
m1=50кг
υ1=400м/с
m2=20 т=
υ2=2м/с
| СИ
 кг кг
| Решение:
Рассмотрим систему: платформа с песком + снаряд.
Система не замкнута, так как на снаряд действует некомпенсированная (неуравновешенная другими силами) сила тяжести. Но, очевидно, что есть направление Х, вдоль которого не дей-
| Найти: 
| ствует сила 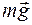 , (т.е. её проекция на ось Х равна 0). Для этого направления - вдоль оси Х - и будет выполняться закон сохранения импульса. , (т.е. её проекция на ось Х равна 0). Для этого направления - вдоль оси Х - и будет выполняться закон сохранения импульса.
В задаче можно выделить 2 состояния системы: до и после попадания снаряда в песок. На Рис.2.5.2 показаны импульсы тел системы в указанных состояниях.
 1) Случай 1: 1) Случай 1:
Взаимодействие тел – неупругое, так как после попадания снаряда в песок, система тел будет двигаться с общей скоростью  . .
Запишем закон сохранения импульса в проекции на ось Х:
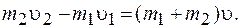
Выразим из полученного уравнения скорость  : :
 . .
Подставляя в выражение для u заданные числовые значения, получим:
 . .
2) Случай 2:

В данном случае закон сохранения импульса в проекции на ось Х будет выглядеть так:

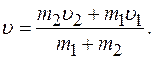
Вычисляя, получим: 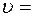 3 м/с. 3 м/с.
3) Случай 3:
 и выражение для и выражение для  примет вид: примет вид:  1м/с. 1м/с.
Ответ: 1) 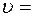 1м/с; 2) 1м/с; 2) 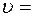 3 м/с;3) 3 м/с;3) 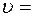 1м/с. 1м/с.
Задача 3. Баба копра масой 500 кг падает на сваю массой 120 кг со скоростью 4 м/с. Определить КПД удара бабы копра о сваю. Удар неупругий.
| Дано:
| Решение:
|  500 кг 500 кг
| Систему, состоящую из бабы копра и сваи, считаем замкнутой во время удара, когда силы ударного взаимодействия значительно превышают равнодействующую сил тяжести и силы реакции опоры. К такой системе можно применить закон сохранения импульса.
|  120 кг 120 кг
| 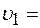 4 м/с 4 м/с
| 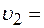 0 0
| Найти: 
| Решение:
Во время удара изменяется только кинетическая энергия тел, поэтому энергия  , затраченная на деформацию, равна разности значений механической энергии системы до и после удара: , затраченная на деформацию, равна разности значений механической энергии системы до и после удара:
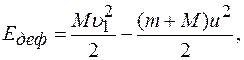 (1) (1)
где  общая скорость тел, входящих в систему, после неупругого удара. общая скорость тел, входящих в систему, после неупругого удара.
Из закона сохранения импульса:
 , ,
отсюда:
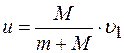 . (2) . (2)
Подставив в (1) значение скорости 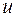 из (2), находим энергию деформации: из (2), находим энергию деформации:
 .(3) .(3)
Полезная энергия – это энергия, затраченная на деформацию. КПД удара:
 (4) (4)
Подставив числовые значения в (4), получаем:
 0,19. 0,19.
Ответ:  0,19. 0,19.
Вопросы и задания для самопроверки:
1. Что называется ударом?
2. Дайте определение прямого, центрального и косого ударов.
3. Какой удар называется абсолютно упругим; абсолютно неупругим?
4. Опишите процесс абсолютно упругого соударения двух тел. На какие два этапа делится процесс соударения? Как изменяется кинетическая и потенциальная энергия тел в процессе соударения?
5. Опишите процесс неупругого соударения тел.
6. Какими законами сохранения можно пользоваться при рассмотрении упругого и неупругого ударов?
Задачи для самостоятельного решения:
1. На стоящий на горизонтальном полу клин массой 5кг с высоты 1,5м падает шар массой 1кг и отскакивает в горизонтальном направлении. Найти горизонтальную скорость клина после удара. Трением пренебречь, удар шара о клин считать абсолютно упругим.
2. Какова средняя сила давления на плечо при стрельбе из автомата, если масса пули равна 10г, а скорость пули при вылете из ствола равна 400м/с? Автомат делает 300 выстрелов в минуту.
3. Шар массой 3 кг движется со скоростью 4 м/с и ударяется о неподвижное тело такой же массы. Считая удар неупругим, найти количество теплоты, выделившейся при ударе.
4. Тело массой  , движущееся со скоростью , движущееся со скоростью  , налетает на неподвижное тело и после упругого соударения отскакивает от него под углом 900 к первоначальному направлению своего движения со скоростью , налетает на неподвижное тело и после упругого соударения отскакивает от него под углом 900 к первоначальному направлению своего движения со скоростью  /2. Определить массу /2. Определить массу 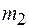 неподвижного тела. неподвижного тела.
5. Тело массой 1кг начинает движение из состояния покоя под действием постоянной силы, равной 10 Н. Каков будет импульс тела  , когда оно пройдет путь, равный 5м. , когда оно пройдет путь, равный 5м.
6. Шайбе, находящейся на плоскости, образующей с горизонтом угол  , сообщили начальную скорость , сообщили начальную скорость 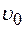 , направленную вдоль плоскости вверх. Угол наклона плоскости к горизонту, начиная с которого шайба скользит по плоскости, равен , направленную вдоль плоскости вверх. Угол наклона плоскости к горизонту, начиная с которого шайба скользит по плоскости, равен  С какой скоростью шайба вернется в исходную точку? С какой скоростью шайба вернется в исходную точку?
7. Мяч падает на пол с высоты  и отскакивает от него. Полагая, что при каждом ударе и отскакивает от него. Полагая, что при каждом ударе  я часть кинетической энергии переходит в тепло, определите: через какое время мяч остановится; путь, пройденный мячом за время движения. я часть кинетической энергии переходит в тепло, определите: через какое время мяч остановится; путь, пройденный мячом за время движения.
8. На легких стержнях длиной  висят два шара массами висят два шара массами  и 2 и 2  . Стержни могут вращаться свободно в вертикальной плоскости. Между шарами вставлена небольшая пружина с коэффициентом упругости . Стержни могут вращаться свободно в вертикальной плоскости. Между шарами вставлена небольшая пружина с коэффициентом упругости  . С какой силой нужно сжать пружину, чтобы при восстановлении деформации стержень с более легким шаром стал в вертикальное положение? Массой пружины пренебречь. . С какой силой нужно сжать пружину, чтобы при восстановлении деформации стержень с более легким шаром стал в вертикальное положение? Массой пружины пренебречь.
9. Два шара массами  и и 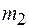 , летящие навстречу друг другу со скоростями , летящие навстречу друг другу со скоростями 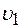 и и 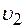 , сталкиваются, и происходит центральный упругий удар. , сталкиваются, и происходит центральный упругий удар.
а) Определите скорости шаров после соударения. б) Исследуйте полученный результат в зависимости от соотношения между массами и скоростями шаров, найдите условие, при котором происходит наибольшая передача кинетической энергии. в) Найдите импульс и энергию каждого шара в системе отсчета, связанной с их центром масс, суммарную кинетическую энергию шаров.
10. Три небольших гладких шара A, B и C лежат на одной прямой на расстоянии  друг от друга, их массы равны друг от друга, их массы равны  , ,  и и  . В некоторый момент времени шарам сообщают скорости в одном направлении, равные соответственно . В некоторый момент времени шарам сообщают скорости в одном направлении, равные соответственно  , 4 , 4  и и  . Шар В догоняет А и отлетает к С. Полагая соударение упругим, определите расстояние между шарами А и С в тот момент, когда шар подлетит к шару С. Каковы будут установившиеся скорости шаров А и С при . Шар В догоняет А и отлетает к С. Полагая соударение упругим, определите расстояние между шарами А и С в тот момент, когда шар подлетит к шару С. Каковы будут установившиеся скорости шаров А и С при 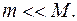
11. Тело массой  2кг движется со скоростью 2кг движется со скоростью 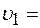 3м/с и нагоняет тело массой 3м/с и нагоняет тело массой  8кг, движущееся со скоростью 8кг, движущееся со скоростью 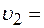 1м/с. Считая удар центральным, найти скорости 1м/с. Считая удар центральным, найти скорости  и и  тел после удара, если удар а) неупругий; б) упругий. тел после удара, если удар а) неупругий; б) упругий.
12. Тело массой  5кг ударяется о неподвижное тело массой 5кг ударяется о неподвижное тело массой  2,5кг, которое после удара начинает двигаться с кинетической энергией 2,5кг, которое после удара начинает двигаться с кинетической энергией  5Дж. Считая удар центральным и упругим, найти кинетическую энергию 5Дж. Считая удар центральным и упругим, найти кинетическую энергию  и и  первого тела до и после удара. первого тела до и после удара.
13. Два тела движутся навстречу друг другу и соударяются неупруго. Скорости тел до удара были 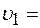 2м/с и 2м/с и 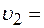 4м/с. Общая скорость тел после удара 4м/с. Общая скорость тел после удара  1м/с и по направлению совпадает с направлением скорости 1м/с и по направлению совпадает с направлением скорости 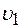 . Во сколько раз кинетическая энергия . Во сколько раз кинетическая энергия  первого тела была больше кинетической энергии первого тела была больше кинетической энергии  второго тела? второго тела?
14. Два шара с массами  0,2 кг и 0,2 кг и  0,1 кг подвешены на нитях одинаковой длины так, что они соприкасаются. Первый шар отклоняют на высоту 0,1 кг подвешены на нитях одинаковой длины так, что они соприкасаются. Первый шар отклоняют на высоту  4,5 см и отпускают. На какую высоту 4,5 см и отпускают. На какую высоту  поднимутся шары после удара, если удар: а) упругий; б) неупругий? поднимутся шары после удара, если удар: а) упругий; б) неупругий?
15. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня 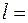 1 м. Найти скорость 1 м. Найти скорость  пули, если известно, что стержень с шаром отклонился от удара пули на угол пули, если известно, что стержень с шаром отклонился от удара пули на угол  100. 100.
16. Стальной шарик массой  20г, падая с высоты 20г, падая с высоты  1 м на стальную плиту, отскакивает от нее на высоту 1 м на стальную плиту, отскакивает от нее на высоту  81 см. Найти импульс силы 81 см. Найти импульс силы  , полученный плитой за время удара, и количество теплоты , полученный плитой за время удара, и количество теплоты  , выделившееся при ударе. , выделившееся при ударе.
17. Тело массы  бросили под углом бросили под углом  к горизонту с начальной скоростью к горизонту с начальной скоростью 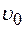 . Найти среднюю мощность, развиваемую силой тяжести за все время движения тела, и мгновенную мощность этой силы как функцию времени. . Найти среднюю мощность, развиваемую силой тяжести за все время движения тела, и мгновенную мощность этой силы как функцию времени.
18. Какую мощность развивают двигатели ракеты массы  , которая неподвижно висит над поверхностью Земли, если скорость истечения газов равна , которая неподвижно висит над поверхностью Земли, если скорость истечения газов равна 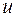 ? ?
19. Тело массы  начинают поднимать с поверхности Земли, приложив к нему силу начинают поднимать с поверхности Земли, приложив к нему силу  , которую изменяют с высотой подъема , которую изменяют с высотой подъема 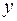 по закону по закону  где где  положительная постоянная. Найти работу этой силы и приращение потенциальной энергии тела в поле тяжести Земли на первой половине пути подъема. положительная постоянная. Найти работу этой силы и приращение потенциальной энергии тела в поле тяжести Земли на первой половине пути подъема.
20. Тонкая цепочка массы  25 г и длины 25 г и длины 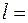 100 см лежит на столе в виде небольшой кучки. К одному из концов цепочки приложили направленную вертикально вверх силу 100 см лежит на столе в виде небольшой кучки. К одному из концов цепочки приложили направленную вертикально вверх силу  где где  0,47 Н/м, 0,47 Н/м,  высота подъема от поверхности стола. Найти скорость цепочки в момент отрыва ее нижнего конца от стола. высота подъема от поверхности стола. Найти скорость цепочки в момент отрыва ее нижнего конца от стола.
21. Потенциальная энергия частицы в некотором поле имеет вид: 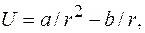 где где 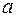 и и  положительные постоянные, положительные постоянные,  расстояние от центра поля. Найти: расстояние от центра поля. Найти:
а) значение  соответствующее равновесному положению частицы; выяснить, устойчиво ли это положение; соответствующее равновесному положению частицы; выяснить, устойчиво ли это положение;
б) максимальное значение силы притяжения; изобразить примерные графики зависимостей  и и 
22.  На Рис.2.5.3 показан школьный прибор для демонстрации сложения количеств движения, полученных шариком С при ударах молотков А и В. Показать, что путь, пройденный шариком С по горизонтальной плоскости при одновременном ударе молотков А и В, равен сумме путей, которые прошел бы шарик при таких же ударах молотков А и В по отдельности: На Рис.2.5.3 показан школьный прибор для демонстрации сложения количеств движения, полученных шариком С при ударах молотков А и В. Показать, что путь, пройденный шариком С по горизонтальной плоскости при одновременном ударе молотков А и В, равен сумме путей, которые прошел бы шарик при таких же ударах молотков А и В по отдельности: 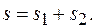
23. Показать, что изменение кинетической энергии при неупругом ударе зависит только от относительной скорости тел до удара и от их масс.
24. Молот массой 1,5  ударяет по раскаленной болванке, лежащей на наковальне, и деформирует болванку. Масса наковальни вместе с болванкой равна 20 ударяет по раскаленной болванке, лежащей на наковальне, и деформирует болванку. Масса наковальни вместе с болванкой равна 20  . Определить коэффициент полезного действия при ударе молота, считая удар неупругим. . Определить коэффициент полезного действия при ударе молота, считая удар неупругим.
25. Два стальных шара подвешены на нитях так, что при их касании центры тяжести находятся на 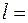 1 м ниже точек подвеса, а нити вертикальны. Массы их 1 м ниже точек подвеса, а нити вертикальны. Массы их  800 г и 800 г и  200 г. Меньший отводят в сторону так, что нить отклоняется на 200 г. Меньший отводят в сторону так, что нить отклоняется на  900, и отпускают. Принимая шары за вполне упругие, определить: а) на какую высоту они поднимутся после удара; б) что произойдет, если таким же образом отклонить больший шар; в) при каком соотношении между массами шаров высоты, на которые они поднимутся после удара, равны между собой. 900, и отпускают. Принимая шары за вполне упругие, определить: а) на какую высоту они поднимутся после удара; б) что произойдет, если таким же образом отклонить больший шар; в) при каком соотношении между массами шаров высоты, на которые они поднимутся после удара, равны между собой.
|
 1) Случай 1:
1) Случай 1:
 и
и 
 Дано:
m=50г=
h1=2м
h2=1м
Δt=0,02с
Дано:
m=50г=
h1=2м
h2=1м
Δt=0,02с

 ). На рисунке (б) изображены силы: действующие на мяч при ударе -
). На рисунке (б) изображены силы: действующие на мяч при ударе - 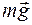 (сила тяжести) и
(сила тяжести) и  (сила реакции опоры), а также сила
(сила реакции опоры), а также сила  , действующая на пол со стороны мяча (сила удара мяча о пол – искомая сила).
, действующая на пол со стороны мяча (сила удара мяча о пол – искомая сила). и
и  равны:
равны: 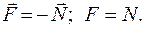
 и
и  ,
, – равнодействующая всех сил, действующих на мяч:
– равнодействующая всех сил, действующих на мяч: .
. ,
, и
и  начальная и конечная скорости по отношению к удару, а не ко всему движению, то есть
начальная и конечная скорости по отношению к удару, а не ко всему движению, то есть  скорость буквально перед ударом,
скорость буквально перед ударом,  .
. ,
, скорости
скорости  найдём, пользуясь формулами кинематики:
найдём, пользуясь формулами кинематики: ;
; 
 ;
; 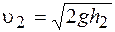
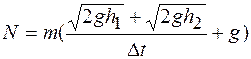
 .
. 27,5Н.
27,5Н. 27,5Н.
27,5Н. кг
кг

 .
.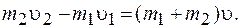
 :
: .
. .
.

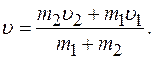
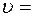 3 м/с.
3 м/с. и выражение для
и выражение для  1м/с.
1м/с. 500 кг
500 кг
 120 кг
120 кг
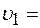 4 м/с
4 м/с
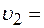 0
0

 , затраченная на деформацию, равна разности значений механической энергии системы до и после удара:
, затраченная на деформацию, равна разности значений механической энергии системы до и после удара: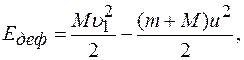 (1)
(1) общая скорость тел, входящих в систему, после неупругого удара.
общая скорость тел, входящих в систему, после неупругого удара. ,
,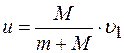 . (2)
. (2)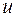 из (2), находим энергию деформации:
из (2), находим энергию деформации: .(3)
.(3) (4)
(4) 0,19.
0,19. , движущееся со скоростью
, движущееся со скоростью 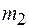 неподвижного тела.
неподвижного тела. , когда оно пройдет путь, равный 5м.
, когда оно пройдет путь, равный 5м. , сообщили начальную скорость
, сообщили начальную скорость 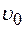 , направленную вдоль плоскости вверх. Угол наклона плоскости к горизонту, начиная с которого шайба скользит по плоскости, равен
, направленную вдоль плоскости вверх. Угол наклона плоскости к горизонту, начиная с которого шайба скользит по плоскости, равен  С какой скоростью шайба вернется в исходную точку?
С какой скоростью шайба вернется в исходную точку? и отскакивает от него. Полагая, что при каждом ударе
и отскакивает от него. Полагая, что при каждом ударе  я часть кинетической энергии переходит в тепло, определите: через какое время мяч остановится; путь, пройденный мячом за время движения.
я часть кинетической энергии переходит в тепло, определите: через какое время мяч остановится; путь, пройденный мячом за время движения. висят два шара массами
висят два шара массами  и 2
и 2  . С какой силой нужно сжать пружину, чтобы при восстановлении деформации стержень с более легким шаром стал в вертикальное положение? Массой пружины пренебречь.
. С какой силой нужно сжать пружину, чтобы при восстановлении деформации стержень с более легким шаром стал в вертикальное положение? Массой пружины пренебречь.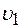 и
и 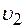 , сталкиваются, и происходит центральный упругий удар.
, сталкиваются, и происходит центральный упругий удар. и
и 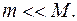
 2кг движется со скоростью
2кг движется со скоростью  8кг, движущееся со скоростью
8кг, движущееся со скоростью  и
и  тел после удара, если удар а) неупругий; б) упругий.
тел после удара, если удар а) неупругий; б) упругий. 5Дж. Считая удар центральным и упругим, найти кинетическую энергию
5Дж. Считая удар центральным и упругим, найти кинетическую энергию  и
и  первого тела до и после удара.
первого тела до и после удара. 1м/с и по направлению совпадает с направлением скорости
1м/с и по направлению совпадает с направлением скорости  второго тела?
второго тела? 4,5 см и отпускают. На какую высоту
4,5 см и отпускают. На какую высоту 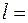 1 м. Найти скорость
1 м. Найти скорость  100.
100. 1 м на стальную плиту, отскакивает от нее на высоту
1 м на стальную плиту, отскакивает от нее на высоту  81 см. Найти импульс силы
81 см. Найти импульс силы  , полученный плитой за время удара, и количество теплоты
, полученный плитой за время удара, и количество теплоты  , выделившееся при ударе.
, выделившееся при ударе.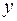 по закону
по закону  где
где  положительная постоянная. Найти работу этой силы и приращение потенциальной энергии тела в поле тяжести Земли на первой половине пути подъема.
положительная постоянная. Найти работу этой силы и приращение потенциальной энергии тела в поле тяжести Земли на первой половине пути подъема. где
где  высота подъема от поверхности стола. Найти скорость цепочки в момент отрыва ее нижнего конца от стола.
высота подъема от поверхности стола. Найти скорость цепочки в момент отрыва ее нижнего конца от стола.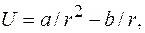 где
где 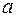 и
и  положительные постоянные,
положительные постоянные,  расстояние от центра поля. Найти:
расстояние от центра поля. Найти: соответствующее равновесному положению частицы; выяснить, устойчиво ли это положение;
соответствующее равновесному положению частицы; выяснить, устойчиво ли это положение; На Рис.2.5.3 показан школьный прибор для демонстрации сложения количеств движения, полученных шариком С при ударах молотков А и В. Показать, что путь, пройденный шариком С по горизонтальной плоскости при одновременном ударе молотков А и В, равен сумме путей, которые прошел бы шарик при таких же ударах молотков А и В по отдельности:
На Рис.2.5.3 показан школьный прибор для демонстрации сложения количеств движения, полученных шариком С при ударах молотков А и В. Показать, что путь, пройденный шариком С по горизонтальной плоскости при одновременном ударе молотков А и В, равен сумме путей, которые прошел бы шарик при таких же ударах молотков А и В по отдельности: