|
|
Статистичні методи аналізу взаємозв’язківЗавдання 1. Лінійний однофакторний кореляційно-регресійний аналіз
Мета завдання: Навчитися досліджувати взаємозв’язки за допомогою застосування кореляційно-регресійного аналізу Зміст завдання: У відповідності із варіантом завдання за даними аналітичного групування побудувати емпіричну лінію регресії, яка характеризує кореляційний зв’язок: a) між віком і розміром заробітної плати робітника; b) між кваліфікаційним розрядом і розміром заробітної плати робітника; c) між загальним трудовим стажем робітника і розміром його заробітної плати; d) між неперервним стажем роботи працівника на даному підприємстві та розміром його заробітної плати; e) між загальним трудовим стажем робітника і його кваліфікаційним розрядом; f) між неперервним стажем роботи працівника на даному підприємстві та його кваліфікаційним розрядом. Таблиця 5.1 Вибір варіантів завдання
& Одним із найважливіших завдань статистики є дослідження характеру взаємозв’язків між різними соціально-економічними явищами, що мають причинно-наслідковий характер. Ознаки, що характеризують причини та умови зв’язку, називають факторними ознаками ”x”, а ті, що характеризують наслідки – результативними ознаками ”y”. Між ознаками x та y виникають різні за природою та характером зв’язки, зокрема функціональні та стохастичні. При функціональному зв’язку кожному значенню ознаки х відповідає одне чітко визначене значення ознаки у. При стохастичному зв’язку кожному значенню ознаки х відповідає певна множина значень у, які утворюють так званий умовний розподіл. Вивчення стохастичних зв’язків є досить складним завданням, тому в статистичних дослідженнях, як правило, замінюють умовний розподіл середньою величиною Одним із методів дослідження кореляційного зв’язку є кореляційно-регресійний аналіз. У цій моделі аналізу кореляційний зв’язок задається теоретичною лінією регресії (рівнянням). Рівняння регресії – це аналітична функція, яка описує залежність результативної ознаки від факторної. При виборі форми рівняння регресії важливим є якісний аналіз досліджуваних явищ. Найпоширенішою та найпростішою в статистичному аналізі формою рівняння регресії є лінійна однофакторна функція Y = a + bx. Параметр b – коефіцієнт регресії вказує на скільки одиниць в середньому зміниться у із зміною х на одиницю. Він має одиницю виміру результативної ознаки. Параметр a називають вільним членом рівняння регресії, тобто це значення у при х = 0. Якщо х не набуває нульових значень, цей параметр має лише розрахункове призначення. Знаходження параметрів рівняння регресії базується на методі найменших квадратів. Параметри a і b лінійного однофакторного рівняння визначаються із системи нормальних рівнянь, яка для не згрупованих даних записується як:
Якщо дані згруповані, наприклад, представлені у вигляді аналітичного групування, то система нормальних рівнянь має наступний вигляд:
Тобто при побудові системи нормальних рівнянь за згрупованими даними застосовуються зважені з допомогою частот суми значень ознак, їх квадратів і добутків. Щільність кореляційного зв’язку оцінюють за допомогою коефіцієнта детермінації R2, який розраховується за формулою:
де - для не згрупованих даних - для згрупованих даних як
R2 змінюється від 0 до 1 і показує, яка частина загальної варіації результативної ознаки зумовлена факторною ознакою, а яка – зумовлена іншими факторами, не врахованими при побудові рівнянні регресії. При R2 = 1 рівняння регресії проходить через усі емпіричні точки і встановлює точну відповідність між значеннями ознаки х і значеннями ознаки у. Тобто у цьому випадку між ознаками х та у існує функціональний зв’язок. R2 = 0 є свідченням відсутності зв’язку, вираженого даним рівнянням регресії. При використанні коефіцієнта детермінації слід враховувати, що дисперсія теоретичних значень Для дослідження лінійного зв’язку використовують також лінійний коефіцієнт кореляції (Пірсона), який доцільно обчислювати за формулою:
Цей коефіцієнт змінюється від -1 до +1 і дозволяє оцінити як щільність кореляційного зв’язку, так і його напрям. Напрям визначається знаком коефіцієнта кореляції Пірсона (”+” – прямий, ”-” – обернений). При |r = 1| існує лінійна функціональна залежність, при r = 0 – зв’язок відсутній. Чим ближчий r за своїм абсолютним значенням до 1, тим вища щільність зв’язку, чим ближчий до 0, тим вона нижча. Грубою помилкою є розрахунок коефіцієнта кореляції між середніми значеннями факторної і результативної ознак, представленими в аналітичній груповій таблиці. Як правило, величина лінійного коефіцієнта кореляції, розрахованого таким чином, близька до одиниці, тоді як дійсна степінь щільності і зв’язку може бути значно нижчою. Перевірка істотності зв’язку здійснюється шляхом порівняння фактичного значення R2 з його критичним значенням R21-α (k1,k2) (визначається за таблицями з додатку Д). k1 і k2 – ступені вільності, які обчислюються наступним чином:
де m – кількість параметрів теоретичного рівняння регресії, n – кількість елементів сукупності. Якщо фактичне значення R2 більше за критичне, то зв’язок між результативною та факторною ознакою вважається істотним. Якщо фактичне значення R2 менше, ніж критичне, то наявність кореляційного зв’язку між ознаками не доказана і зв’язок вважається неістотним. Перевірку істотності зв’язку з використанням F-критерію (критерію Фішера) проводять шляхом порівняння фактичного значення F-критерію з його критичним (табличним) значенням. Фактичне значення F-критерію розраховується за формулою:
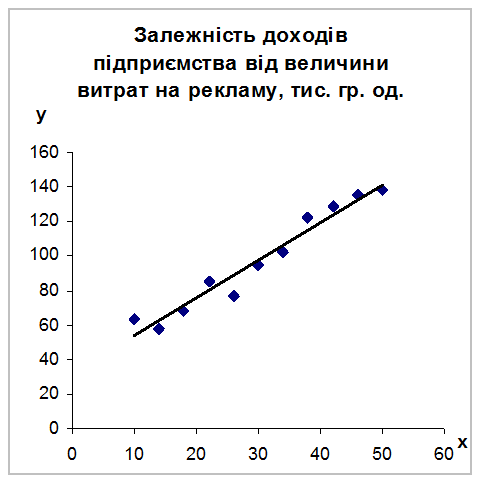
Критичне значення позначається F1-α( k1; k2) і визначається на основі таблиці Додатку Г. Якщо фактичне значення F-критерію більше за критичне, то це свідчить про істотність зв’язку. Якщо ж фактичне значення F-критерію менше за критичне, то істотність зв’язку не доведена. На рис. 5.1 представлений приклад графічного зображення теоретичної лінії регресії та емпіричних даних, що відображають зв’язок між витратами підприємства на рекламу та його доходами.
Рис. 5.1. Приклад графічного зображення теоретичної лінії регресії та емпіричних даних
Послідовність виконання завдання: 1. Відповідно до індивідуального завдання для двох заданих ознак побудувати вихідну таблицю статистичних даних у вигляді таблиці 5.2. Таблиця 5.2 Вихідна таблиця статистичних даних
2. Сформувати таблицю впорядкованих даних, результати представити в табл. 5.3. Таблиця 5.3 Таблиця впорядкованих даних
2. Провести аналітичне групування статистичних даних, результати якого представити у вигляді таблиці 5.4. Таблиця 5.4 Аналітичне групування для дослідження кореляційного зв’язку між ознаками (вказати назви ознак)
3. Обчислити параметри рівняння регресії, яке відображає залежність між факторною та результативною ознаками. Записати вид отриманого рівняння регресії. 4. За допомогою коефіцієнта детермінації оцінити щільність кореляційного зв’язку. 5 Перевірити істотність зв’язку за допомогою критичних значень коефіцієнта детермінації R2 та F-критерію (критерію Фішера) при α = 0,05. 6. Зобразити графічно теоретичну лінію регресії та емпіричні дані у вигляді точок. 7. За результатами дослідження зробити висновки про взаємозв’язок між досліджуваними ознаками.
GКонтрольні питання 1. Які ознаки називаються факторними? Які ознаки називаються результативними? 2. Які особливості функціонального та стохастичного зв’язку? 3. Який зв’язок називається кореляційним? 4. Що таке рівняння регресії? 5. Для чого використовується коефіцієнт детермінації? Який діапазон його значень? 6. В чому полягають особливості використання та суть лінійного коефіцієнта кореляції? 7. Як здійснюється перевірка істотності зв’язку з використанням F-критерію?
|
|
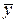 , в результаті чого утворюється різновид стохастичного зв’язку – кореляційний зв’язок.
, в результаті чого утворюється різновид стохастичного зв’язку – кореляційний зв’язок.

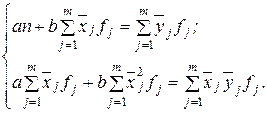 (5.2)
(5.2) ,
,
 – дисперсія теоретичних значень, яку ще називають факторною і обчислюють
– дисперсія теоретичних значень, яку ще називають факторною і обчислюють ;
; ;
; – загальна дисперсія.
– загальна дисперсія. характеризує не всю варіацію результативної ознаки у, пов’язану з варіацією факторної ознаки х, а лише ту її частину, яка відповідає теоретичному рівнянню регресії. Тому коефіцієнт детермінації в кореляційно-регресійному аналізі є фактично показником якості апроксимації вибраною теоретичною лінією регресії кореляційного зв’язку між ознаками.
характеризує не всю варіацію результативної ознаки у, пов’язану з варіацією факторної ознаки х, а лише ту її частину, яка відповідає теоретичному рівнянню регресії. Тому коефіцієнт детермінації в кореляційно-регресійному аналізі є фактично показником якості апроксимації вибраною теоретичною лінією регресії кореляційного зв’язку між ознаками.



 2fj
2fj