Изменения температуры жидкости от времени нагрева

(количества теплоты, переданной жидкости при нагреве)

1. Система действий по получению и обработке результатов измерения времени нагрева жидкости до определенной температуры и изменения температуры жидкости:

1) проверить, нужно ли ввести поправку; если да, то ввести поправку;

2) установить, сколько измерений данной величины нужно произвести;

3) подготовить таблицу для записи и обработки результатов наблюдений;

4) произвести установленное число измерений данной величины; результаты наблюдений занести в таблицу;

5) найти измеренное значение величины как среднее арифметическое результатов отдельных наблюдений с учетом правила запасной цифры:

6) вычислить модули абсолютных отклонений результатов отдельных измерений от среднего:

7) найти случайную погрешность;

8) найти инструментальную погрешность;

9) найти погрешность отсчета;

10) найти погрешность вычисления;

11) найти полную абсолютную погрешность;

12) записать результат с указанием полной абсолютной погрешности.

2. Система действий по построению графика зависимости Δt = f(Δτ):

1) начертить координатные оси; ось абсцисс обозначить Δτ, с, а ось ординат – Δt, ⁰С;

2) выбрать масштабы для каждой из осей и нанести на осях шкалы;

3) изобразить интервалы значений Δτ и Δt для каждого опыта;

4) провести плавную линию так, чтобы она проходила внутри интервалов.

3. ОИ № 1 – вода массой 100 г при начальной температуре 18 ⁰С:

1) для измерения температуры будем использовать термометр со шкалой до 100 ⁰С; для измерения времени нагрева будем пользоваться шестидесятисекундным механическим секундомером. Эти приборы не требуют внесения поправок;

2) при измерении времени нагрева до фиксированной температуры возможны случайные погрешности. Поэтому проведем 5 измерений промежутков времени при нагревании до одной и той же температуры (в расчетах это утроит случайную погрешность). При измерении температуры случайных погрешностей не обнаружено. Поэтому будем считать, что абсолютная погрешность при определении t, ⁰C равна инструментальной погрешности используемого термометра, то есть цене деления шкалы 2 ⁰С (табл. 3);

3) составим таблицу для записи и обработки результатов измерений:

4) результаты проведенных измерений занесены в таблицу;

5) среднее арифметическое каждого измерения τ вычислено и указано в последней строке таблицы;

6) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для температуры 25 ⁰C:

7) находим случайную погрешность измерения:

8) инструментальную погрешность секундомера в каждом случае находим с учетом полных кругов, сделанных секундной стрелкой (то есть если один полный круг дает погрешность 1,5 с, то полкруга дает 0,75 с, а 2,3 круга – 3,45 с). В первом опыте Δt_и = 0,7 c;

9) погрешность отсчета механического секундомера принимаем равной одному делению шкалы: Δt_о = 1,0 с;

10) погрешность вычисления в данном случае равна нулю;

11) рассчитываем полную абсолютную погрешность:

Δt = Δt_C + Δt_и + Δt₀ + Δt_B = 4,44 + 0,7 + 1,0 + 0 = 6,14 с ≈ 6,1 с;

(здесь окончательный результат округлен с недостатком до одной значащей цифры);

12) записываем результат измерения: t = (27,4 ± 6,1) с

6 а) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для температуры 40 ⁰С:

7 а) находим случайную погрешность измерения:

8 а) инструментальная погрешность секундомера во втором опыте
Δt_и = 2,0 c;

9 а) погрешность отсчета механического секундомера Δt_о = 1,0 с;

10 а) погрешность вычисления в данном случае равна нулю;

11 а) рассчитываем полную абсолютную погрешность:

Δt = Δt_C + Δt_и + Δt₀ + Δt_B = 8,88 + 2,0 + 1,0 + 0 = 11,88 с ≈ 11,9 с;

12 а) записываем результат измерения: t = (86,2 ± 11,9) с

6 б) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для температуры 55 ⁰С:

7 б) находим случайную погрешность измерения:

8 б) инструментальная погрешность секундомера в данном опыте
Δt_и = 3,5 c;

9 б) погрешность отсчета механического секундомера Δt_о = 1,0 с;

10 б) погрешность вычисления в данном случае равна нулю;

11 б) рассчитываем полную абсолютную погрешность:

Δt = Δt_C + Δt_и + Δt₀ + Δt_B = 6,72 + 3,5 + 1,0 + 0 = 11,22 с ≈ 11,2 с;

12 б) записываем результат измерения: t = (146,8 ± 11,2) с

6 в) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для температуры 70 ⁰С:

7 в) находим случайную погрешность измерения:

8 в) инструментальная погрешность секундомера в данном опыте
Δt_и = 5,0 c;

9 в) погрешность отсчета механического секундомера Δt_о = 1,0 с;

10 в) погрешность вычисления в данном случае равна нулю;

11 в) рассчитываем полную абсолютную погрешность:

Δt = Δt_C + Δt_и + Δt₀ + Δt_B = 7,92 + 5,0 + 1,0 + 0 = 13,92 с ≈ 13,9 с;

12 в) записываем результат измерения: t = (206,8 ± 13,9) с

6 г) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для температуры 85 ⁰С:

7 г) находим случайную погрешность измерения:

8 г) инструментальная погрешность секундомера в данном опыте
Δt_и = 6,4 c;

9 г) погрешность отсчета механического секундомера Δt_о = 1,0 с;

10 г) погрешность вычисления в данном случае равна нулю;

11 г) рассчитываем полную абсолютную погрешность:

Δt = Δt_C + Δt_и + Δt₀ + Δt_B = 4,8 + 6,4 + 1,0 + 0 = 12,2 с;

12 г) записываем результат измерения: t = (269,0 ± 12,2) с

6 д) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для температуры 100 ⁰С:

7 д) находим случайную погрешность измерения:

8 д) инструментальная погрешность секундомера в данном опыте
Δt_и = 8,0 c;

9 д) погрешность отсчета механического секундомера Δt_о = 1,0 с;

10 д) погрешность вычисления в данном случае равна нулю;

11 д) рассчитываем полную абсолютную погрешность:

Δt = Δt_C + Δt_и + Δt₀ + Δt_B = 5,28 + 8,0 + 1,0 + 0 = 14,28 с ≈ 14,3 с;

12 д) записываем результат измерения: t = (328,2 ± 14,3) с.

Результаты расчетов представим в виде таблицы, в которой приводятся разности конечной и начальной температуры в каждом опыте и время нагрева воды.

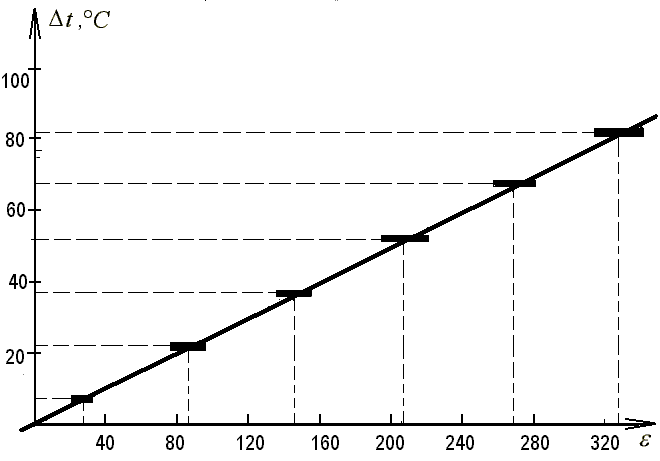
4. Построим график зависимости изменения температуры воды от количества теплоты (времени нагрева) (рис. 14). При построении во всех случаях указывается интервал погрешности измерения времени. Толщина линии соответствует погрешности измерения температуры.

Рис. 14. График зависимости изменения температуры воды от времени ее нагрева

5. Устанавливаем, что полученный нами график похож на график прямой пропорциональной зависимости y = kx. Значение коэффициента k в данном случае нетрудно определить из графика. Поэтому окончательно можно записать Δt = 0,25Δτ. Из построенного графика можно сделать вывод, что температура воды прямо пропорциональна количеству теплоты.

6. Повторяем все измерения для ОИ № 2 – подсолнечного масла.
В таблице, в последней строке, приведены средние результаты.

6) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для температуры 25 ⁰С:

1) находим случайную погрешность измерения:

2) инструментальную погрешность секундомера в каждом случае находим так же, как и в первой серии опытов. В первом опыте Δt_и = 0,3 c;

3) погрешность отсчета механического секундомера принимаем равной одному делению шкалы: Δt_о = 1,0 с;

4) погрешность вычисления в данном случае равна нулю;

5) рассчитываем полную абсолютную погрешность:

Δt = Δt_C + Δt_и + Δt₀ + Δt_B = 2,64 + 0,3 + 1,0 + 0 = 3,94 с ≈ 3,9 с;

6) записываем результат измерения: t = (10,4 ± 3,9) с

6 а) Рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для температуры 40 ⁰С:

7 а) находим случайную погрешность измерения:

8 а) инструментальная погрешность секундомера во втором опыте
Δt_и = 0,8 c;

9 а) погрешность отсчета механического секундомера Δt_о = 1,0 с;

10 а) погрешность вычисления в данном случае равна нулю;

11 а) рассчитываем полную абсолютную погрешность:

Δt = Δt_C + Δt_и + Δt₀ + Δt_B = 3,12 + 0,8 + 1,0 + 0 = 4,92 с ≈ 4,9 с;

12 а) записываем результат измерения: t = (36,8 ± 4,9) с

6 б) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для температуры 55 ⁰С:

7 б) находим случайную погрешность измерения:

8 б) инструментальная погрешность секундомера в данном опыте
Δt_и = 1,5 c;

9 б) погрешность отсчета механического секундомера Δt_о = 1,0 с;

10 б) погрешность вычисления в данном случае равна нулю;

11 б) рассчитываем полную абсолютную погрешность:

Δt = Δt_C + Δt_и + Δt₀ + Δt_B = 3,84 + 1,5 + 1,0 + 0 = 6,34 с ≈ 6,3 с;

12 б) записываем результат измерения: t = (61,6 ± 6,3) с

6 в) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для температуры 70 ⁰С:

7 в) находим случайную погрешность измерения:

8 в) инструментальная погрешность секундомера в данном опыте
Δt_и = 2,1 c;

9 в) погрешность отсчета механического секундомера Δt_о = 1,0 с;

10 в) погрешность вычисления в данном случае равна нулю;

11 в) рассчитываем полную абсолютную погрешность:

Δt = Δt_C + Δt_и + Δt₀ + Δt_B = 2,52 + 2,1 + 1,0 + 0 = 5,62 с ≈ 5,6 с;

12 в) записываем результат измерения: t= (87,2 ± 5,6) с

6 г) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для температуры 85 ⁰С:

7 г) находим случайную погрешность измерения:

8 г) инструментальная погрешность секундомера в данном опыте
Δt_и = 2,7 c;

9 г) погрешность отсчета механического секундомера Δt_о = 1,0 с;

10 г) погрешность вычисления в данном случае равна нулю;

11 г) рассчитываем полную абсолютную погрешность:

Δt = Δt_C + Δt_и + Δt₀ + Δt_B = 4,56 + 2,7 + 1,0 + 0 = 8,26 с ≈ 8,3;

12 г) записываем результат измерения: t = (112,6 ± 8,3) с

6 д) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для температуры 100 ⁰С:

7 д) находим случайную погрешность измерения:

8 д) инструментальная погрешность секундомера в данном опыте
Δt_и = 3,4 c;

9 д) погрешность отсчета механического секундомера Δt_о= 1,0 с;

10 д) погрешность вычисления в данном случае равна нулю.

11 д) рассчитываем полную абсолютную погрешность:

Δt = Δt_C + Δt_и + Δt₀ + Δt_B = 5,28 + 3,4 + 1,0 + 0 = 9,68 с ≈ 9,7 с;

12 д) записываем результат измерения: t = (137,8 ± 9,7) с.

Результаты расчетов представим в виде таблицы, в которой приводятся разности конечной и начальной температуры в каждом опыте и время нагрева подсолнечного масла.

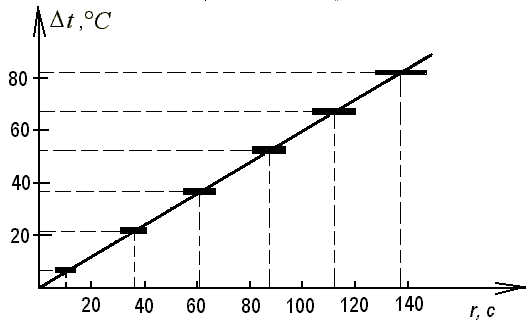
7. Построим график зависимости изменения температуры масла от времени нагрева (рис. 15). При построении во всех случаях указывается интервал погрешности измерения времени. Толщина линии соответствует погрешности измерения температуры.

Рис. 15. График зависимости изменения температуры воды от времени ее нагрева

8. Построенный график похож на график прямой пропорциональной зависимости y = kx. Значение коэффициента k в данном случае нетрудно найти из графика. Поэтому окончательно можно записать Δt = 0,6Δτ.

Из построенного графика можно сделать вывод, что температура подсолнечного масла прямо пропорциональна количеству теплоты.

9. Формулируем ответ на ПЗ: температура жидкости прямо пропорциональна количеству теплоты, полученному телом при нагревании.

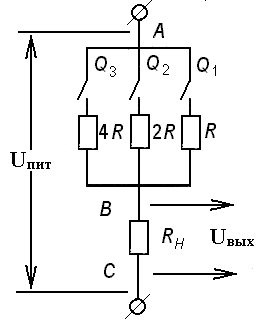
Пример 3. ПЗ: установить вид зависимости выходного напряжения на резисторе R_н от значения эквивалентного сопротивления участка цепи АВ (задача решается на экспериментальной установке, принципиальная схема которой приведена на рис. 16).

Для решения этой задачи нужно выполнить следующие действия.

1. Составить систему действий по получению и обработке результатов измерения эквивалентного сопротивления участка цепи и напряжения на нагрузке R_н (см. п. 2.2.8 или п. 2.2.9).

2. Составить систему действий по построению графика зависимости выходного напряжения (на резисторе R_н) от эквивалентного сопротивления участка цепи АВ.

3. Выбрать ОИ № 1 – участок с определенным значением R_н1 и выполнить все запланированные в п. 1 и 2 действия.

4. Подобрать известную в математике функциональную зависимость, график которой похож на экспериментальную кривую.

5. Записать математически эту функциональную зависимость для нагрузки R_н1 и сформулировать для нее ответ на поставленную познавательную задачу.

6. Выбрать ОИ № 2 – участок ВС с другим значением сопротивления R_н2 и выполнить с ним ту же систему действий.

7. Подобрать известную в математике функциональную зависимость, график которой похож на экспериментальную кривую.

8. Записать математически эту функциональную зависимость для сопротивления R_н2 и сформулировать для него ответ на поставленную познавательную задачу.

9. Сформулировать функциональную зависимость между величинами в обобщенном виде.

Отчет о выявлении вида зависимости выходного напряжения на сопротивлении R_н от эквивалентного сопротивления участка цепи АВ

(приводится в сокращенном варианте)

Независимой переменной величиной является эквивалентное сопротивление участка цепи АВ, которое измеряется с помощью цифрового вольтметра, подключаемого к точкам А и В схемы. Измерения проводились на пределе 1000 Ом, то есть точность измерений равна цене младшего разряда, что соответствует ±1 Ом.

Зависимой переменной являлось значение выходного напряжения, снимаемого на сопротивлении нагрузки (точки В и С). В качестве измерительного прибора использовался цифровой вольтметр с минимальным разрядом сотые доли вольта.

Рис. 16. Схема экспериментальной установки для исследования вида зависимости выходного напряжения от величины эквивалентного сопротивления цепи

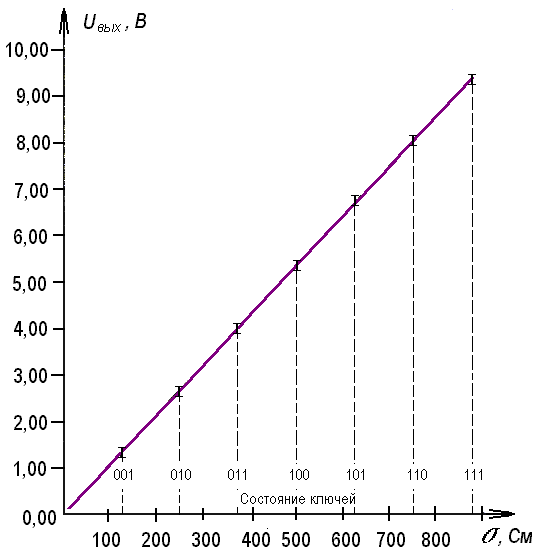
Эквивалентное сопротивление менялось с помощью ключей Q₁, Q₂ и Q₃. Для удобства включенное состояние ключа будем обозначать «1», а выключенное – «0». В данной цепи возможно всего 8 их комбинаций.

Для каждой комбинации выходное напряжение измерялось 5 раз.

В ходе исследования были получены следующие результаты:

Результаты обработки экспериментальных данныхприведены в следующей таблице:

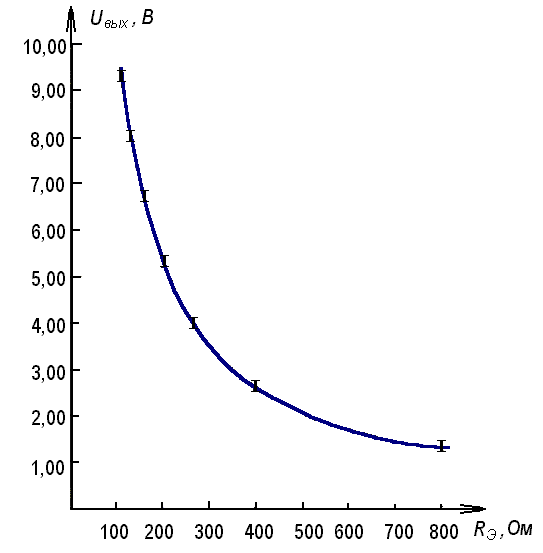
Строим график зависимости выходного напряжения от значения эквивалентного сопротивления U = f(R_Э).

При построении графика длина линии соответствует погрешности измерения ΔU, индивидуальной для каждого опыта (максимальная погрешность ΔU = 0,116 В, что соответствует примерно 2,5 мм на графике при выбранном масштабе). Толщина линии соответствует погрешности измерения эквивалентного сопротивления. Получившийся график представлен на рис. 17.

Рис. 17. График зависимости выходного напряжения

от значения эквивалентного сопротивления на участке АВ

График напоминает график обратной пропорциональной зависимости. Для того чтобы убедиться в этом, построим график зависимости выходного напряжения от величины, обратной значению эквивалентного сопротивления U = f(1/R_Э),то есть от проводимости σ цепи. Для удобства данные для этого графика представим в виде следующей таблицы:

Полученный график (рис. 18) подтверждает высказанное предположение: выходное напряжение на сопротивлении нагрузки R_н1 обратно пропорционально эквивалентному сопротивлению участка цепи АВ: U = 0,0017/R_Э.

Выбираем другой объект исследования: ОИ № 2 – другое значение сопротивления нагрузки R_н2, и выполняем все те же действия. Получаем аналогичный результат, но с другим коэффициентом k.

Формулируем ответ на ПЗ: выходное напряжение на сопротивлении нагрузки R_н обратно пропорционально значению эквивалентного сопротивления участка цепи, состоящего из трех параллельно соединенных проводников, которые можно включать в одной из восьми комбинаций.

Рис. 18. График зависимости выходного напряжения от проводимости участка цепи АВ

Отметим, что рассматриваемая схема является цифро-аналоговым преобразователем (ЦАП) – устройством, переводящим цифровой код (в данном случае двоичный) в аналоговый сигнал (в данном случае – в напряжение).

Планирование деятельности по решению познавательной задачи № 4

Экспериментальное нахождение конкретного значения конкретной физической величины (решение познавательной задачи № 4) может осуществляться в двух ситуациях: 1) метод нахождения указанной физической величины неизвестен и 2) метод нахождения данной величины уже разработан. В первой ситуации возникает потребность в разработке метода (системы действий) и подборе оборудования для его практической реализации. Во второй ситуации возникает потребность изучить этот метод, то есть выяснить, какое оборудование должно быть использовано для практической реализации этого метода и какова должна быть система действий, последовательное выполнение которых позволит получить конкретное значение конкретной величины в конкретной ситуации. Общим для обеих ситуаций является выражение искомой величины через другие величины, значение которых можно найти прямым измерением. Говорят, что в этом случае человек осуществляет косвенное измерение.

Значения величин, полученные косвенным измерением, являются неточными. Это и понятно: они находятся по результатам прямых измерений, которые всегда неточны. В связи с этим в систему действий по решению познавательной задачи № 4 обязательно должны входить действия по расчету погрешностей.

Для нахождения погрешностей косвенных измерений разработано два метода: метод границ погрешностей и метод границ. Рассмотрим содержание каждого из которых.

Метод границ погрешностей

Метод границ погрешностей основан на дифференцировании.

Пусть косвенно измеряемая величина у является функцией нескольких аргументов: y = f(X₁, X₂, …, X_N).

Величины Х₁, Х₂, ..., Х_n измерены прямыми методами с абсолютными погрешностями ΔХ₁, ΔХ₂, …, ΔХ_N. Вследствие этого величина у будет найдена также с некоторой погрешностью Δу.

Обычно ΔX₁ << Х_1,, ΔХ₂ << Х₂, …, ΔХ_N << Х_n, Δy << у. Поэтому можно перейти к бесконечно малым величинам, то есть заменить ΔХ₁, ΔХ₂, …, ΔХ_N, Δy их дифференциалами dХ₁, dХ₂, ..., dХ_N, dy соответственно. Тогда относительная погрешность

относительная погрешность функции равна дифференциалу ее натурального логарифма.

В правую часть равенства вместо дифференциалов переменных величин подставляют их абсолютные погрешности, а вместо самих величин – их средние значения. С целью определения верхней границы погрешности алгебраическое суммирование погрешностей заменяют арифметическим.

Зная относительную погрешность, находят абсолютную погрешность

Δу = ε_уּу,

где вместо у подставляют полученное в результате измерения значение

У_изм = f (<Х₁>, <Х₂>, ..., <Х_n>).

Все промежуточные расчеты выполняют по правилам приближенных вычислений с одной запасной цифрой. Конечный результат и погрешности округляют по общим правилам. Ответ записывают в виде

У =У_изм ± ΔУ; ε_у = …

Выражения для относительных и абсолютных погрешностей зависят от вида функции у. Основные, часто встречающиеся при выполнении лабораторных работ формулы представлены в таблице 5.

Таблица 5