|
|
Электролитпен коагуляциялау кинетикасы 3 глава2 - саты ол электролиттердің әсерінен болатын кәдімгі коагуляция, мұнда әрине эквиваленттік сақталмайды. Шульце-Гарди ережесін тек осы саты үшін ғана қолдануға болады. Әрине бұл айтылған теорияның бәрі коагуляцияны сапалық түрде ғана сипаттайды. Коагуляцияны сандық түрде сипаттайтын теорияны жасауда және коагуляция механизмін түсіндіруге Б.В.Дерягиннің жұмыстарының маңызы зор. Енді соған тоқталайық.
6.Лиофобтық кірнелердің тұрақтылығының теориясы – ДЛФО теориясы Тұрақтылықтың қазіргі теориясын ресейлік ғалымдар Б.В.Дерягин және Л.Д.Ландау, сәл кейінірек голландиялық ғалымдар Фервей мен Овербек жасаған. Сондықтан тұрақтылықтың қазіргі теориясын осы ғалымдардың фамилияларының бас әріптерімен атап ДЛФО теориясы деп атайды. Коллоидтық бөлшектер бір біріне өте жақындағанда олардың диффузиялық қабаттары бір бірін жауып, әрекеттеседі. Бұл әрекеттесу бөлшектерді бөліп тұратын дисперстеуші ортаның жұқа қабатында болады. Лиофобтық кірнелердің тұрақтылығы негізінен осы жұқа сұйық қабаттың ерекше қасиеттерімен анықталады. Дисперстеуші ортадағы екі коллоидтық бөлшек бір біріне жақындағанда алғашқы кезде оларды сұйықтықтың қалың қабаты бөліп тұрады; ол қабат біртіндеп жұқара береді де, нәтижесінде өте жұқа қабатқа айналады. Өте жұқа қабат түзілгеннен кейін оның жұқаруы әрі қарай жалғаса беруі мүмкін, ол бөлшектерді одан әрі қарай жақындатады. Сұйық қабаттың жұқаруы иә оның қалыңдығы өте аз болғанда, иә әрі қарай кішіреймейтін қандай да бір тепе-теңдік қалыңдықта аяқталады. Бірінші жағдайда бөлшектер бір-бірімен бірігеді, ал екінші жағдайда бірікпейді. Жұқа сұйық қабаттың қасиетері коагуляцияның болу-болмауын, яғни кірнелердің тұрақтылығын анықтайды. Зерттеулер бөлшектердің өзара жақындағанда жұқа қабаттың жұқаруы одан сұйықтықтың шығып кетуінен болады. Сұйық қабат айтарлықтай жұқа болғанда (оның қалыңдығы 100-200 нм-ден аз болғанда), ондағы сұйықтықтың қасиеттері қоршаған көллемдегі сұйықтық қасиеттерінен өте күшті өзгере бастайды. Осы кезде қабатта қосымша қысым пайда болады, оны Б.В.Дерягин «сыналық қысым» деп атады. Дерягиннің анықтамасы бойынша қабаттағы қысым төмендесе оң таңбалы болады, ол қабаттан сұйықтықтың шығып кетуіне кері әсер етеді, яғни коллоидтық бөлшектердің бірігуіне кедергі жасайды. Сол себептен «сыналық қысым» деп атаған, яғни бөлшектерді біріктірмей қозғалтады, сыналайды. Сыналық қысымның таңбасы теріс болуы мүмкін, яғни қабатта қысым көбейеді, ол қабаттан сұйықтықтың шығып кетуін жылдамдатады және бөлшектердің бірігуін де жылдамдатады. Осы жұқа қабатта сыналық қысымның пайда болуына негізінен екі фактор әсер етеді: 3) Қабаттағы электростатикалық әрекеттесу – ол энергиясы Uтб>0 тебілу күштері 4) Энергиясы Uтр˂0 ван-дер-ваальстік тартылу күштері Бөлшекаралық әрекеттесудің шешуші энергиясы U деп екі құрамдастың сомасы (қосындысы) ретінде анықталады: U = Uтб + (-Uтр) = Uтб – Uтр Екі |Uтб|>|Uтр| болса, онда тебілу күштері басым болғандықтан коагуляция болмайды, кірне агрегаттық тұрақты болады. Керісінше жағдайда тартылу күші басым болғандықтан бөлшектер бірігіп коагуляция болады. Осы күштерді сандық түрде түсіндіріп көрейік.
Тебілудің электростатикалық күштері Мицеллалар арасындағы электростатикалық тебілу қарсы иондардың диффузиялық қабаттары бір-бірін жапқанда пайда болады. Ол әрекеттесудің энергиясы былайша анықталады: Uтб = A*e-ϰh (16) мұндағы: h – бөлшектердің ара қашықтығы; ϰ=1/δ – ол диффузиялық қабат қалыңдығына δ кнрі шама; А - ол h-қа тәуелсіз, ҚЭҚ параметрлерімен анықталатын шама. Κ және A шамаларын ҚЭҚ теориясының негізінде есептеуге болады. Есептеулер тебілу энергиясының (Uтб) қарсы иондардың зарядтары мен концентрациялары артқанда және φ0-мен ξ-потенциалдарының абсолюттік шамалары төмендегенде азаятынын көрсетті. (16) теңдеуден Uтб бөлшектердің ара қашықтығы h артқан сайын экспоненциалды түрде өседі. (2-сурет)
Тартылудың ван-дер-ваальстік күштері Тартылу энергиясы, негізінен, молекулалар арасындағы дисперсиялық әрекеттесумен байланысты. Оны мына теңдеумен есептеуге болады: Uтр = -Ar / 48πh2 (17) мұндағы Ar – Гамакер коснтантасы, ол 10-12 эрг-ке тең. Ол кванттық-статикалық жолмен есептелген және оған коагуляциялық және адгезиялық әрекеттесулердің жеке константалары кіреді. (17)-теңдеуден тартылу энергиясы бөлшектердің арақашықтығы (h) артқан сайын қашықтық квадратына кері пропорционалды түрде өзгертетіні көрініп тұр. Сонымен, тартылу қашықтығына байланысты баяу төмендейді екен. Мысалы: h 100 есе артқанда тартылу энергиясы 104 есе азаяды, ал тебілу энергиясы 1043 есе азаяды. Арақашықтығы h бөлшектердің арасындағы шешуші әрекеттесу энергиясы мына теңдеумен анықталады: U(h) = A * e-ϰh – Ar/48πh2 (18) Тебілу энергиясы мен тартылу энергиясының h-қа байланысты өзгеру сипаты әртүрлі болғандықтан бөлшектер арасының қашықтығына байланысты шешуші потенциалдық энергияның өзгеруі күрделі сипатта болады. Осы тәуелділіктің U=f(h) жалпы түрі 2-суретте көрсетілген.
2-сурет. Екі коллоидтық бөлшектің әрекеттесуінің потенциалдық энергиясы Екінші суреттегі графиктің үш аймағына жеке-жеке тоқталайық: 4) ˂h˂h1, U(h)˂0 бұл кезде бөлшектің арасында тартылу күштері басым болады, жақын минимум (шұңқыр) байқалады. Uтб → тұрақты, Uтр → ∞ Бұл кезде коагуляция болады. 5) h1˂h˂h2, U(h)>0. Бұл кезде бөлшектер арасында тебілу күштері басым болады, яғни Uтб>|Uтр|. Бұл кезде бөлшектер бірікпейді. 6) h2˂h˂h3, U(h)˂0 – бұл кезде қашық минимум (шұңқыр) байқалады, алайда оның тереңдігі онша емес Үш жағдайда h=h1, h=h2, h=h3 U(h) = 0 болады, яғни осы арақашықтықтарда тебілу күштер мен тартылу күштері өзара тең. Сонымен, енді бөлшектер h1 қашықтыққа жақындаса, онда олар бір бірімен бірігеді екен, алайда ол үшін потенциалдық тосқауылды жеңу керек. Ол бөлшектердің кинетикалық энергиясы (КТ) айтарлықтай көп болуы керек. Екі бөлшектің әрекеттесуін қарастырайық. Бір бөлшекті қозғалмайды, ал екінші бөлшек оған қарай КТ энергиясымен жақындайды деп есептейік. Егер KT˂ΔUmin болса, бөлшектер hmin қашықтығында қалады және бір бірімен дисперстеуші орта қабаты арқылы байланысқан болады, яғни «жұп» түзеді, бірақ тікелей бірікпейді және өзінің седиментациялық тұрақтылығын жоғалтпайды. Бұндай жағдайларда қашық минимумдегі әрекеттесу деп атайды. Егер ΔUmin˂KT˂ΔUk болса, онда бөлшектер бір-бірімен соқтығысқанда бір-бірімен бірікпей, керісінше жан-жаққа ұшады. Жүйе агрегаттық тұрақты болады. Егер KT˂ΔUk болса, онда баяу коагуляция, ал егер KT>ΔUk болса, онда жылдам коагуляция болады. Әдетте зольді тұрақты (бөлмелік) температурада қарастыратындықтан бөлшектердің кинетикалық энергиясы тұрақты болады. Ендеше, коагуляция болу үшін потенциалдық тосқауылды азайту керек. Әдетте потенциалдық тосқауылды азайту үшін жүйеге электролит-коагулянт енгізеді. ДЛФО теориясы жылдам коагуляция табалдырығы Сжк есептеуге мүмкіндік береді: Cжк = B*E(KT)5/A2*e6z6 (19) мұндағы: A, B – есептеуге болатын тұрақты шамалар; E – ортаның диэлектрлік өтімділігі; z – ион-коагулянт заряды; e – элеткрон заряды. Бұл формуладан ДЛФО теориясы бойынша қорытылған коагуляция табалдырығының ион-коагулянт зарядының тәуелділігі Шульце-Гардидің эмпирикалық ережесіне сәйкес келетін болжауға болады: Сшк = B*
Электролиттік коагуляция түрлері Зольдерді электролиттермен коагуляциялағанда екі түрлі коагуляция болады: концентрациялық коагуляция және бейтараптану коагуляциясы. Концентрациялық коагуляуцияиндеференттік электрлиттің әсерінен болады; ол кезде қарсы иондардың диффузиялық қабат қысылу салдарынан ζ-поетнциалының абсолюттік мәні азаяды. Күміс нитратымен тұрақтанған хлорлы күміс кірнесіне калий нитратын қосқандағы концентрациялық коагуляцияны қарастырайық. Ол кірненің мицелласының формуласын былай жазуға болады:
3- суретте күміс хлориді мицелласының ҚЭҚ-тың потенциал өзгерісінің графигі көрсетілген.
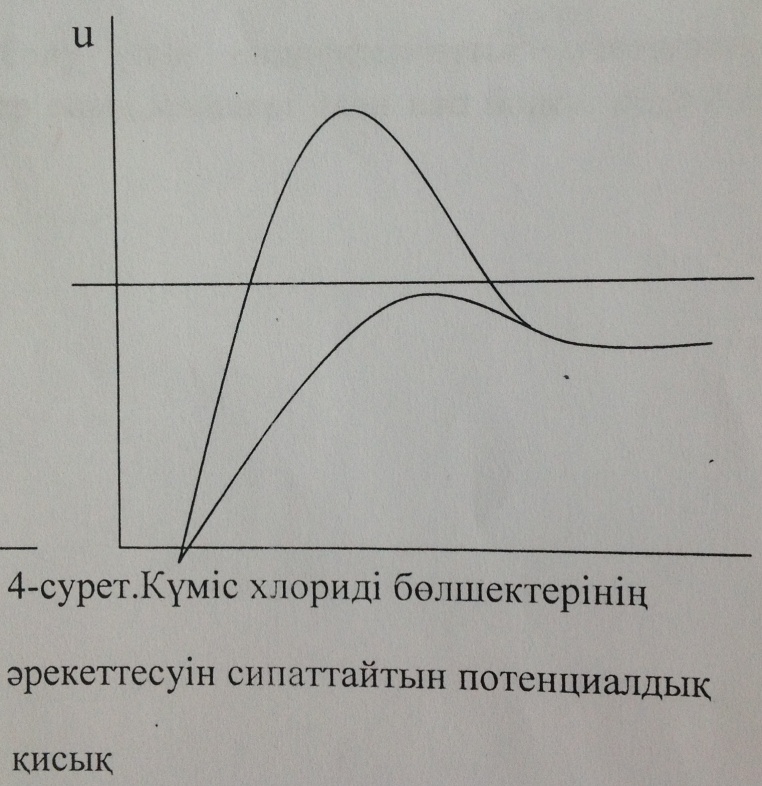
3- сурет. Күміс хлориді мицелласының 4-сурет. Күміс хлориді бөлшектерінің ҚЭҚ-тың потенциал өзгерісі әрекеттесуінің сипаттайтын потенциалдық қисық
Ондағы 1- қисық бастапқы мицеллаға, ал 2-қисық күміс нитратының коагуляция болдыратындай мөлшерде қосқаннан кейінгі жағдайға тән қисықтар. Күміс нитратын қосқанда қарсы иондардың диффузиялық қабаты қысылады да, мицелланың формуласы мынадай болады: 4-суретте осы кірнедегі бөлшектердің әрекеттесуін сипаттайтын потенциалдық қисықтар берілген. Бастапқы коллоидтық бөлшектің Бейтараптану коагуляциясы кірнеге индиференттік емес электролит қосқанда болады. Фаянс-Панет ережесі бойынша бұл кезде потенциал анықтағыш иондар қиын еритінқосылыстарға айналып, термодинамикалық потенциалдың ( Бастапқы кірне ретінде қарастырған
Жүйеде Бұл жолы коагуляция себебі потенциал анықтағыш иондардың бейтараптануы болғандықтан, мұндай коагуляцияны бейтараптану коагуляциясы деп атайды. Толық бейтараптану коагуляциясы болу үшін индифференттік емес электролит тек эквивалентті мөлшерде қосылуы керек. Егер оның мөлшері одан көп болса, онда “қайта зарядталу” құбылысы болады.
Коллоидтық жүйелердің тұрақтылығы мен коагуляциясының қазіргі теориясы (ДЛФО теориясы) Қазіргі кезде жалпыға бірдей қабылданған электролиттік коагуляцияның жалпы теориясы — ол статикалық физиканың жалпы принциптеріне, ерітінділер теориясына және молекулалық күштердің әсерінің теориясына негізделе отырып жасалған коагуляцияның физикалық теориясы. Бұл теория бөлшектердің арасындағы молекулалық тарту және электростатикалық тебу күштерінің баланстарын қарастыра отырып электролиттік коагуляцияны түсіндірді. Коагуляцияның механизмін түсіндіруде Дерягин және оның қызметкерлерінің «сыналық қысым» туралы ілімінің мәні зор. Олардың пікірі бойынша электролиттердің коагуляцияға әсері потенциалдың азаюының нәтижесінде тебу күштердің азаюынан емес, коагулятордың әсерінен қабаттың қүрылысының өзгеруінен және диффузиялық бөлігінің азаюынан болатын диффузиялық иондардың гидраттық қабаттарының механикалық тұрақтылығының (сыналық қысымның азаюымен) азаюымен түсіндіріледі. Коагуляцияны сандық түрде сипаттауды алғаш 30-шы жылдарда Дерягин бастап, 1941 ол Ландаумен бірігіп коагуляцияның сандық теориясын жасады. Осы сияқты көзқараста голандиялық зерттеушілер Фервей мен Овербек те болды, олар бұл теорияны одан әрі дамытты. Сондықтан коагуляцияның физикалық теориясы осы кезде сол авторлардың фамилияларының алғашқы әріптерімен басталады (ДЛФО). Коагуляцияны қарастырғанда мынандай шекті екі жағдайда айту керек: 1. бейтараптану коагуляциясы бұл коллоидтық бөлшектер зарядтарының бейтараптануы нәтижесінде 2. концентрациялық коагуляция қабаттың қысылуының нәтижесінде болады. Коагуляцияның осы екі түріне жеке-жеке тоқталайық. Бейтараптану коагуляциясы.Бұл зольдердің бөлшектерінің зарядтары аз болғанда болатын коагуляция. Ендеше ондай кірнелерде Дерягиннің теориясы бойынша
с - константа, А-тарту тұрақтылығы, ξ - ерітіндінің диэлектрлік тұрақтылығы. Бұндағы
1.13 – сурет. 1.14 – сурет.
1.15 – сурет. В-тәжірибе арқылы табылатын шама. Егер жүйе тұрақсыз, яғни коагуляция болады, егер Концентрациялық коагуляция.Бұл бөлшектердің зарядтары көп (әдетте 100 мв – тан көп) болғанда индиференттік электролиттердің концентрациясы өскен кезде байқалған (1.14 - сурет). Мұндай коагуляция кезінде Дерягин мен Ландау энергетикалық тосқауылдың болмайтынына сәйкес келетін коцентрацияны (коагуляция табалдырығын) теориялық жолмен мына формула бойынша анықтауға болатынын көрсетті:
С–электролиттің ассиметриясы , яғни катион мен анион зарядтардың қатысына аздап байланысты болатын константа. е – электрон заряды, z – қарсы ионның валенттілігі. Бұдан концентрациялық коагуляцияның Жоғары теңдеудегі барлық тұрақты шамаларды α деп алатын болсақ , онда мынадай теңдеуді жазуға болады : γ=α/Z6 бұдан Шульце-Гардидің эмпирикалық ережесін ДЛФО теориясы бойынша негіздеуге болатындығын көреміз. Үшінші тарау. Коллоидтық жүйелердің құрылымды - механикалық қасиеттері 3.1 Дисперстік жүйелерді зерттеудің реологиялық әдістері
Физикалық денелердің (қатты денелер мен түрлі материалдардың) негізгі қасиеттері – олардың механикалық қасиеттері: беріктілік, серпімділік, эластикалылық, пластикалылық және тұтқырлық. Бұл қасиеттер дененің құрылымымен – олардың ішіндегі молекулалық байланысу күштерінің және молекулалардың жылулық қозғалыстарының ерекшеліктерімен байланысты, сондықтан оларды жалпы құрылымды-механикалық қасиеттер деп атайды. Қатты дененің құрылымы дегеніміз тек кристалдық тордың құрылысы ғана емес, сонымен қатар поликристалдық дененің дисперстік құрылымы, және де бір-бірімен молекулалық байланысқан атомдар, иондар, молекулалар немесе коллоидтық бөлшектерден түзілген құрылымдар. Мұнда қатты дененің құрылымы жеке бөлшектің – монокристалдың кристалдық торының құрылысымен ғана сипатталып қоймай, оның жеке бөлшегінің шамасымен де, сол бөлшектің өлшемі бойынша таралу сипатымен, қатты денеде ақаулардың болуымен және ақаулардың таралуымен де сипатталады. Жүйелердің құрылымды-механикалық қасиеттерін реология әдістерімен зерттейді. «Реология» атауы негізінен, гректің «ρεοσ» - «ағу» және «λογοσ» - «ілім» деген сөздерінен пайда болған. Дененің деформациясы деп – жүйенің біртұтастығы бұзылмастан басқа нүктемен салыстырмалы ығысуын айтады.Деформация қайтымды және қайтымсыз (қалдықты) болуы мүмкін. Қайтымды деформацияға серпімді деформациялар жатады. Қайтымсыз деформация тұтқыр (кез келген кернеу Р мәніндегі) ағуға және пластикалық (кейбір даңдарыстық мәндерден асқан кернеу Р мәндеріндегі) ағуға тең. Серпімді деформациялармен қатар көлемдік (созылу, сығылу), ығысу және айналу деформациясы деп бөлінеді. Олар сандық түрде өлшемсіз шамалармен сипатталады. Бірөлшемді деформациялану кезінде созылу салыстырмалы ұзару шамасымен сипатталады:
мұнда l0 және l – дененің созылғанға дейінгі және одан кейінгі ұзындығы, сәйкесінше Δl – абсолютті ұзару. Ығысу деформациясы Р кернеуінің әсерінен болған салыстырмалы ығысумен анықталады: немесе (2)
мұнда y – жоғарғы қабаттың ығысуы, x – ығыстырылған қабаттың қалыңдығы. Деформацияның түрі әсер еткен кернеу Р түріне байланысты. Денені деформацияға ұшыратқан кернеу (жүктеме) Р әсер еткен кернеудің ауданына қатысты күшімен анықталады. Әсер еткен күш бетке перпендикулярлы (қалыпты) және тангенсиалды, яғни бетке жанамалай бағытталған болуы мүмкін. Сәйкесінше кернеудің екі түрі бар: қалыпты және тангенсиалды. Әрине, бұларға екі негізгі деформациялар сәйкес: созылу (немесе сығылу) және ығысу. Кернеудің өлшем бірлігі ӨЖ (СИ) жүйесі бойынша – Па (паскаль), ал СГС бойынша – дин/см2. Дисперсті жүйелерді зерттеу кезінде көбінде ығысу деформациясы қолданылады. Реологияда дененің механикалық қасиеттерін үлгілер арқылы сипаттайды. Серпімді, тұтқыр және пластикалық қасиеттер бір элементтен тұратын қарапайым реологиялық үлгілермен бейнеленеді: идеал серпімді Гук денесі, идеал тұтқыр Ньютон денесі және идеал пластикалық Сен-Венан-Кулон денесі. |
|


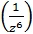
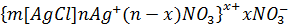

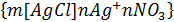
 -потенциалы оң болады, ол потенциалдық тосқауыл
-потенциалы оң болады, ол потенциалдық тосқауыл  (1- қисық) жасайды. Сондықтан коллоидтық бөлшектер соқтығысқанда бірін бірі тебеді де, коагуляция болмайды. Калий нитратын қосқаннан кейін
(1- қисық) жасайды. Сондықтан коллоидтық бөлшектер соқтығысқанда бірін бірі тебеді де, коагуляция болмайды. Калий нитратын қосқаннан кейін  (2- қисық). Сондықтан коллоидтық бөлшектердің жақындауына ешнәрсе кедергі жасамайды, олар соқтығысып бірігеді, яяғни коагуляция болады. Қарастырған жағдайда коагуляцияның себебі қарсы иондар концентрацияның артуы болғандықтан, оны концентрациялық коагуляция деп атайды.
(2- қисық). Сондықтан коллоидтық бөлшектердің жақындауына ешнәрсе кедергі жасамайды, олар соқтығысып бірігеді, яяғни коагуляция болады. Қарастырған жағдайда коагуляцияның себебі қарсы иондар концентрацияның артуы болғандықтан, оны концентрациялық коагуляция деп атайды.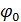 ) абсолюттік мәні азаяды, ендеше,
) абсолюттік мәні азаяды, ендеше,  кірнесін алсақ, онда потенциал анықтағыш иондарды
кірнесін алсақ, онда потенциал анықтағыш иондарды  бейтараптау үшін кірнеге, мысалы, калий хлоридін енгізу керек. Осы индифференттік емес электролиттің белгілі- бір мөлшерін қосқаннан кейінгі мицелланың формуласы былай болады:z
бейтараптау үшін кірнеге, мысалы, калий хлоридін енгізу керек. Осы индифференттік емес электролиттің белгілі- бір мөлшерін қосқаннан кейінгі мицелланың формуласы былай болады:z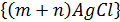
 кеміп,жүйенің түрақтылығын жоғалтуы.
кеміп,жүйенің түрақтылығын жоғалтуы. кемуінен емес, диффузиялық
кемуінен емес, диффузиялық (ол энергетикалық тосқауыл болмайтын потенциал) диффузиялық қабаттың қалыңдығы (һ) арасындағы байланысты былай көрсетуге болады:
(ол энергетикалық тосқауыл болмайтын потенциал) диффузиялық қабаттың қалыңдығы (һ) арасындағы байланысты былай көрсетуге болады: 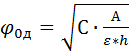
 мен һ-тың арасындағы байланысты 1940 ж Эйлерс пен Корф эмпирикалық түрде былайша көрсеткен :
мен һ-тың арасындағы байланысты 1940 ж Эйлерс пен Корф эмпирикалық түрде былайша көрсеткен :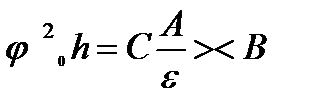

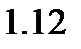 - сурет.
- сурет.


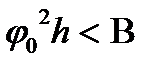 болса, онда
болса, онда болса, онда жүйе тұрақты болады. Егер өте сұйылтылған болса, онда диффузиялық қабат қалың болады да ,
болса, онда жүйе тұрақты болады. Егер өте сұйылтылған болса, онда диффузиялық қабат қалың болады да ,  мәні
мәні  мәніне жақын болады. Алайда
мәніне жақын болады. Алайда  орнына
орнына  потенциалдың мәнін алу дұрыс емес, ондай есептеулер дұрыс мәліметтер бермейді.
потенциалдың мәнін алу дұрыс емес, ондай есептеулер дұрыс мәліметтер бермейді.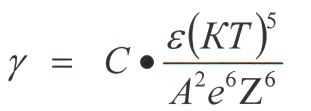
 байланыстылығын көруге болады.
байланыстылығын көруге болады. (1)
(1)
