|
|
Электролитпен коагуляциялау кинетикасы 4 главаИдеал серпімді Гук денесіқарапайым серіппемен (1,а-сурет), деформация шамасы Гук заңымен анықталады:
немесе (3) мұнда Р - қалыпты (созылу) кернеу, γ – салыстырмалы созылу деформациясы, Е – серпімділік модулі. Юнг модулі Е осы теңдеудің пропорционалдық коффициенті болып табылады және материал қаттылығын сипаттайды. Юнг модулі Р=f(γ) қисығының көлбеуінің тангенс бұрышы α мәніне тең. Гук заңынан серпімді дененің деформациясы γ оған әсер еткен кернеудің шамасына тура пропорционал екені көрінеді. (1,ә-сурет). Идеал серпімді дененің деформациясы толық қайтымды, яғни кернеудің әсері жойылғаннан кейін дененің деформациясы толығымен жойылады.
Идеал тұтқыр Ньютон денесі идеал тұтқыр сұйықтықпен толтырылған ішінде поршені бар цилиндрден тұрады (2,а сурет). Деформация жылдамдығы, яғни цилиндрдің қозғалу жылдамдығы бұл үлгіде Ньютон заңымен сипатталады:
немесе (4)
мұнда Р – жанама күш кернеуі, γ'=f(P) қисығының координаталар басынан шығатын түзу Ньютон заңына сәйкес екені анық. Мұнда dγ/dτ осі жағындағы көлбеудің тангенс бұрышы η-қа тең, ал Р осі жағындағы тангенс бұрышының шамасы аққыштыққа 1/h тең (2,ә сурет). Ньютон сұйықтықтарының тұтқырлығы жүктемеге тәуелсіз. Кернеудің тұрақты шамасындағы (Р=const) деформация әсер етуші кернеудің уақытына пропорционал (2,б - сурет):
Түзудің τ осі жағындағы көлбеудің тангенс бұрышының tga мәні Р/η тең.
Идеал пластикалық Сен-Венан-Кулон денесі бетте сырғитын қатты денеден тұрады (3,а – сурет). Бұл дененің бет бойынша қозғалысы «құрғақ үйкеліс» заңына сәйкес және белгілі бір шекті кернеу Рт мәніне (аққыштық шегіне) тең. Идеал пластикалық дененің құрылымы деформация кезінде бұзылады да, оның кернеуге қарсы әсері толық жойылады. Сонымен пластикалық дененің деформациялық сипаты келесі шартпен орындалады:
және (6)
Серпімді, тұтқыр және пластикалық қасиеттері бар реал дененің күрделі реологиялық сипаты қарапайым реологиялық үлгілерден (Гук, Ньютон және Сен-Венан-Кулон үлгілері) бір-бірімен тізбектеп және параллельді жалғастырылған жинақтармен сипатталынады. Осы үш үлгі идеал серпімді денені, идеал тұтқыр сұйықты және идеал пластикалық денені суреттейді. Бұл қарапайым үлгілерді тізбектеп және параллель қоса отырып, параметрлері реал дененің қасиеттеріне жақын күрделі үлгіні алуға болады. Тізбектеп байланысқан элементтердің күш кернеулері мынадай:
Бұның деформациясы элементтердің деформацияларының қосындыларына тең:
Деформация жылдамдықтары да осы элементтердің деформация жылдамдықтарының қосындыларына тең:
Осы элементтерді параллельді жалғағанда кернеулердің қосындысы алынады:
Деформация шамасы сол элементтердің деформация шамаларына тең:
Деформация жылдамдығының мәні де сол элементтердің деформация жылдамдықтарының мәніне тең:
Гук және Ньютон (серпімді және тұтқыр) элементтерін тізбектеп жалғаса, серпімдітұтқыр дененің қасиеттерін сипаттайтын, яғни сұйықтың серпімді қасиетін ескеретін Максвелл үлгісін береді. Гук және Ньютон элементтерін тізбектеп жалғаса, үлгінің екі құрамдасына бірдей күш (ығысу кернеуі) әсер етеді:
Ал, деформациялары мен деформация жылдамдықтарының мәндері қосылады:
мұнда γ – жалпы деформация; γг – серпімді элементтің деформациясы; γН – тұтқыр элементтің деформациясы. (14) және (15) теңдеулерге сәйкесінше (3) және (4) теңдеулерді қойсақ, мынадай теңдеу аламыз:
немесе
(17) теңдеу Максвелл үлгісінің математикалық өрнегі болып табылады. Осы үлгілердің деформациясының кернеудің әсер ету уақытына тәуелділігі 4,ә суретте келтірілген.
Тұрақты кернеудің Р әсерінен алғашқыда Максвелл үлгісінің Гук элементі деформацияланады (лездік қайтымды деформация - γсерп), ал содан соң Ньютон элементінің деформациясымен анықталатын тұтқыр ағу басталады (қайтымсыз деформация – γпл). Жүктің әсері жойылғаннан кейін (Р=0) серпімді деформация жоғалады да, қайтымсыз деформациясы γпл сақталады. γсерп шамасын қолданып серпімділік модулінің өрнегін былай жазуға болады:
Ал қайтымсыз деформация γпл бойынша динамикалық тұтқырлықты (dγ/dτ=const кезіндегі) табуға болады:
γ=const және dγ/dτ=0 болғанда (17) теңдеуден мынаны аламыз:
мұнда Р0 – бастапқы кернеу, λ= η1/E1 – кернеудің релаксация уақыты. λ – шамасы тұрақты деформация кезіндегі бастапқы Р0 кернеудің е есе азаятынын көрсететін уақыт шамасына тең. λ шамасы көп болған сайын серпімдітұтқыр дененің кернеуінің релаксация уақыты да ұзақ. Бұл жерде кернеу релаксациясын 4,б - сурет сипаттайды. (23) теңдеуге сәйкес серпімдітұтқыр дененің реологиялық сипаты күштің әсер еткен уақытына τ және релаксация уақытына λ тәуелді. Егер λ<<t болса, яғни ығысу кернеуінің әсер еткен уақытымен салыстырғанда релаксация уақыты аз болса, жүйе сұйықтың сипатына ие болады және оның ағуы кезінде Р шамасы азаяды. Кернеудің толық релаксациясы τ→∞ жағдайда ғана жүзеге асады. Ал λ>>τ жағдайда жүйе қасиеті жағынан серпімді қатты денеге жақындайды. Бұл жағдайда кернеу релаксацияланып үлгермейді және бастапқы кернеу Р0 барлық уақыт (τ) аралығында сақталады. Релаксация функциясы бір экспоненциалдық қосылғышпен сипатталатын сұйықтық Максвелл сұйығы деп аталады. Кельвин-Фойгт үлгісі – бұл тұтқырсерпімді денені сипаттайтын эластикалылық қасиеті бар параллельді жалғанған Гук және Ньютон денелерінен тұратын жинақ (5,а - сурет). Бұл денеде серпімді деформация лезде пайда болмайды, тек Ньютон үлгісін деформациялауға қажетті уақыт өткенде ғана серпімді деформация жүзеге асады. Максвелл үлгісінен Кельвин-Фойгт үлгісінің айырмашылығы – серпімді пружинаны және тұтқыр элементті параллель жалғағанда олардың деформациясы және деформация жылдамдықтары бір-біріне тең, ал ығысу кернеулері қосылады:
мұнда РГ және РН –серпімді және тұтқыр элементтердің ығысу кернеулері. Осыдан:
(27) теңдеу Кельвин-Фойгт үлгісінің математикалық өрнегі болып табылады. Кельвин-Фойгт үлгісінің деформациясы Р=const, Р=Р0 жағдайда 5,ә - суреттегідей уақыт аралығында бірқалыпты өзгеріп отырады. Бұл кездегі үлгі деформациясының жылдамдығы мынаған тең:
Тұрақты кернеудің Р0 әсерінен Ньютон элементі қозғалысқа ұшырайды, бірақ белгілі бір уақыт өткен соң оның қозғалысы тежеледі, себебі серпімді элементке барынша көп күш кете бастайды. Деформация жылдамдығы нөлге ұмтылғанда үлгі деформациясы пружинаның серпімділік модулімен анықталатын максималды мәніне жетеді. Тұтқырсерпімді дененің уақытқа тәуелді деформациясын өрнектей алу үшін (28) теңдеуді интегралдаймыз. Кернеудің тұрақтылығын ескерсек, мынаны аламыз:
Мұнда θ=η2/Е2 – деформацияның релаксация уақыты немесе серпімділіктен кейінгі өзгерісітің уақыты; ол дененің эластикалылығын сипаттайды. θ шамасы өскен сайын оның эластикалылығы да жақсы байқалынады. Тұтқырсерпімді дененің эластикалылығының сипаты ретінде басқа да параметр – эластикалық деформация модулі Е2 қолданылады. Ол белгілі кернеу әсерінен болған барынша максималды деформация γэ шамасы бойынша анықталады.
Эластикалық деформация механикалық қайтымды болады. Деформацияланған тұтқырсерпімді жүйеден кернеудің әсерін жойса, ол бастапқы күйіне баяу қайтып келеді. Сонымен бірге, деформацияның жылдамдығы бір мәнге жеткенде уақыт өте келе азаяды (5,ә - суреттегі Р=0 кезіндегі деформация қисығы). Бұл үдеріс – серпімділіктен кейінгі өзгеріс - (29) теңдеуге ұқсас, тек бұл жағдайда бос мүшесі (Р=0) жоқ:
мұнда γ0 – кернеудің әсері тоқтаған кездегі деформация. Серпімділіктен кейінгі өзгеріс жүйенің эластикалылығымен де байланысты және деформацияның ұзақтығы релаксация уақытына θ тәуелді. (31) теңдеуге сәйкес жоғарыэластикалық денелерде деформация шамасы шексіз ұзақ уақыт аралығында толық жоғалады. Сондықтан оларда кез келген уақытта да қалдық деформация болады. Бингам үлгісі – үш реологиялық элементтерден құралған комбинация, ол параллельді қосылған Ньютон, Сен-Венан-Кулон және соңынан жалғанған Гук элементтерінен тұрады (6,а сурет). Бұл үлгі материалдың серпімді-тұтқыр-пластикалық қасиеттерін сипаттайды. Бұл үлгінің реологиялық қисықтары 6,ә және 6,б суреттерде көрсетілген.
Жалпы серпімдіпластикалық дене және тұтқырпластикалық орта деп ажыратылады. Мұнда серпімдіпластикалық денелер Гук заңына сәйкес белгілі бір критикалық жағдайға (ағу шегі) жеткенде деформацияланады; содан соң материал тұтқыр сұйықтық сияқты «ағады», яғни деформация уақытқа тәуелді сызықты өседі (Сен-Венан-Кулон үлгісі). Тұтқырпластикалық орта – бұл әсер етуші кернеудің мәні белгілі бір критикалық кернеуге – ағу шегіне Рт – жеткенше ешқандай деформацияға ұшырамайды, содан соң тұтқыр сұйық сияқты ағады. Р>Рт кезіндегі тұтқырпластикалық дене үлгісінің математикалық өрнегі Шведов-Бингам теңдеуімен өрнектеледі:
η* - (бингам) пластикалық тұтқырлығы.
Кернеу екі құраушыға бөлінеді: Рт – құрылымды бұзуға қажетті кернеу және Р-Рт – ағуды қамтамасыз ететін кернеу. Р<Рт кезіндегі деформация жылдамдығы нөлге тең (6, б сурет), Р>Рт кезінде кернеудің өсуімен ол да өседі. Рт=0 болғанда (32) теңдеу Ньютон заңына ауысады. Пластикалық тұтқырлық Р=Рт нүктесінен шығатын түзудің көлбеуінің α бұрышының котангенсімен анықталады. Ньютон сұйықтығы дененің ағуының барлық түрлерін ескереді. Пластикалық тұтқырлық Ньютон тұтқырлығының бір бөлігі болып табылады, сонымен бірге құрылымның бұзылу жылдамдығын көрсетеді, құрылымның беріктілігін ескермейді:
Басқа да күрделі үлгілер белгілі. Мысалы, Максвелл және Кельвин-Фойгт үлгілерін алма-кезек жалғастырғанда (7,а - сурет) серпімділік деформациясы, эластикалылығы бар, сонымен қатар релаксациялануға қабілетті кернеуі бар жүйе пайда болады. Мұндай құрамдас үлгінің деформациялық қисығы 7,ә - суретте көрсетілген. Математикалық түрде бұл үлгі келесі теңдеумен сипатталады (Р = const кезінде):
мұндағы
мұнда γ –салыстырмалы толық деформация; γо – лездік эластикалық деформация; γ1 – баяу эластикалық деформация; γпл – пластикалық деформация Көптеген фазааралық полимерлік қабыршақтардың деформациялық қисықтары 7,ә - суреттегі деформациялық қисыққа ұқсас болуы мүмкін. Тұрақты ығысу кернеуі әсерінен уақытқа тәуелді деформация өзгерісін көрсететін деформация қисықтарын γ=f(t) (34) теңдеуі арқылы өңдеп жүйенің құрылымдық-механикалық константаларын анықтауға болады. (34) теңдеу Максвелл-Шведов-Кельвин үлгісінің реологиялық қасиетін сипаттайтын математикалық теңдеу. Құрылымданған қойыртпақтың, полимерлік қабыршақтың механикалық қасиеттері бір-бірінен тәуелсіз бес константамен сипатталады: 1. Серпімділік (ығысу) модулі Е1, (Н/м2, дин/см2) немесе шартты-лездік серпімділік модулі
мұнда а – масса қабатының қалыңдығы. Бұл модуль лездік эластикалық деформацияға γ0 сәйкес. 2. Эластикалық модуль
мұнда γm – максимальды деформация және баяу эластикалық деформацияға γ1 сәйкес. 3. Тепе-теңдік модулі
бұл толық дамыған эластикалық деформацияға сәйкес. 4. Пластикалық тұтқырлық
мұнда Р- 5. Ағудың нақты шегі РК1, (Н/м2, дин/см2)
Ағудың нақты шегінен аз кернеулерде серпімділік, серпімділіктен кейінгі өзгеріс және ньютондық аса тұтқырлығы бар баяу ағу байқалады. Тәжірибелерден алынған константаларды пойдаланып құрылымдық-механикалық сипаттамаларды табуға болады: 1. Максвелл релаксация периоды 2. Эластикалылық |
|


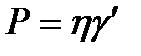
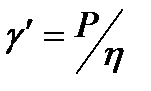
 - деформация жылдамдығы, η – тұтқырлық коэффициенті (тұтқырлық), τ – деформация уақыты.
- деформация жылдамдығы, η – тұтқырлық коэффициенті (тұтқырлық), τ – деформация уақыты. (5)
(5) жағдайда
жағдайда 
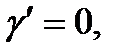
 жағдайда
жағдайда 
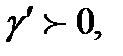
 (7)
(7) (8)
(8)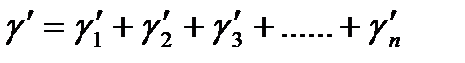 (9)
(9) (10)
(10)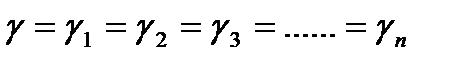 (11)
(11) (12)
(12) ,
,  (13)
(13)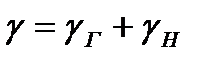 (14)
(14) (15)
(15) (16)
(16) (17)
(17) (18)
(18) (19)
(19) (20)
(20)
 (22)
(22) (23)
(23) (24)
(24) (25)
(25) (26)
(26) (27)
(27) (28)
(28) (29)
(29) (30)
(30) (31)
(31) , (32)
, (32) (33)
(33) (34)
(34) (35)
(35) (36)
(36) , (37)
, (37)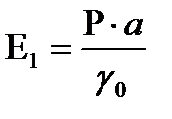 , (38)
, (38) ; (Н/м2, дин/см2), (39)
; (Н/м2, дин/см2), (39) (Н/м2, дин/см2), (40)
(Н/м2, дин/см2), (40) (пуаз, Па·с) (41)
(пуаз, Па·с) (41) – стационарлы ағуға әсер етуші кернеу.
– стационарлы ағуға әсер етуші кернеу. - dγ/dτ=f(Р) қисығынан көлбеудің Р координатасымен жанасқан мәнінен алынады.
- dγ/dτ=f(Р) қисығынан көлбеудің Р координатасымен жанасқан мәнінен алынады. ; сек (42)
; сек (42) (43)
(43)