|
|
Электролитпен коагуляциялау кинетикасы 8 главаТәжірибеден, сұйықтың тұтқырлық ағуының активтену энергиясы бірнеше ккал/моль екенін көреміз. Сұйықтықтардың тұтқырлықтарын анықтау. Сұйықтықтардың тұтқырлығын әр түрлі әдістермен анықтауға болады. Біз тек маңыздыларына тоқталайық. Құлап келе жатқан шар әдісі сұйықтыққа белгілі көлемі мен массасы бар шар еркін құлау жылдамдығын анықтауға негізделген. Сұйықтықтың турбулентті қозғалысы пайда болмас үшін шардың құлау жылдамдығы өте көп болмау керек, ал шар құлайтын ыдыс кең болу керек. Тұтқырлық коэффициентінің теңдеуінен шығатын теңдеуден оңай табуға болады:
Тәжірибеші шардың құлау жылдамдығы арқылы тұтқырлықты таба отырып, жүзгін бөлшектерінің радиустарын тұндыру жылдамдығы арқылы табуға тура келетін есепке кері келетін есепті шығарады. (2.7.) теңдеуінен шардың құлау жылдамдығы сұйықтықтың тұтқырлығына кері пропорционалды екені көрініп тұр. Мұндай тәуелділік шардың кең ыдысқа құламай, Гепплер вискозиметрінде сияқты сұйықтығы бар қисайған шыны түтікше бойынша қозғалғанда сақталады . Капилляр арқылы сұйықтықтың ағу әдісі радиусы және ұзындығы белгілі капилляр арқылы сұйықтықтың көлемінің ағып өту уақытына негізделген. Бұл жағдайда тұтқырлықты мына теңдеу арқылы есептейді:
мұнда V- τ уақытта ағып өткен сұйықтық көлемі; қалған белгілеулер (2.3.) теңдеуімен бірдей . Ротациялық вискозиметрлер арқылы анықтау. Тұтқырлықты бұл әдіс бойынша анықтайтын құрылғылар екі коаксиальді цилиндрден тұрады. Цилиндрлер арасындағы сақиналы тесіктерге зерттелетін сұйықтық құйылады. Цилиндрлердің бірін (әдетте ішкіні) айналдырады. Өте аз периодтан кейін цилиндрлердің ортасымен сұйықтықтың ағуының стационарлы режімі орнайды. Тұтқырлықты айналып тұрған цилиндрдің уақыт бірлігіндегі айналу санымен анықтайды. Осындай типтес құрылғылардың конструкциясын, бұрынғы Кеңес одағында М.П.Воларович жасаған. Ротациялық құрылғының басқа түрін Ф.Н.Шведов XIX- ғасырда жасаған болатын, ол да екі коаксиальді цилиндрлерден тұрады, оның сыртқысы тұрақты жылдамдықпен электрометр арқылы айналып тұрады, ал ішкісі жіңішке серпімді жіпке ілінген және оған орағытылу бұрышын санайтын көрсеткіш орнатылған. Сұйықтықты цилиндрлер ортасындағы кеңістікке құяды. Айналу кезінде сыртқы цилиндр сұйықтықты өзіне ілестіреді, ол ішкі цилиндрді айналуға келтіреді де, айналдыру күшінің моменті үйкеліс күштерінің моментіне тең болғанша белгілі бұрышқа айналдырады. Ішкі цилиндр ілінген жіп серпімді болғандықтан, бұл бұрыш тұтқырлыққа пропорциональды болады. Цилиндрдің айналу жылдамдығы мен айналу бұрышын байланыстыратын теңдеу бойынша, құрылғылардың тұрақтылықтарын біле отырып, тұтқырлықты есептеуге болады. Тәжірибеде абсолютті емес, есептен құрылғы тұрақтыларын алып тастауға болатын тұтқырлықты анықтаудың салыстырмалы әдістері жиі қолданылады. Бұл үшін шариктің құрау уақытын, ағу уақытын және т.б. параметрлерді стандартты ерітінділерге өлшеп алып, кейіннен осы шамаларды зерттелетін сұйықтықтарға өлшейді. Тұтқырлық мәні өлшенген параметрлерге пропорционалды болатындықтан, стандартты сұйықтықтардың тұтқырлығын біле отырып, алынған нәтижелерден зерттелетін сұйықтықтың тұтқырлығын есептейді. Тұтқырлық температураға күшті тәуелді болғандықтан, оны тек тұрақты температурада, құрылғыны термостатта қойып өлшеу керек . Коллоидтық жүйелердің тиімді тұтқырлығының ағу жылдамдығына тәуелділігі. Кірнелердің ағуының қарапайым жеке сұйықтықтардан немесе шын төменгі молекулалық қосылыстардан айырмашылығы, біріншілерде өлшенген күйде өлшемдері молекулалардың өлшемдерінен асатын коллоидтық бөлшектердің болуына байланысты. Мұндай бөлшектердің болуы ағып жатқан сұйықтықтың жеке молекулаларының жолын өзгертеді және жеке қабаттардың араласуына жағдай жасайды. Осының нәтижесінде дисперстік жүйелерде ерте турбуленттілік, яғни өлшенген бөлшектері жоқ сұйықтарға қарағанда төмен Рейнольдс сандары кезінде ламинарлы ағудың турбуленттіге ауысуы байқалады. Сонымен қатар, коллоидтық бөлшектер ағындағы сұйықтықтың кеңістігін тарылтады да, сұйықтық ағынына перпендикуллярлы бағытта орташа градиент жылдамдығын арттырады. Осының салдарынан кірненің тұтқырлығы дисперсиялық ортаның тұтқырлығынан жоғары болады. Көптеген кірнелердің ерекшеліктерінің бірі - ол Ньютон және Пуазейль теңдеулеріне бағынбауы. Қарапайым сұйықтықтар үшін уақыт бірлігінде капилляр арқылы өткен сұйықтық көлемі каппиллярдың соңындағы және басындағы р қысымдардың айырмашылығына тура пропорционалды. Дәл осындай қарапайым сұйықтықтар үшін ішкі цилиндрдің айналу бұрышы мен сыртқы цилиндрдің айналу жылдамдықтарының (Ф.Н.Шведов вискозиметрі тектес ротациялық құрылғыларда) арасында тура тәуелділік байқалады. Көптеген кірнелерде, майғындарда және үлкен молекулалық заттар ерітінділерінде мұндай тәуелділік жоқ, ал сәйкес келетін теңдеумен есептелген тұтқырлықтың айнымалы мәні бар және ол жылдамдық градиентінің функциясы болып келеді. Басқа сөзбен айтқанда, көптеген дисперстік жүйелердің тұтқырлығы жүйенің инвариантты сипаттамасы болмайды, ол анықталу жағдайларына, мысалы сұйықтықтың вискозиметрдегі ағу жылдамдығына, құрылғының типі мен өлшеміне тәуелді болады. Ньютон және Пуазейль заңдарына ұзартылған бөлшектері және деформациялануға қабілетті бөлшектері бар коллоидтық жүйелер, сонымен қатар, құрылымданған коллоидтық жүйелер бағынбайды. Созылыңқы, таяқша тәрізді бөлшектері бар коллоидтық жүйелердің тұтқырлықты ағуының аномалиясының себебі ағуға жағдай жасайтын ығысу кернеуінің өсуіне байланысты. Мұндай бөлшектер өздерінің ұзын осьтерімен ағын бағытында бағытталады, нәтижесінде гидродинамикалық кернеу азайып, сұйықтықтың қозғалысы тездетіледі. Созылыңқы бөлшектердің ағын бағытында бағытталуын жылдамдықтың өсетін градиентінде кірнелерде сәуленің қосарлана сыныун өлшеу арқылы оңай түсіндіруге болады. Деформацияланатын бөлшектері бар жүйелер, мысалы майғындарда да осындай тәуелділік байқалады. Берілетін ығыстыру кернеуінің өсуі және ағу жылдамдықтарының өсуімен капиллярлы фазаның тамшылары ұзарады, шарлардан эллипсоидтарға айналады да ағуды оңайлатады және тұтқырлықты төмендетеді. Осындай жағдайлар иілгіш жұмырланған макромолекулалары бар жоғары молекулалы қосылыстардың ерітінділері аққанда да байқалады. Мұнда тұтқырлықтың азаюы молекулалардың жазылуы мен ағын бағытына қарай бағытталуына байланысты. Әрине, барлық айтылған жағдайларда байқалатын немесе тиімді тұтқырлық туралы айтылған, себебі сұйықтықтың шын тұтқырлығы ағу жылдамдығына тәуелсіз. Ньютон және Пуазейль заңдарына құрылымданған сұйықтықтар да бағынбайды. Үлкен практикалық маңызы мен бірқатар принципиалды ерекшеліктеріне байланысты құрылымданған сұйықтықтардың тұтқырлығын бөлек қарастырған жөн. Қорытындылайтын болсақ, Ньютон заңына бағынатын сұйықтықтарды нормалды, ал Ньютон заңына бағынбайтын жүйелердіаномальді сұйықтықтардеп атайды. Капиллярлы вискозиметрмен жұмыс істегенде зерттелетін сұйықтық аномальді немесе нормальді екенін анықтайтын қарапайым әдіс бар. Ол үшін сұйықтық ағып бітетін артық қысымды р белгілі сұйықтық көлемінің ағып өтетін уақытына көбейтеміз. Пуазейль теңдеуін былай көрсетуге болады:
бұдан рτ өрнегі ағуды болдырған қысымға тәуелсіз болса, онда сұйықтық нормальді, ал егер тәуелді болса, онда аномальді болады. Ротациялық вискозиметрмен жұмыс істегенде мұндай көрсеткіш ретінде цилиндрдің айналуын қамтамасыз етіп тұрған салмақ шамасына уақыт бірлігіндегі цилиндрдің айналымдарының санының тәуелсіздігін келтіруге болады . 2.3 Құрылымдық тұтқырлық Жоғарыда көрсетілгендей, құрылымданған жүйелер Ньютон заңына бағынбайды. Бұл сұйықтықта бір-бірімен байланыссыз құрылымдар үзінділерінің болуымен, немесе жүйеге салыстырмалы аз күш әсер еткеннен бұзыла алатын азберіктікті тұтас құрылымдық тордың болуымен сипатталады. Бірінші жағдайда жүйе ағу кезінде сұйықтық секілді болады, онда бағыттала немесе деформациялана алатын жүзгін бөлшектер бар. Құрылымдық тордың үзінділері ағыстағы қабаттардың әр-түрлі жылдамдықтарының нәтижесінде бұзылады, ал бұзылған тордың жеке элементтері, егерде созылыңқы пішінді болса, өзінің ұзын осі бойынша ағыс бағытында бағытталады. Екінші жағдай қиындау. Басында Ф.Н. Шведов, сонан соң Бингам құрылымның бұзылуына керекті белгілі ѳ дағдарыстық мәнінен ығысудың р кернеуі асатын болса, яғни р – ѳ >0 шарты орындала бастағанда ғана беріктігі аз кеңістіктік құрылымды жүйенің ағуы басталады деп ойлады. Мұндай ағысты Бингам пластикалық, ал ѳ ығысудың дағдарыстық кернеуін аққыштықтың шегідеп атады . Пластикалық ағысы бар жүйелер үшін Ньютон теңдеуі Бингам теңдеуімен ауыстырылуы керек: P- ѳ =η1 (du/dx) Немесе : P =η1 (du/dx)+ ѳ (2.9.) мұнда η1 - жүйенің пластикалық ағысына сәйкес келетін тұтқырлық (пластикалық тұтқырлық). Құрылымдық тор болмағанда ѳ мәні нольге теңесіп, Бингам теңдеуі Ньютон теңдеуіне ал пластикалық тұтқырлық η1 сұйықтықтың шын тұтқырлығына айналады. Бингамның ойынша, р ѳ - ден асқан уақытта жүйенің тұтқырлығы бірден тұрақты мәнге ие болады. Мұндай жағдайда du/dx- р- мен тәуелділігі түзу сызықты болады (2.5. сурет).
ѳ p ѳ f ѳ B ѳ макс p
Суретке сәйкес пластикалық тұтқырлықты былай өрнектеуге болады:
мұнда Бингам теңдеуіне бағынатын жүйелердің мысалына саз қойыртпақтары және консистенттік жаққыштарды келтіруге болады. Алайда көптеген құрылымданған коллоидтық жүйелер үшін du/dx- р- мен тәуелділігі түзу сызықпен емес, қисықпен өрнектеледі (2.6.-сурет). Мұндай құбылыстың себебі аққыштықтың шегіне жеткенде құрылым бірден емес, ақырындап сұйықтықтың қозғалыс жылдамдығының градиентінің өсуіне байланысты бұзылады. Соған қарағанда, ығыстырудың үш дағдарыстық кернеуін ажыратуға болады: 1) θ Коллоидтық жүйелердің құрылымдық тұтқырлығын П.А. Ребиндер және оның мектебі, сонымен қатар А.А. Трапезников қызметкерлерімен бірге зерттеген. Бұл жұмыстардың нәтижесінде ағудың әртүрлі жылдамдығында коагуляциялық құрылымда бір-біріне қарама-қарсы екі үдеріс - бұзылу және қайта қалпына келтіру жүретіні анықталды. Бұл тұрақталған ағыстағы үдерістер арасындағы тепе-теңдік күйді тиімділік тұтқырлығы сипаттайды. Жүйенің өте аз жылдамдықтарында мардымсыз бұзылулар болады, себебі ағыспен айырылмастай байланысқан бұзылулар ағу үдерісінің баяулығына байланысты тиксотропты қайтадан қалпына келіп үлгереді де, жүйенің ағуын құрылымның бұзылуынсыз жүреді деп айтуға болады, яғни сырғу құбылысы байқалады. Ағудың үлкен жылдамдықтарында жүйенің құрылымы айтарлықтай бұзылады, бұл уақытта бұзылған құрылым үдеріст ің тездігіне байланысты мардымсыз ғана қайта қалпына келеді. Құрылымданған сұйықтықтар мен пластикалық денелердің ағуын сипаттау үшін пластикалық емес, жүйедегі ығысу кернеуінің өсуімен азаятын η
Құрылымданған коллоидтық жүйелер тұтқырлығы оны анықтау жағдайларына, соның ішінде ол өлшенген кездегі жылдамдық градиентіне тәуелді. Сондықтан мұндай жүйелердің тұтқырлықтарының мәндерін олар тек Рейнольдс санының бірдей мәндерімен сипатталатын күйлерде ғана табылғанда салыстыруға болады. Сондай–ақ кірнелердің де тұтқырлықтарын ығыстырудың бір ғана мәнінде анықтамай р мәнінің жеткілікті үлкен аралығында жүйенің реологиялық қасиеттерін сипаттайтын du/dx, р қисықтарын алу керек. Алайда бір ғана вискозиметрді қолданып, бірдей жағдайларда өлшегенде жүйенің қашан дайындалғандығына, оның алғы тарихына байланысты қандайда белгілі жүйе үшін табылған тұтқырлықтың мәндері айтарлықтай өзгереді. Мысалы, коллоидтық жүйенің ұзақ уақыт тұрғанында оның тұтқырлығы құрылымдану процесіне байланысты біртіндеп өседі. Мұндай тұтқырлықтың өзгерістерін темір тотығының гидраты немесе ванадийдің бес тотықты зольдері үшін байқауға болады. Бір жағынан, механикалық әсердің нәтижесінде, мысалы жүйенің капилляр арқылы өтуі кезінде жүйеде түзілген құрылымдар бұзылуы мүмкін, соның салдарынан тұтқырлығы азаяды. Тікелей бірінен кейін бірі капиллярлы вискозиметрдің көмегімен тұтқырлықтарды өлшеу кезінде белгілі шекке ұмтылатын, үздіксіз азаятын мәндердің алынуы осымен түсіндіріледі.
2.4 Шын серпімділікті көрсететін коллоидтық жүйелердің механикалық қасиеттері. Алдыңғы бөлімде коллоидтық жүйелердің құрылымды-механикалық ерекшеліктерін қарастырғанда біз бұл жүйелерді сұйықтықтар деп есептедік. Алайда коллоидтық жүйелердің бірқатар қасиеттерін, егерде оларды қатты дене деп қарастырсақ, түсіндіруге болады. Соңғы жағдай серпімділіктің немесе эластикалықтың белгілі дәрежесі бар және аққыштықтың шын шегімен сипатталатын (серпімділік шегі) яғни ағу тіпті байқалмайтын ығысу кернеуінің шегі болатын коллоидтық жүйелерді зерттегенде үйлесімді. Әдетте мұндай қасиеттер жеткілікті концентрленген қатты тәріздес сірнелер және конденсациялы-кристалданған құрылымы бар жүйелерге тән. Алайда серпімді сірнелердің механикалық қасиеттерін қарастырмастан бұрын, ығысу модулі және кернеудің релаксациялық периоды секілді жүйелердің қасиеттерінің сипаттамаларына тоқталайық. Ығысу модулі Е әрбір дененің қаттылығын және оның пішінін сақтау қабілеттерін сипаттайды. Бұл шаманы белгілі Гук теңдеуінен шығарып алуға болады: ε=Р/Е (2.11) мұнда ε-шын қатты денелердегі ығысудың салыстырмалы деформациясы; Р- ығысу кернеуі. Бұл теңдеу тек аз деформациялар үшін әділетті, себебі серпімділік шегі деп аталатын, белгілі дағдарыстық кернеу кезінде дене өзінің серпімді қасиеттерін жоғалтады және қалдық деформацияларды сақтап қалады. Е ығысу модулі жүктеме берудің бірдей жылдамдықтары кезінде дененің табиғатына және температурасына тәуелді. Қатты денелер үшін Е шамасы өте үлкен мәндерге, ал шын сұйықтықтарда Е=0 жетеді, себебі алға ұмтылудың қандай болмасын аз шамасы сұйықтықтың ағуына әкеледі. Төменде бірқатар заттар үшін Е ығысу модулі мәндерінің (кгс\см2) мысалдары келтірілген: желатина 0,5 % ерітіндісі 4*10-10 10 % ерітіндісі (тоңазытпа) 5*10-12 каучук 1,7*102 қорғасын 4,8*104 тал (емен) 8*104 болат 8*105 А.А. Трапезников жүйенің сипаттамалы реологиялық параметрі деформацияның жоғары жылдамдықтарында тез релаксацияланатын жүйелерде ығысу шекті қайтымды деформациясы εмакс болатынын көрсетті. Әртүрлі коллоидтық жүйелерде ол әрқалай болуы мүмкін. Мысалы, қойыртпақтарда ол бірнеше немесе бірнеше ондаған пайыз, ал эластикалық сірнелерде және полимерлердің бірқатар ерітінділерінде он мыңдаған пайыздар болуы мүмкін. Мұндай мәндер каучуктердің ығысу шекті қайтымды деформацияларының әдеттегі шамаларынан өте көп. Релаксация периоды (немесе уақыты) материалдық жүйенің молекулалары немесе басқа құрылымдық элементтерінің бірқатар қозғалғыштығының барлығына жіне бір-біріне қатысты орналасу қабілетіне байланысты. Осының нәтижесінде денеде оның деформациялануынан туған кернеу уақыт өткеннен кейін белгілі дәрежеде "сорылады " алады. Мұндай уақыт аралығында кернеудің азаю үдерісін релаксация деп атайды. Релаксация жылулық қозғалыстың нәтижесі және оның жалпы сипатты балады. Релаксациялана алатын жүйелердің деформациясын суреттейтін бірқатар теңдеулер берілген. Ең қарапайымы Максвелл теңдеуі, ол серпімді-тұтқыр дене теориясынан шығады: DP/dτ=E(dε/dτ)-(P/τ*) (2.12) мұнда τ* - релаксация периоды немесе уақыты деп аталатын тұрақты. Тұрақты температурада Максвелл теңдеуі релаксацияның негізгі сапалық заңдылықтарын береді. Егер дененің деформациясын тұрақты етіп ұстаса (ε=0), онда dε/dτ=0, сонда Максвелл теңдеуінен Р кернеу уақыт бойынша мына заңмен өзгереді: (dP/dτ)+(P/τ*)=0 (2.13) бұл теңдеуді интегралдап, мынаны аламыз: Р=Р0 е-τ/τ* (2.14) Бұдан уақыт өткен сайын деформацияланған денедегі кернеу экспоненциалды заң бойынша азаятының, ал релаксациялау жылдамдығын сипаттайтын τ* тұрақты, дененің бастапқы кернеуі, деформация тұрақты болғанда, е=2,72 есе азаятын (натурал логарифмнің негізі) уақыт аралығына тең екенін байқаймыз. Төмен тұтқырлықты сұйықтықтардың кернеуінің релаксациялық периоды молекулалардың көп қозғалғыштығының нәтижесінде өте аз болады. Тұтқырлықтың көбеюімен сұйықтықтардың релаксация периоды артып, қатты денелердің кернеуінің релаксация уақытына жақындайды. Кристалдар үшін релаксация процесі өте баяу жүреді. Төменде мысал ретінде бірқатар заттардың кернеуінің релаксация периодының мәндері τ* (с) берілген: Су 3*10-6 Үпілмәлік майы 2*10-3 Копал лагы 2*10 Канифоль (55˚С) 5*10 Желатин , 0,5 % еріт. 8*102 Канифоль (12˚С) 4*106 Идеал қатты заттар ∞ Желатинаның өте сұйылтылған 0,5% сулы ерітіндісінің салыстырмалы үлкен релаксация периоды назар аудартады. Бұл ерітіндінің релаксация периоды сұйықтықтардың кернеуінің релаксация периодына қарағанда қатты денелердің кернеуінің релаксация периодына жақын. Бұл желатина ерітіндісінде қайта топтасу үшін салыстырмалы көп уақыт керек ететін салыстырмалы үлкен құрылымдық элементтердің (желатина макромолекулалары) болуымен түсіндіріледі. |
|
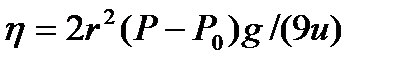 (2.7)
(2.7)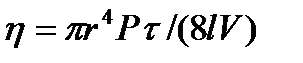 (2.8.)
(2.8.)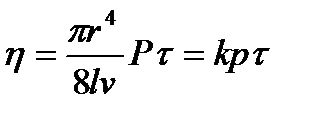

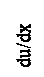
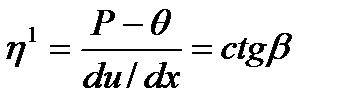 (2.10.)
(2.10.)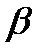 - абцисса осімен түзудің арасындағы бұрыш.
- абцисса осімен түзудің арасындағы бұрыш. - бірінші немесе минималды аққыштық шегі, ол ағудың басталуына сәйкес келеді (құрылымның бұзылуының басына); 2) θв- Бингам бойынша аққыштық шегі, ол қисықтың тік сызықты аумағын жалғастырғанда абцисса осін қиып өткендегі кесіндіге сәйкес келеді; 3) θ
- бірінші немесе минималды аққыштық шегі, ол ағудың басталуына сәйкес келеді (құрылымның бұзылуының басына); 2) θв- Бингам бойынша аққыштық шегі, ол қисықтың тік сызықты аумағын жалғастырғанда абцисса осін қиып өткендегі кесіндіге сәйкес келеді; 3) θ  - аққыштықтың максималды шегі, ол қисық түзу сызыққа айналатын р мәніне сәйкес келеді. Соған қарағанда, θ
- аққыштықтың максималды шегі, ол қисық түзу сызыққа айналатын р мәніне сәйкес келеді. Соған қарағанда, θ 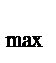 - сұйықтықтағы құрылым толығымен жойылатын кернеу болып келеді. Барлық үш шек те жүйеде кездесетін құрылымдардың механикалық қасиеттерін сипаттайды.
- сұйықтықтағы құрылым толығымен жойылатын кернеу болып келеді. Барлық үш шек те жүйеде кездесетін құрылымдардың механикалық қасиеттерін сипаттайды. тиімді тұтқырлықты пайдалану керек.
тиімді тұтқырлықты пайдалану керек. 2.7 – сурет.
2.7 – сурет.