|
|
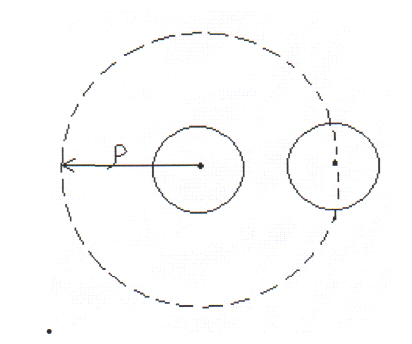
Электролитпен коагуляциялау кинетикасы 21 главаУльтрасүзу. Ультрасүзу ол қысым арқылы жүретін диализ. Шын мәнінде ультрасүзуді зольдерді тазалау емес концентрлеу әдісі деп қарастыруға болады. Кеуектілігі әртүрлі ультрасүзгілерді пайдалана отырып ультрасүзуді дисперстік жүйелерді әртүрлі монодисперстік фракцияларға бөлуге болады. Алайда әрбір жарғақтың кеуектілігі кең аралықта өзгеретін болғандықтан толық монодисперстік жүйені алу өте қиын. Ультрасүзу үшін көптеген құралдар ұсынылуда. Ультрасүзу әрқашанда қысым астында жүргізілетіндіктен барлық құралдарда да жарғақ иә үсақ тесіктері бар пластинкаға жабылады, иә тікелей глазурленбеген фарфор ыдыстарының қабырғаларында алынады. Мысалы, белгілі Бехгольд ультрасүзгілерін кеуек фарфор ыдысының қабырғасына сұйытылған каллодийді жағып, содан соң оны кептіру арқылы алады. Коагуляция кинетикасы Лиокірнелердің түрақтылығы мен коагуляциясын қарастырмай түрып, алдымен коагуляция кинетикасының теориясына тоқталайық, өйткені ол коллоидтық жүйелердің түрақтылығының теорияларынан бүрын жасалған. Коагуляцияны (айқын коагуляцияны) баяу немесе жылдам коагуляция деп екіге бөліп қарастырады. Жылдам коагуляция деп броундық қозғалыстағы бөлшектердің жақындауы олардың бірігуімен аяқталатын коагуляцияны айтады. Баяу коагуляцияда коллоидтық бөлшектердің бетінде ішінара қос электрлік қабат, сольваттық қабат және с.с. сақталатындықтан бөлшектердің бірігуі тек ерекше соқтығысулардың нәтижесінде ғана болады. Сонымен екі терминнің де шартты түрде қабылданғаны көрініп түр. Жылдам коагуляция кинетикасының теориясын польшалық ғалым Смолуховский жасады. Ол кірнелердің бөлшектерінің арасында тартылу және тебілу күштері әсер ететінін, тебілу күштерінін электролит енгізгенде әлсіреп, электролиттің концентрация жылдам коагуляцияны болдыруға жеткенде тебілу күшінің жоғалатынын айтты. Осындай астабилизицияланған (тұрақсызданған) кірненің бөлшектері броундық қозғалыстың нәтижесінде бір-біріне жақындағанда молекулалық тартылу күшінің әсерінен бірігіп, агрегат түзеді, әрі қарай олар осы біріккен күйінде броундық қозғалыс жасайды. Бөлшектердің арасындағы әсер ететін күштің табиғатын Смолуховский қарастырған жоқ. Өзінің теориясын жасағанда Смолуховский жылдам коагуляцияның жылдамдығы кірненің сандық концентрациясына ν, броундық қозғалыстың қарқындылығына (ол диффузия коэффициентімен D анықталады) екі бөлшек бірігу үшін олардың кризистік арақашықтығына ρ байланысты деп қарастырды. ρ қашықтығы коллоидтық бөлшектің диаметрінен көбірек те болуы мүмкін (1.7-суретті қара)
1.7 - сурет. Жылдам коагуляциядағы бөлшектердің әсер ету сферасы. Сонымен, егер радиусы ρ сфераны қарастырсақ, оның орталығы бөлшектердің біреуінің орталығымен сәйкес келсін. Екінші бөлшек бірінші бөлшекпен оның орталығы осы сферамен жанасатын жағдайда ғана бірігеді. Бұл сфераны ол жұтылу сферасы деп атады. ρ -дан көбірек қашықтықтағы молекулалық күштердің броундық қозғалысқа әсерін және бөлшектердің бірігуін Смолуховский болмайды деп қарастырды. Смолуховский бойынша жылдам коагуляция кезінде жеке бөлшектер өзара соқтығысып қосарланған бөлшектер, содан соң қосарланған бөлшектер жеке бөлшектермен соқтығысып үштік бөлшектер және сол сияқты болып кете береді. Күрделі бөлшектердің де өзара соқтығысуы мүмкін. Бірақ үш немесе одан да көп және немесе күрделі бөлшектердің соқтығысу ықтималдығы аз болғандықтан оларды есепке алған жоқ. ν1 ; ν2 ; ν3 … деп бастапқы бөлшектердің біреуінен, екеуінен, үшеуінен және с.с. тұратын бөлшектердің сандық концентрациясын белгілеп, бастапқы τ =0 уақытында: ν1 = ν0 және ν2 = ν3 =… νn = 0 деп жазуға болады. Ал τ уақыт өткеннен кейін: ν = ντ = ν 1+ ν 2+ ν3+…. болады . Мұндағы ν соңғы сандық концентрация. Әрине мынадай теңсіздіктің орындалуы сақталады: ν < ν0 Коагуляция процесін Смолуховский екінші реттілік реакция сияқты етіп қарастырды. Сонда коагуляция жылдамдығы бөлшектердің ρ қашықтыққа жақындау ыктималдығын (немесе жиілігін) анықтайтын сондай концентрациясының квадратына тура пропорционалды болады: - мұндағы k жақындау ықтималдығын сипаттайтын константа. Теңдеудің алдындағы (-) таңбасы τ уақыт өткен сайын сандық концентрацияның v азаятынын көрсетеді. Смолуховский бойынша: k=4π·Д·ρ Теңдеуді былайша көрсетуге болды: - және (2)теңдеуді v0 деп v дейін және 0-ден τ -ға дейін интегралдап, келесі теңдеуді аламыз:1/v-1/ v0=k τ (3) Бұдан τ уақытында зольдің сандық концентрациясы мынаған тең:
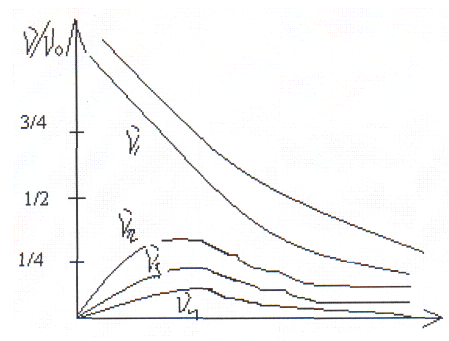
Жартылай коагуляциялану уақытын (θ) енгізе отырып, мынаны жазуға болады: К v0=1/θ (5) Сонда (4)теңдеуді былайша көрсетуге болады: (6)теңдеуден τ –дың әртүрлі мәндері үшін θ және к-ны есептеуге болады. Бірлік көлемдегі зольде, τ/θ шамасынабайланысты бөлшектердің жалпы санының салыстырмалы өзгеруі ∑v және әртүрлі бөлшектердің сандарының v1, v2, v3…. өзгеруі 1.8 суретте көрсетілген
τ/θ Сурет. (6)-теңдеуден 1/ ν уақытқа τбайланысты сызықты функция болатыны көрініп түр. Тәжірибе арқылы шындығында да солай болатыны бірнеше рет дәлелденді. Смолуховский теориясы бойынша ρ-ны есептеуге болады. (5) -теңдеуді былайша жазуға болады:
Эйнштейн теңдеуі бойынша:
Мұндағы: к - Больцман константасы; η-дисперсиялық ортаның динамикалық тұтқырлығы; r - бөлшектердің радиусы. Соңғы теңдеуден:
немесе
Эксперимент бойынша: Смолуховский өзінің теориясын жасағанда монодисперстік кірнелерді карастырды. Мюллер дәл осындай теорияны полидисперстік жүйелердің коагуляция үшін жасады. Ол әртүрлі өлшемдегі бөлшектер, бірдей бөлшектерге қарағанда жылдамырақ агрегацияланатынын көрсетті. Ол кезде үлкен бөлшектер коагуляция "туынтектерінің" рөлін атқарды. Мюллердің теориясы коагуляцияның автокаталитикалық сипатын, яғни коагуляция оның жылдамдығының уақытқа байланысты өсетіндігін түсіндірді. Мюллер, сондай-ақ, бөлшектердің пішіні үзындау болғанда ілгерілемелі броундық қозғалысқа айналу қозғалыс қосылып, сондықтан бөлшектердің соқтығысу ықтималдығының артатынын көрсетті. Бұл теория жылдам коагуляция үшін жасалғандықтан, баяу коагуляция үшін Смолуховский әлі толық астабилизацияланбаған (түрақсызданбаған) бөлшектер үшін, олардың жақындасу тиімділігін ξ еске алатын түзетпе енгізуді ұсынды.
Электролитпен коагуляциялау кинетикасы Коагуляцияның сипаттамасы ретінде Зигмонди Коагуляция жылдамдығын пайдалануды ұсынған болатын. Коагуляция жылдамдығы
Теңдіктен кейінгі “ Коагуляция дәрежесі деп бірлік уақытта бөлшектердің соқтығысуының жалпы санын z бірлік уақыттағы тиімді соқтығысулар санына Zm қатынасын айтады. Егер Егер Егер Бөлшектер соқтығысқанда серпімді шарлар сияқты жан-жаққа шашырап кетпей, потенциалдық тосқауылдан асу керек. Ендеше, коллоидтық бөлшектердің кинетикалық энергиясы осы асудан асатындай болғанда ғана коагуляция болады. Коагуляция дәрежесін арттыру үшін потенциалдық асуды төмендету керек. Оған кірнеге электролит- коагулянт қосу арқылы қол жеткізуге болады. Коагуляция жылдамдығының электролит концентрациясына тәуелдігі 1.1- суретте көрсетілген.
1.1- сурет. Коагуляция жылдамдығының электролит концентрациясына тәуелділігі. Суреттегі үш аймақты жеке қарастыруға болады: 1. 2.
3.
Жылдам коагуляция Жылдам коагуляцияның кинетикалық теориясын М.Смолуховский 1916 жылы келесі тұжырымдамаға сүйене отырып жасады: 1. Қарастыратын жүйені монмдисперстік етіп алды, яғни бөлшектердің радиустары r бірдей болады. 2. Бөлшектердің соқтығысуының барлығын тиімді (пәрменді) деп қарастырады, яғни 3. Тек біріншілікті бөлшектердің соқтығысулары ғана қарастырылады. 4. Коагуляция кинетикасын бимолекулалық реакциясының кинетикасына ұқсас деп қарастырады:
Бұл теңдеуді интегралдап, айнымалы шамаларға бөлсек:
Мұндағы: Жылдам коагуляцияны сипаттау үшін коагуляция периоды (жартылай коагуляция периоды)
Жылдам коагуляция теориясына сәйкес коагуляция константасы диффузия коэффицентінетәуелді болады және оны мына теңдеумен есептеуге болады: K=16*r* Бұл теңдеуге диффузия коэффицентінің мәнін қоятын болсақ, мынадай теңдеу аламыз: K= Сонымен, ортаның тұтқырлығы және температурасын біле отырып, жылдам коагуляция жылдамдығының константасын есептеуге болады екен. Смолуховский теориясы эксперимент арқылы бірнеше рет тексеріп, оның дұрыстығы дәлелденді. Баяу коагуляция Баяу коагуляция энергетикалық тосқауыл болғандықтан, соқтығысулардың толық тиімді (пәрменді) болмайтындығымен байланысты. Смолуховский теориясының формуласына коагуляция дәрежесі 2 шамасын енгізу теория мен тәжірибенің бір-біріне сәйкес келмейтіндігін көрсетті. Сондықтан баяу коагуляцияның жетілген теориясын Н.Фукс жасады. Ол коагуляцияның кинетикалық теңдеуіне коагуляциялық энергия тосқауылын Р- стерикалық фактор, К- Больцман тұрақтысы Сонымен баяу коагуляцияның жылдамдық константасын есептеу үшін коагуляцияның потенциалдық тосқауылын білу керек екен. Оның шамасы ең алдымен 2.Дисперстік жүйелердің тұрақтылығының түрлері Дисперстік дүйелердің тұрақтылық мәселесі коллоидтық химияның маңызды мәселелерінің бірі. 1917 жылы Песков дисперстік жүйелердің тұрақтылығын қарастырғанда 2 түрлі тұрақтылыққа мән беру керек екенін айтты. Олар: седиментациялық немесе кинетикалық тұрақтылық және агрегаттық тұрақтылық. Тұрақтылықтың бұл 2 түрі механизмдері бойынша бір бірінен өзгеше болады. Сондықтан оларды жеке жеке қарастырайық.
Дисперстік жүйелердің седиментациялық тұрақтылығы Седиментациялық тұрақтылық деп дисперстік жүйелердің уақыт бойынша жүйенің көлемінде бөлшектердің таралуын өзгеріссіз сақтап қалу, яғни жүйенің ауырлық күшке қарсы тұру қабілетін айтады. Архимед заңы бойынша массаның орнына тиімділік массасын қоямыз, сонда бөлшек шөгуіне әсер ететін иауырлық күші мынадай болады: Fсед = m1g = V(ρ-ρ0)g (1.2) Тиімділік массасы m1 = V(ρ-ρ0) (1.3) болғандықтан бөлшектің иә шөгуі мүмкін ( егер Бөлшектер шөккенде дисперстеуші ортаның үйкеліс күші (Ғүй.) оларға қарсы әсер етеді: Ғүй.= В*Uсед. (1.4) Мұндағы : Uсед.- бөлшектің шөгу жылдамдығы ( седиментациялық жылдамдық); В- үйкеліс коэффициенті. Сонымен, седиментациялық күштің әсерінен бөлшек бірқалыпты үдей қозғалады да, оны азайтатын үйкеліс күші де оған сәйкес артады. Нәтижесінде, седиментацияның стационарлық режимі орнығып, ол кезде Ғсед.=Ғүй., бөлшек тұрақты жылдамдықпен шөгеді. Сонымен, V(ρ-ρ0)g= В*Uсед.. Бұдан седиментациялық жылдамдықты табатын болсақ: Uсед.= Седиментация үдерісін сипаттау үшін әдетте седиментация жылдамдығы Uсед. емес, седиментацияның меншікті ағынын ісед. пайдаланылады. Седиментацияның меншікті ағыны деп бірлік уақытта седиментация бағытын қиятын бірлік аудан қимасынан шөккен бөлшектер санын айтады. Оның өлшем бірлігі: [ісед.]= бөлшек/см2*с; Ендеше: ісед.= Uсед.* ісед.= Сонымен, седиментацияның меншікті ағыны V, Бұдан шар тәрізді бөлшектер үшін седиментациялық меншікті ағын радиустың квадратына тура, ал ортаның тығыздығына кері пропорционал екенін байқаймыз. Алайда, седиментация үдерісін қарастырғанда біз осы уақытқа дейін броундық қозғалысты еске алған жоқпыз. Микроскопиялық және коллоидтық өлшемдегі бөлшщектер броундық қозғалыста болатыны белгілі. Броундық қозғалыстың салдарынан диффузия болады, ол бөлшектердің концентрациясын төменгі қабаттарда артуына әкеп соғады. Сонымен, екі қарама- қарсы ағын байқалады: седиментация ағыны ісед. және диффузия ағыны ідиф.. Диффузия ағынын былай көрсетуге болады:
Бұл ағындардың бәсекелестігінің нәтижесі қалай болады? 3 түрлі жағдайда қарастыруға болады: 1) Бұл теңсіздік орындалу үшін Т және 2) Бұл жағдай Т және 3) |
|
 v/
v/  τ=k·v2 (1)
τ=k·v2 (1) (4)
(4) (6)
(6)
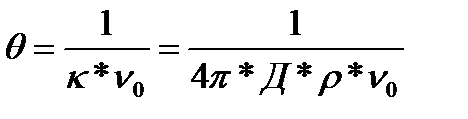
 (7)
(7)
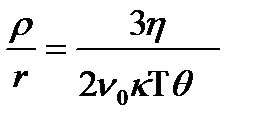 (8)
(8) ендеше
ендеше  қашықтығы 2r -ге өте жақын екен. Осындай қашықтықта ғана бөлшектердің тартылу күші әсер етіп, олардың молекулалық тартылуының энергиясы, броундық қозғалыстың жылулық қозғалысының энергиясынан, ендеше броундық қозғалыстан ρ/2кТ көп болады.
қашықтығы 2r -ге өте жақын екен. Осындай қашықтықта ғана бөлшектердің тартылу күші әсер етіп, олардың молекулалық тартылуының энергиясы, броундық қозғалыстың жылулық қозғалысының энергиясынан, ендеше броундық қозғалыстан ρ/2кТ көп болады. (9)
(9) деп- бірлік уақытта жүйенің тұрақты көлемінде коллоидтық бөлшектердің концентрациясының өзгеруін айтады.
деп- бірлік уақытта жүйенің тұрақты көлемінде коллоидтық бөлшектердің концентрациясының өзгеруін айтады. . Мұндағы
. Мұндағы  - бөлшектердің концентрациясы,
- бөлшектердің концентрациясы,  - уақыт.
- уақыт. ” таңбасы бөлшектердің концентрациясы уақыт бойынша азаятынын, ал коагуляция жылдамдығы әрқашанда оң болатынын көрсетеді.
” таңбасы бөлшектердің концентрациясы уақыт бойынша азаятынын, ал коагуляция жылдамдығы әрқашанда оң болатынын көрсетеді.
 болса, онда коагуляция болмайды, коллоидты ерітінді агрегаттық тұрақты болады.
болса, онда коагуляция болмайды, коллоидты ерітінді агрегаттық тұрақты болады. болса, онда жүйелі коагуляция болады, яғни бөлшектердің әрбір соқтығысуы олардың бірігуіне әкеп соғады.
болса, онда жүйелі коагуляция болады, яғни бөлшектердің әрбір соқтығысуы олардың бірігуіне әкеп соғады. болса, онда баяу коагуляция байқалады, яғни бөлшектердің соқтығысуларынан кейбіреулері ғана олардың бірігуіне әкеп соғады.
болса, онда баяу коагуляция байқалады, яғни бөлшектердің соқтығысуларынан кейбіреулері ғана олардың бірігуіне әкеп соғады.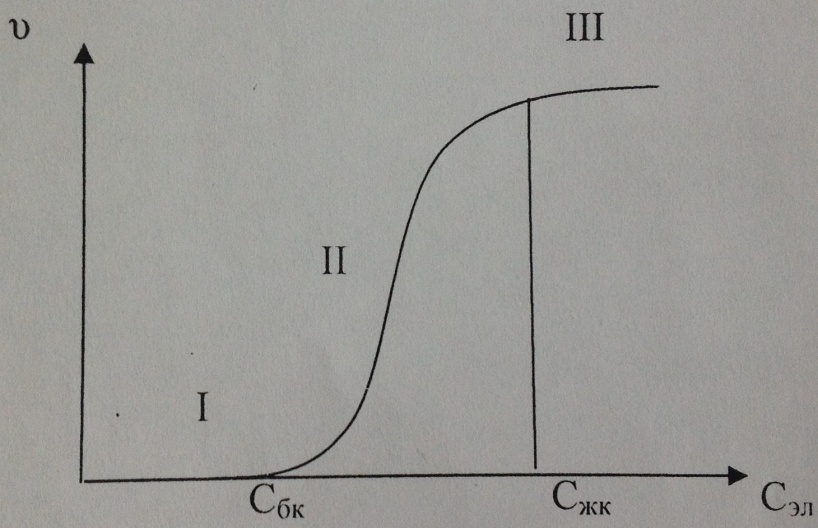
 . Ендеше кинетикалық энергия
. Ендеше кинетикалық энергия  (мұндағы к- Больцман тұрақтысы) болғандықтан лиофобтық кірне агрегаттық тұрақты болады.
(мұндағы к- Больцман тұрақтысы) болғандықтан лиофобтық кірне агрегаттық тұрақты болады.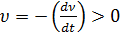 ;
;  , яғни коагуляцияның потенциалдық асуы (тосқауылы) көп шама, бірақ коллоидтық бөлшектердің кинетикалық энергиясымен шамалас және электролит- коагулянт концентрациясы артқан сайын ол азаяды да, ал коагуляция жылдамдығы өседі. Сбк- баяу коагуляцияның табалдырығы, Сжк- жылдам коагуляцияның табалдырығы. Қисықтық бұл аймағы мынадай тәуелділікті өрнектейді:
, яғни коагуляцияның потенциалдық асуы (тосқауылы) көп шама, бірақ коллоидтық бөлшектердің кинетикалық энергиясымен шамалас және электролит- коагулянт концентрациясы артқан сайын ол азаяды да, ал коагуляция жылдамдығы өседі. Сбк- баяу коагуляцияның табалдырығы, Сжк- жылдам коагуляцияның табалдырығы. Қисықтық бұл аймағы мынадай тәуелділікті өрнектейді:
 . Бұл аймақта бөлшектердің бір-біріне соқтығысуы олардың біріуіне әкеп соғады, яғни, жылдам коагуляция жүреді.
. Бұл аймақта бөлшектердің бір-біріне соқтығысуы олардың біріуіне әкеп соғады, яғни, жылдам коагуляция жүреді.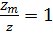
 ; мұндағы К- коагуляция жылдамдығының константасы.
; мұндағы К- коагуляция жылдамдығының константасы.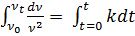
 (1.9)
(1.9) - уақыт t=0 кезіндегі кірне бөлшектерінің концентрациясы;
- уақыт t=0 кезіндегі кірне бөлшектерінің концентрациясы;  уақытындағы кірне бөлшектерінің концентрациясы.
уақытындағы кірне бөлшектерінің концентрациясы.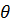 пайдаланылады. Коагуляция периоды
пайдаланылады. Коагуляция периоды  болғанда
болғанда  (1.10)
(1.10) *D (1.11)
*D (1.11) (1.12)
(1.12) еске алатын көбейтіндісін енгізді:
еске алатын көбейтіндісін енгізді:  (1.13)
(1.13) Na- Авогадро саны.
Na- Авогадро саны. потенциалына тәуелді болады.
потенциалына тәуелді болады. - дисперстік фаза бөлшектерінің тығыздығын;
- дисперстік фаза бөлшектерінің тығыздығын;  - дисперстеуші ортаның тығыздығын;
- дисперстеуші ортаның тығыздығын;  - дисперстеуші ортаның тұтқырлығын; V-бөлшектің көлемін білу керек.
- дисперстеуші ортаның тұтқырлығын; V-бөлшектің көлемін білу керек. болса), иә бетке қалқап шығуы мүмкін ( егер
болса), иә бетке қалқап шығуы мүмкін ( егер  болса).
болса). (1.5)
(1.5) ; мұндағы
; мұндағы  (1.6)
(1.6) , үйкеліс коэффициенті Стокс заңы бойынша
, үйкеліс коэффициенті Стокс заңы бойынша  . Бұл өрнектерді (1.6) теңдеуге койсақ: ісед.=
. Бұл өрнектерді (1.6) теңдеуге койсақ: ісед.=  (1.7)
(1.7) , мұндағы
, мұндағы 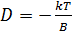
 ; яғни
; яғни  ; ендеше:
; ендеше:  .
.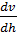 мәндері аз, ал
мәндері аз, ал  және
және  мәндері көп болуы керек. Реалды жағдайларда бұл параметрлерді айтарлықтай өзгерту қиынырақ, ол дисперстік жүйелердегі бөлшектердің радиусы кең аралықта: 10-7-нен 10-2 см-ге дейін өзгереді, сондықтан радиус шешуші роль атқарады. Қарастырылып отырған теңсіздік
мәндері көп болуы керек. Реалды жағдайларда бұл параметрлерді айтарлықтай өзгерту қиынырақ, ол дисперстік жүйелердегі бөлшектердің радиусы кең аралықта: 10-7-нен 10-2 см-ге дейін өзгереді, сондықтан радиус шешуші роль атқарады. Қарастырылып отырған теңсіздік  см болғанда байқалады. Бұл жағдайларда диффузияны елемеуге болады. Ендеше жылдам седиментация жүреді де, жүйе седиментациялық тұрақсыз болады.
см болғанда байқалады. Бұл жағдайларда диффузияны елемеуге болады. Ендеше жылдам седиментация жүреді де, жүйе седиментациялық тұрақсыз болады. ; яғни
; яғни  ; ендеше:
; ендеше:  см болғанда орын алады. Бұл жағдайда седиментацияны елемеуге болады да, ал диффузия бөлшектердің ыдыстың бүкіл көлеміне бірқалыпты таралуын болдырады. Дисперстік жүйе бұл жағдайда седиментациялық тұрақты болады.
см болғанда орын алады. Бұл жағдайда седиментацияны елемеуге болады да, ал диффузия бөлшектердің ыдыстың бүкіл көлеміне бірқалыпты таралуын болдырады. Дисперстік жүйе бұл жағдайда седиментациялық тұрақты болады. , яғни
, яғни  , ендеше
, ендеше