|
|
Роль русских ученых в развитии физической химии.ФИЗИЧЕСКАЯ ХИМИЯ ВВЕДЕНИЕ Физическая химия — наука, объясняющая химические явления на основании физических принципов и законов. В настоящее время она определилась как самостоятельная отрасль науки, обладающая специфическими методами исследования. Физическая химия занимается многосторонним исследованием различных химических реакций и сопутствующих им физических процессов. Как пограничная наука, она изучает объект с нескольких сторон, учитывая диалектический характер взаимосвязи и взаимодействия сложных явлений материального мира. Химические реакции тесно связаны с такими физическими процессами, как электрические явления, теплопередача, поглощение или излучение электромагнитных колебаний. Например, химические реакции, протекающие в гальванических элементах и аккумуляторах, являются причиной возникновения электрического тока. Многие химические реакции сопровождаются выделением или поглощением энергии в виде теплоты, а возникновение других реакций обусловлено действием света. Так, поглощение солнечного света зелеными растениями вызывает сложные реакции фотосинтеза, в результате которых из двуокиси углерода и воды образуются различные органические соединения. Таким образом, физическая химия решает наиболее общие вопросы химии, опираясь на физические законы и методы исследования. Физическая химия включает несколько основных разделов. Строение вещества. Этот раздел физической химии изучает связь между строением веществ и их физическими и химическими свойствами, а также агрегатные состояния веществ. Благодаря достижениям физики и квантовой механики при изучении атомов и молекул в этой области в последние годы наблюдаются значительные успехи. Применение в экспериментальных работах новейших методов молекулярной спектроскопии (включая радиоспектроскопию), а также рентгеноструктурного, электроннографического, электронномикроскопического и других методов исследования дало возможность получить новые данные о строении атомов и молекул, о природе сил, действующих между ними. В учении об агрегатных состояниях рассматриваются вопросы взаимодействия молекул и важнейшие свойства веществ в газообразном, жидком и кристаллическом состояниях. Это учение получило свое развитие на базе кинетической теории материи и статистической физики. Химическая термодинамика. На основе законов термодинамики осуществляются энергетические расчеты химических реакций и химического равновесия, а также определяется возможность и направление самопроизвольного течения того или иного химического процесса. Химическая термодинамика изучает фазовые переходы (растворение, испарение, кристаллизацию и др.), адсорбцию и т. п. Важным разделом химической термодинамики является термохимия, которая изучает тепловые эффекты химических реакций. Этот раздел физической химии имеет большое значение в народном хозяйстве, особенно в области промышленного синтеза. Учение о растворах. В этом разделе изучаются молекулярные структуры растворов, различные их свойства, процессы образования растворов и особенности протекающих в них реакций, а также вопросы растворимости. Электрохимия. Рассматривает важнейшие процессы взаимного превращения электрической и химической форм движения материи, а также свойства и строение растворов электролитов, процессы электролиза, работу гальванических элементов, электрохимическую коррозию металлов, электросинтез веществ и др. В настоящее время электрохимические методы исследования и анализа приобретают все большее значение в практике заводских, агрохимических, почвенных и других лабораторий. Химическая кинетика. Она изучает скорости химических реакций и их зависимости от температуры, давления, концентрации, среды, перемешивания и т. д., а также вопросы катализа гомогенных и гетерогенных химических реакций и способы, позволяющие регулировать и направлять течение различных химических процессов и выход продуктов реакции. В этом разделе физической химии рассматривается также механизм действия биологических катализаторов — ферментов. Фотохимия. Фотохимия изучает процессы воздействия электромагнитных излучений на ход химических превращений. Важными фотохимическими реакциями являются фотосинтез, люминесценция, фотографические и многие другие процессы. Фотохимия тесно связана с учением о строении молекул, а также с химической кинетикой. Таковы основные разделы физической химии. Приведенное деление условно, поскольку каждый физико-химический процесс не только многогранен, но и тесно связан с целым рядом других явлений. Марксистско-ленинский диалектический метод учит, что любое явление материального мира необходимо рассматривать в его тесной и неразрывной связи с окружающими явлениями. Этим объясняется и возникновение физической химии и тесная взаимосвязь различных ее разделов. Необходимо учесть, что всякое реальное движение материи сложно и едино, а разделение его на отдельные формы движения условно и относительно. В силу этого границы между основными разделами физической химии также приблизительны и условны. Перечисленные разделы не охватывают всех областей физической химии. В последние годы в самостоятельные разделы выделены магнетохимия, радиационная химия, физикохимия высокомолекулярных соединений и др. Физическая химия не только всесторонне изучает и обобщает материал по различным разделам химии, она объединяет его, анализирует и выводит общие закономерности развития вечно движущейся материи. В этом заключается общенаучное значение физической химии. Законы, открываемые ею, широко используются общей химией, биологией, геологией, агрохимией, почвоведением и многими прикладными науками. Велико значение физической химии и методов ее исследования в развитии химической технологии. Знание физической химии дает инженеру возможность не только глубоко понять сущность химического процесса, лежащего в основе производства, но и сознательно выбирать и регулировать условия, наиболее благоприятные для проведения нужных процессов. Физическая химия позволяет предвидеть направление химической реакции, а также рассчитать теоретически выход ее продуктов. . Производство новых и высокоэффективных удобрений, разработка и внедрение химических способов борьбы с вредителями и болезнями растений, улучшение водно-физических свойств почвы — эти вопросы могут быть успешно решены лишь на основе знания физической химии. Это убедительно доказали работы советских агрохимиков К. К. Гедройца и Д. Н. Прянишникова. На основании их обширных и разносторонних исследований с применением методов физической химии было создано учение о почвенном поглощающем комплексе, которое получило широкое признание в нашей стране и за рубежом. В настоящее время все большее распространение получают такие физико-химические методы исследования, как термический, рентгенографический, электронномикроскопический, инфракрасно-спектроскопический и многие другие, с помощью которых были получены весьма ценные данные о природе и строении почвенного поглощающего комплекса. Методы электрической проводимости, потенциометрии, криоскопии, фотометрии, эмиссионного анализа и другие также широко применяются в решении основных проблем агрономии. Изучение с помощью физической химии фотохимических реакций позволяет глубже вникать в сущность сложных процессов фотосинтеза. Как известно, из всей солнечной энергии, доходящей до поверхности Земли, энергия, усваиваемая в процессе фотосинтеза всей растительностью земного шара, составляет в среднем только 0,3%. Культурные растения используют солнечную энергию полнее, чем дикие. Используемая ими доля солнечной энергии составляет примерно 0,5—1,5%, а для таких культур, как рис, соевые бобы, сахарная свекла, сахарный тростник, кукуруза и некоторых других, 4— 5% от общего количества солнечной энергии, попадающей на посевы за вегетационный период. Есть основание считать, что полное раскрытие наукой механизма процесса фотосинтеза и овладение управлением им даст возможность повысить коэффициент использования солнечной энергии растениями в два-три раза и более. Такие дисциплины, как агрохимия, почвоведение, физиология растений, микробиология, биохимия, земледелие, защита растений и многие другие, широко используют методы и основные теоретические положения физической химии. Преподавание физической химии в сельскохозяйственных высших учебных заведениях имеет свою специфику. Основной задачей курса является изучение теоретических основ этой науки, знакомство с физико-химическими методами исследования с целью их применения в решении основных вопросов сельского хозяйства.
Роль русских ученых в развитии физической химии. Основателем физической химии является великий русский ученый М. В. Ломоносов (1711 —1765). Ему принадлежит сам термин «физическая химия»; определение задач этой науки было дано им еще в 1752 г., когда он приступил к чтению систематического курса физической химии для студентов Академии наук. Ломоносовым было написано первое учебное пособие «Введение в истинную физическую химию», а также составлена программа экспериментальных работ — «Опыт физической химии» (1754). Задачи, которые должна решать физическая химия, Ломоносов сформулировал следующим образом: «Физическая химия есть наука, объясняющая на основании положений и опытов физики то, что происходит в смешанных телах при химических операциях». Это определение очень близко к современному. Ломоносов выдвинул и обосновал целый ряд положений, которые легли в основу физической химии. Им впервые был открыт закон сохранения материи и движения — один из величайших законов природы. Ломоносов создал стройную кинетическую теорию материи и объяснил теплоту как проявление движения молекул. Он первым указал на невозможность перехода теплоты от холодного тела к горячему и тем самым вплотную подошел к формулировке второго закона термодинамики. Ломоносов впервые ввел в науку представление о молекулах и установил четкое различие между молекулами и атомами. Он объяснил природу газового состояния, высказал мысль о существовании абсолютного нуля температуры, дал правильное толкование процесса растворения как проявления взаимодействия молекул растворенного вещества с. молекулами растворителя, выполнил целый ряд обстоятельных работ по изучению растворов. Русский ученый Г. И. Гесс (1802—1850), профессор Горного института в Петербурге, впервые сформулировал основной закон термохимии «о постоянстве сумм тепла» при химических реакциях. Этот закон, впоследствии названный его именем, следует рассматривать как одно из выражений открытого позднее первого закона термодинамики применительно к химическим реакциям. Большая заслуга в развитии физической химии принадлежит русскому ученому Н. Н. Бекетову (1826—1911), который с 1865 г. возобновил после Ломоносова чтение курса физической химии; он впервые (1865) дал частную формулировку закона действующих масс. Ему принадлежат работы по изучению восстанавливающей способности одних металлов по отношению к другим. Первый в мире учебник по физической химии также был создан в России Н. Н. Любавиным (1845—1918). Ценный вклад в развитие представлений о строении вещества внес основоположник теории химического строения органических соединений А. М. Бутлеров (1828—1886). Для развития химической науки вообще и для физической химии в частности огромное значение имело открытие Д. И. Менделеевым (1834—1907) периодического закона химических элементов (1869), впоследствии названного его именем. Этот закон позволил на основании знания химических свойств одних элементов предвидеть свойства других. Оценивая это открытие Д. И. Менделеева, Ф. Энгельс писал: «Менделеев, применив бессознательно гегелевский закон о переходе количества в качество, совершил научный подвиг, который смело можно поставить рядом с открытием Леверье, вычислившего орбиту еще не известной планеты — Нептуна». Менделеев является также автором гидратной теории растворов, на которой основаны современные исследования в области растворов. Большое значение для развития сельского хозяйства в России имели труды Д. И. Менделеева в области агрохимии. Он впервые поставил задачу широкого использования химии для подъема отечественного сельского хозяйства. Если бы Менделеев не открыл и не разработал периодический закон химических элементов, его имя вошло бы в историю науки и народного хозяйства благодаря фундаментальным трудам в области сельского хозяйства, особенно в области удобрений. Известный русский ученый К. А. Тимирязев проходил сельскохозяйственную практику под руководством Д. И. Менделеева, а Д. Н. Прянишников был учеником и последователем К. А. Тимирязева. Благодаря такой преемственности возникло целое направление в отечественной агрохимии, которое сыграло выдающуюся роль в широком творческом проникновении химии в сельское хозяйство, в его всесторонней химизации (выражение Д. Н. Прянишникова). Большое значение для развития физической химии имели работы И. А. Каблукова (1857—1942), который, исходя из гидратной теории Д. И. Менделеева, установил явление гидратации ионов электролитов в водных растворах и сущность химического взаимодействия в процессах электролитической диссоциации (1891). Им впервые были выполнены работы по исследованию поведения электролитов в неводных растворах. Каблуков организовал первую кафедру физической химии в сельскохозяйственном вузе и начал читать систематический курс физической химии будущим агрономам. Работы Н. С. Курнакова — создателя физико-химического анализа, Н. Д. Зелинского — основателя научной школы органического катализа, Н. А. Шилова, В. А. Кистяковского, Н. А. Изгарышева, а также других ученых заложили прочный фундамент в развитии физической химии. Крупный вклад в развитие физической химии внесли исследования Н. Н. Семенова, разработавшего теорию цепных разветвленных реакций, П. А. Ребиндера, А. Н. Фрумкина, М. М. Дубинина и других ученых, охватывающие область поверхностных и капиллярных явлений. В развитии коллоидной химии большое значение имеют исследования В. А. Каргина, С. М. Липатова, М. М. Дубинина, А. В. Думанского и Н. П. Пескова. Огромное практическое значение для повышения плодородия почв имели исследования К. К. Гедройца — создателя учения о почвенном коллоидно-химическом комплексе, а также Д. Н. Прянишникова, основателя русской школы агрохимиков. Изучение курса физической и коллоидной химии дает теоретическую основу для понимания таких дисциплин, как биохимия, микробиология, агрохимия, почвоведение и др., а знакомство с физико-химическими методами исследования позволяет шире использовать их для решения многих вопросов сельскохозяйственного производства. Настоящее пособие включает в себя описание лабораторных работ по наиболее важным разделам курса физической и коллоидной химии. Кроме того, изучение физической и коллоидной химии дает богатейший материал для формирования научного мировоззрения студентов. Перед выполнением лабораторных работ студенту необходимо изучить основные теоретические положения темы (руководствуясь вопросами самоподготовки), а также ознакомиться с методикой выполнения работы. На занятиях, рассчитанных на 4 часа, осуществляется контроль знаний студентов, после чего дается индивидуальное задание. Составление отчета по выполненной работе делается по следующей форме: 1. Тема, название раздела. 2. Сущность и краткое описание теоретических положений (см. вопросы самоподготовки). 3. Задание. Название лабораторной работы. 4. Цель работы. 5. Методика выполнения работы, зарисовка схем установки и приборов. 6. Результаты экспериментальных измерений в таблицах. 7. Расчеты и, если требуется, графические построения. 8. Анализ результатов наблюдений. 9. Выводы согласно цели задания. При работе в лабораториях физической и коллоидной химии необходимо соблюдать правила.
ПРАВИЛА РАБОТЫ В ЛАБОРАТОРИЯХ ФИЗИЧЕСКОЙ И КОЛЛОИДНОЙ ХИМИИ
В лаборатории необходимо находиться в халате, во время работы соблюдать чистоту и правила техники безопасности (см. плакаты и инструкции по технике безопасности). Концентрированные кислоты и щелочи содержатся в склянках, снабженных капельницами. Растворы разбавленных кислот и щелочей, аммиака и других вредных веществ следует отбирать цилиндрами или пипетками, непременно снабженными грушами. Перед включением устройств и приборов необходимо проверить правильность составления схемы, исправность приборов, розеток и выключателей. Строго выполнять указания преподавателя. Оборудование, детали к приборам и методические указания для выполнения работ получает дежурный группы у лаборанта или сам студент под студенческий билет или зачетную книжку. По всем вопросам отсутствия на рабочих местах реактивов, посуды, а также неисправности приборов обращаться к дежурному лаборанту. Бережно относиться к лабораторному оборудованию, приборам и посуде. Экономно расходовать реактивы, дистиллированную воду, фильтровальную бумагу и т.п. Экономить электроэнергию, холодную и горячую воду. По окончании работ не забывать выключать приборы, вымыть посуду, убрать рабочее место и сдать его лаборанту.
Математические понятия. Цель этого приложения — дать общее представление о математических понятиях, используемых при изучении курса, а также для расчетов при выполнении лабораторных работ. Логарифмы Определение 1. Пусть а и b — положительные действительные числа (b ≠ 1). Показатель степени р, в которую нужно возвести b, чтобы получить а, называется логарифмом числа а по основанию b. Символ logba = p означает, что bр = а. Пример А. 1. Поскольку 23 = 8, 1оg2 8 = 3. Пример А.2. Поскольку 8⅔ = 4, 1оg8 4 =⅔. Пример А.З. Поскольку 10 – 2 =0,01, lоg10 0,01 =-2. Пример А.4. Найдем b, если 1оgb 9 = 2. Решение: Из определения 1 следует, что b2 = 9, поэтому b = 3. (Замечание: b = – 3 тоже является решением уравнения b2 = 9, но по определению основание должно быть положительным.) Пример А.5. Найдем х, если 1оg10 x = – 1/2. Решение: x = 10 –1/2 = 1/ √10 Требование отличия основания логарифма от 1 необходимо в определении, потому что 1 в любой степени есть 1. Кроме того, поскольку любая степень положительного числа есть положительное число, логарифм отрицательных чисел не определен. Логарифм нуля также не определен. На практике обычно используются две системы логарифмов — натуральные логарифмы и десятичные логарифмы. Десятичные логарифмы имеют основание 10, а натуральные — число е. (Число е — это иррациональное число, приблизительно равное 2,718). Для того чтобы каждый раз не указывать величину основания логарифмов, мы не будем пользоваться индексами и будем обозначать, как принято, loge х и 1оg10x соответственно 1n х и lg х. Свойства логарифмов 1. logb x + logby = logb(xy). 2. logb x – logby = logb(x/y). 3. k logb x = logb(xk). 4. blogbx = x. 5. logax = (logab) ∙ logbx. Поскольку 1n10 ≈2,3026 (т.е. натуральный логарифм 10 приблизительно равен 2,3026), по свойству 5 имеем:
ln x ≈ 2,3026 1g х.
Любое число, выраженное в виде десятичной дроби, может быть записано в «стандартной» форме как произведение целой степени 10 и числа между 1 и 10. Так, например, 0,002 = 2 ∙ 10 – 3; 352 = 3,52 ∙ 102; 4,32 = 4,32 ∙ 100. Благодаря свойству логарифмов 1 : 1g 0,002 = 1g 2 + 1g 10 – 3 = 1g 2 – 3; lg 352 = lg 3,52 + lg 102 = lg 3,52 + 2; lg 4,32 = lg 4,32 + lg 100 = lg 4,32 + 0. Эти замечания иллюстрируют общее положение, согласно которому всякий десятичный логарифм можно выразить в виде суммы целого числа и логарифма числа, заключенного между 1 и 10. Последний логарифм сам является числом, заключенным между 0 и 1, и поэтому приближенно может быть выражен положительной десятичной дробью. Эта десятичная дробь называется мантиссой, причем таблицы десятичных логарифмов и представляют собой таблицы мантисс. Показатель степени 10, который входит в стандартную форму числа, называется характеристикой. Таким образом, характеристика числа 0,002 есть – 3, характеристика 352 есть 2, а характеристика 4,32 есть 0. В вычислениях с логарифмами принято писать отрицательные характеристики в так называемой форме 9 – 10. В этой форме 1g 0,002 = 7,3010 – 10. Данное выражение можно записать также в виде 1g 0,002 = Пример А.6. Найдем 1g 352. Решение: 352 = 3,52 ∙ 102; 1g 352 = 1g 3,52 + 1g 102.
Из таблиц 1g 3,52 = 0,5464, а по определению 1g 102 = 2. Таким образом,
1g 352 = 2 + 0,5464 = 2,5464.
Пример А.7. Найдем 1g 0,002. Решение:
1g 0,002 = 1g (2 ∙ 10 – 3) = 1g 2 + lg 10 – 3 = 0,3010 + (–3) = – 2,6990.
Пример А. 8. рН раствора представляет собой отрицательный десятичный логарифм [Н+], где [Н+] — активность ионов водорода (приблизительно равная концентрации ионов водорода, выраженной в г–ион/л), т.е. рН = – 1g[Н+]. Найдем, чему равен рН раствора, если [Н+] = 0,000243. Решение: рН = – 1g (0,000243) = – 1g (2,43 ∙ 10 – 4) = – (0,386 – 4) = 3,614.
Для того чтобы найти число по известному логарифму, можно использовать аналогичный подход. Пример А. 9. Найдем [Н+], если рН = 2,602. Решение:
– lg [Н+] = 2,602 1g [Н+] = – 2,602 = 0,398 – 3.
Из таблиц находим, что 0,398 = 1g 2,5, поэтому
[Н+]=2,5 ∙ 10 – 3 = 0,0025.
Перед тем как обратиться к таблицам, мы выразили – 2,602 в виде суммы положительной десятичной дроби и целого числа – 3, поскольку таблицы содержат только положительные десятичные дроби. Пример А. 10. Для того чтобы найти рН, с помощью рН – метра измеряют электрическое напряжение ξ и по формуле рН = ξ – 0,336/ 0,059 получают величину рН. Найдем [Н+], если ξ = 0,525. Решение: ξ = 0,525 – 0,336/0,059 = 3,20.
–lg[Н+] = 3,20, lg[Н+] = – 3,20 = 0,80 – 4, [Н+] = 6,3 ∙ 10-4.
Пример А. 11. Для того же рН – метра, что и в предыдущем примере, определим, какое значение ξ соответствовало бы концентрации ионов водорода 2,3 ∙ 10 – 7. Решение: рН = – 1g [Н+] = – 1g (2,3 ∙ 10 – 7) = – (0,3617 – 7) = –(– 6,6383) = 6,6383. Подставляя полученное значение рН в формулу, приведенную в примере А. 10, находим ξ : ξ – 0,336/0,059 = 6,638; ξ = 0,059 ∙ 6,638 + 0,336 = 0,728. Логарифмические графики Выражение концентрации водородных ионов в логарифмической форме (рН) может служить примером того, как логарифмы могут упростить проблему графического представления соотношений между физическими величинами. Если вдоль одной из осей откладывать [Н+], то построить график для области значений [Н+] в пределах от 10 – 4 до 104 практически невозможно. Если же откладывать величину –1g[Н+], то этот же интервал концентраций ионов водорода займет всего лишь область от –4 до +4. При графическом представлении физических величин часто желательно получать графики в виде прямых линий. Иногда это достигается откладыванием логарифма одной или обеих переменных.
Рис. А.2.
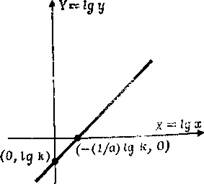
Рис. А.4.
Пример А. 12. На рис. А. 1 представлен график соответствующий уравнению у = а∙bx, где а и b — положительные константы. На рис. А.2 приведен график, который получается, если по одной оси отложить Y, а по другой х, где Y=lg y. Поскольку зависимость lg y = lg а + x lg b линейна для х, уравнение Y =lg а + х lg b дает на графике прямую линию. (Этот способ называют изображением зависимости y от x в полулогарифмическом масштабе.). Пример А. 13. График, соответствующий уравнению у = k∙xa, где а и k – константы, показан на рис. А. 3. Логарифмируя обе части уравнения, получаем lg y = lg k + a lg x. Если обозначить Y = lg у и Х = lg x, то уравнение окажется линейным по X и Y. График, выражающий зависимость Y от X, имеющий вид прямой линии, представлен на рис. А. 4. (Этот способ называют изображением зависимости у от х в логарифмическом масштабе.)
Формулы для интегрирования 1.∫ c du = c ∫ du, (с — постоянная).
2.∫ (u + υ) dх =∫u dх + ∫ υ dх. Пример: ∫ (x2 + 4) dх =∫ х2 dх + ∫ 4 dx = x3/3 + 4x + c.
3. Если n ≠ – 1, то ∫ un du = un + 1/n + 1 + c.
Пример: ∫ dx/x3 = ∫ x –3 dx = x –2/–2 + c = –1/(2x2 + c).
4. ∫ u – 1 du = ∫ du/u = ln |u| + c, u ≠ 0.
Пример: ∫ dp/(p – 4) = ln | p – 4 | + c.
Замечание. Символ |u| читается: «абсолютное значение u». Вертикальные черточки означают, что мы должны использовать u, если u ≥ 0, и – u, если u < 0. Если мы встречаемся с множеством значений р > 4, то ln | р – 4 | = ln (р – 4) . Но если значения р < 4, то ln | р – 4 | = ln (4 – р) .
5. ∫ eu du = eu + c. Пример: ∫ e3x dx = 1/3 ∫ e3x d(3x) = 1/3e3x + c.
Определенный интеграл b Числа а и b в символе ∫а называются соответственно нижним и верхним пределами интегрирования.
b Пример. Вычислим ∫ х dх. a Решение. Поскольку ∫ x dх = х2/2 + С, исходя из теоремы, имеем b ∫ x dx = (b2/2 + C) – (a2/2 + C) = (b2 – a2)/2. a 1 Пример .Вычислим ∫ (1/ x + 1) dx Решение. 1 Поскольку ∫ (1/ x + 1) dx = ln (x + 1) + C, получаем ∫ (1/ x + 1) dx = [ln (x + 1)] = ln 2 – ln 1 = ln 2. 0
ТЕМА I |
|
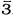 ,3010, где черта над 3 означает, что характеристика равна – 3, а десятичная часть + 0,3010. Оба равенства означают, что 1g 0,002 = 0,3010 – 3 = – 2,6990.
,3010, где черта над 3 означает, что характеристика равна – 3, а десятичная часть + 0,3010. Оба равенства означают, что 1g 0,002 = 0,3010 – 3 = – 2,6990. Рис.А.1.
Рис.А.1. 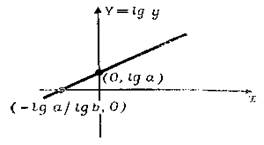
 Рис.А3
Рис.А3