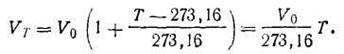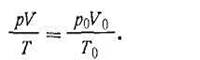|
|
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ТРЕХ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВАОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ И ТЕРМОХИМИИ Агрегатное состояние вещества. Понятие о плазме. В зависимости от внешних условий (температуры и давления) почти каждое вещество может находиться в газообразном, жидком или твердом состоянии. Это — агрегатные состояния вещества. Агрегатное состояние обусловлено различиями в характере теплового движения молекул (атомов) вещества и в их взаимодействии. Переходы между агрегатными состояниями вещества сопровождаются скачкообразными изменениями свободной энергии, энтропии, плотности и других основных физических свойств. В газообразном состоянии вещество обладает способностью расширяться и стремится занять весь предоставленный ему объем. Его молекулы почти не взаимодействуют, так как находятся на сравнительно больших расстояниях друг от друга. При повышении давления газы легко изменяют свой объем. Жидкость принимает форму заключающего ее сосуда, но сохраняет постоянным свой объем. В жидкостях молекулы находятся значительно ближе друг к другу, а силы межмолекулярных взаимодействий больше, чем в газах. Однако молекулы жидкостей, как и газов, не закреплены в определенных точках пространства и находятся в хаотическом поступательном движении. Их тепловое движение представляет собой сочетание малых колебаний около положений равновесия и частых перескоков из одного положения равновесия в другое. Этим и объясняются свойственные жидкому состоянию подвижность и текучесть. При повышении давления жидкости лишь незначительно изменяют свой объем, поскольку этому препятствуют силы электростатического отталкивания молекул, увеличивающиеся при их сближении. Поэтому жидкости практически несжимаемы. Твердое вещество имеет собственную форму и объем. Силы притяжения между молекулами в твердых телах уравновешиваются силами отталкивания. Этим, например, объясняется геометрически правильное расположение частиц кристалла в определенных точках пространства, образующих пространственную кристаллическую решетку. Частицы твердого тела в кристаллическом состоянии утрачивают свободу поступательного движения и испытывают только колебательные движения в узлах кристаллической решетки. Твердое вещество может находиться в кристаллическом и аморфном состоянии. Для того чтобы нагляднее представить себе различия между кристаллическими и аморфными веществами, а также между твердыми телами и жидкостями, рассмотрим более подробно вопрос об упорядоченности во взаимном расположении атомов или молекул в них. Упорядоченность, которая проявляется на расстояниях, сравнимых с межатомными, является упорядоченностью ближнего порядка, а упорядоченность, повторяющаяся на неограниченно больших расстояниях,— дальнего порядка. Как известно, в газах (точнее, в идеальных газах) расположение молекулы в какой-либо точке пространства не зависит от расположения других молекул, т. е. в них отсутствует дальний и ближний порядок. Что же касается жидкостей и аморфных тел, то в них уже существует ближний порядок, характеризующийся некоторой закономерностью в расположении соседних атомов. Дальний порядок в жидкостях и аморфных телах отсутствует, так как на больших расстояниях этот порядок «размывается» и постепенно переходит в «беспорядок». В твердых кристаллических телах атомы (или молекулы) расположены правильными рядами, сетками (пространственными решетками) и для сколь угодно отдаленных атомов повторяется правильное чередование их на одних и тех же расстояниях друг относительно друга. Другими словами, в твердых кристаллических телах существует не только ближний, но и дальний порядок во взаимном расположении атомов или молекул. Характерными признаками дальнего порядка являются: симметрия и закономерность в расположении частиц, Не все вещества могут находиться во всех трех агрегатных состояниях. Для некоторых веществ возможны только одно или два агрегатных состояния. Так, карбонат кальция СаСО3 практически невозможно получить ни в жидком, ни в газообразном состояниях, поскольку при нагревании он разлагается на нелетучую окись кальция и газообразную двуокись углерода. Другие вещества при определенных условиях могут находиться одновременно в двух или даже трех агрегатных состояниях. Так, вода при давлении 6,14·102 Па и температуре 273,1675 К находится в устойчивом равновесии в трех состояниях: твердом (лед), жидком (жидкая вода) и газообразном (водяной пар). Переход вещества из жидкого состояния в газообразное называется парообразованием, из твердого в газообразное — сублимацией и из твердого в жидкое — плавлением. Обратные процессы перехода соответственно носят название сжижения, десублимации и отвердевания. Все эти процессы, как правило, сопровождаются выделением теплоты (теплоты парообразования, сублимации, плавления и т. д.). Постепенно изменяя внешние условия (температуру и давление), можно осуществлять переход из одного агрегатного состояния в другое. С изменением температуры и давления постепенно изменяются расстояния между частицами в веществе, таким образом изменяется количественная сторона, а на определенном этапе в результате скачка вещество приобретает новое качество, т. е. переходит в новое агрегатное состояние. Агрегатные состояния, по выражению Энгельса, — узловые точки, где количественное изменение переходит в качественное.
Основные газовые законы. Сила взаимодействия между молекулами, как известно, зависит от расстояния между ними. Силы межмолекулярного взаимодействия (так называемые силы когезии) за пределами расстояния, большего 10-7 см от центра молекулы, настолько ослабевают, что ими можно пренебречь. Средней кинетической энергии теплового движения молекул газа вполне достаточно, чтобы преодолеть силы когезии (силы межмолекулярного взаимодействия). При столкновении молекул друг с другом, когда одна молекула попадает в силовое поле притяжения другой молекулы, между ними возникает мгновенное когезионное взаимодействие. Чем больше давление, тем больше число столкновений молекул газа в 1 с, а следовательно, и суммарные мгновенные когезионные взаимодействия между ними оказывают большее влияние на свойства данного газа. И наоборот, в состоянии сильного разрежения размеры молекул по сравнению с межмолекулярными расстояниями и силы взаимодействия между молекулами ничтожны. В силу хаотического движения молекул газа концентрация их в любой части занимаемого газом пространства одинакова, как и плотность его во всей массе. Однако это справедливо лишь в том случае, если речь идет о средней плотности газа в макрообъеме. В микрообъеме же вследствие хаотичности молекулярного движения могут происходить значительные отклонения от средней плотности. Это явление называется флуктуацией (лат. fluctuatio — колебание). Флуктуационные отклонения плотности тем больше, чем меньше микрообъем. В отдельных случаях они могут достигать 20% и более по сравнению со средней плотностью газа во всей его массе. Газы широко распространены в природе и используются в различных отраслях народного хозяйства в качестве топлива, теплоносителей, сырья для химической промышленности, рабочего тела для выполнения механической работы (газовые турбины) и во многих других случаях. Отсюда вытекает необходимость знания законов, которым подчиняются газы. Основные газовые законы выведены для идеального газа. Идеальным называется газ, находящийся в таком состоянии, при котором можно пренебречь силами межмолекулярного взаимодействия и собственным объемом его молекул. Свойства идеального газа, таким образом, определяются температурой и давлением, при которых газ находится в данный момент. Газы, реально существующие в природе (реальные газы), в большей или меньшей степени отступают от газовых законов. Закон Бойля-Мариотта. Объем данной массы газа (V) при постоянной температуре изменяется обратно пропорционально давлению (р), под которым газ находится:
или p1V1 = p2V2. Аналогичное равенство можно написать и для других значений р и V:
Отбросив индексы, получим:
при условии, что t = const. Таким образом, произведение объема газа на его давление при постоянной температуре есть величина постоянная. Величина константы в уравнении (1.2) зависит от природы газа, его количества и температуры, но не зависит от изменения объема или изменения давления. Из закона Бойля-Мариотта вытекает следующее: концентрация и плотность данной массы газа изменяются при постоянной температуре прямо пропорционально изменению давления и обратно пропорционально изменению объема. Таким образом, исходя из уравнения (1.1) можно записать:
Закон Гей-Люссака. При нагревании данной массы газа на 1 К при постоянном давлении объем его увеличивается на 1/273,16 часть того объема, каким обладал бы газ при 273,16 К и при том же давлении. Так, если объем газа при 273,16 К был V0, при нагревании газа на ∆T градусов стал Vт, а прирост объема ∆V, то
Или
В уравнении (1.6) величина 1/273,16 =a, носит название коэффициента термического расширения. Этот коэффициент не зависит от природы идеального газа, его давления, объема и температуры. Таким образом,
Если объем газа остается постоянным, то по такому же закону растет и давление:
В этом случае величина a, равная 1/273,16, называется термическим коэффициентом упругости газа. Математическую зависимость, выражающую закон Гей-Люссака, можно значительно упростить, если в уравнение (1.5) вместо ∆Т ввести Т. Учитывая, что
преобразуем уравнение (1.5) следующим образом:
Отбросив индексы и объединив постоянные величины в одну константу, получим V = const T при р = const. Аналогично можно преобразовать и уравнение (1.8), получив р = const Т при V = const. На основании приведенных уравнений можно сделать вывод: объем и давление изменяются прямо пропорционально изменению термодинамической температуры газа:
Графически закон Гей-Люссака выражается пучком прямых линий, выходящих из начала координат. Из закона Гей-Люссака вытекает: плотность и концентрация газа, находящегося под постоянным давлением, обратно пропорциональны термодинамическим температурам
Закон Авогадро. В равных объемах различных газов при одинаковой температуре и давлении содержится одинаковое число частиц (молекул или атомов). Из закона Авогадро вытекает важное следствие. Число молекул, которое содержится в одном киломоле любого газа, есть величина постоянная: N0= 6,02·1026 (постоянная Авогадро). Полезно отметить, что термин кмоль определяется как 6,02·1026 «формульных единиц» (не обязательно молекул!). Следовательно, при одинаковых условиях 1 кмоль любого газообразного вещества должен занимать постоянный объем. Так, при нормальных условиях (T = 273,16 К; р= 101 325 Па) 1 кмоль любого газа занимает объем 22,4 м3. Этой величиной часто пользуются в расчетах. Состояние газа характеризуется тремя величинами: давлением р, объемом V и температурой Т. Эти три величины связаны уравнением, которое получило название уравнения состояния идеального газа. Оно выводится путем объединения законов Бойля-Мариотта, Гей-Люссака и Авогадро. Если 1 кмоль газа при нормальных условиях (р0, Т0 и V0) нагреть до определенной температуры Т при том же давлении, то согласно закону Гей-Люссака объем газа при этой температуре VT будет равен:
Если при постоянной температуре Т изменить давление газа от р0 до любого значения р, то объем газа также изменится и станет равным V. На основании закона Бойля-Мариотта pV = p0VТ. Подставив в это уравнение значение VТ (I.11), получим pV = Tp0V0 /T0, откуда
Поскольку p0, V0 и Т0 — величины постоянные, отношение PoVo/To есть также величина постоянная для всех газов независимо от их химической природы. Эту постоянную величину обозначают буквой R и называют универсальной газовой постоянной. С учетом этого уравнение (I.15) преобразится:
Уравнение (I.16) справедливо для 1 кмоль газа. Если в объеме газа будет содержаться n кмоль, то это уравнение будет иметь более общий вид:
Уравнение (I.17) является основным уравнением газового состояния и называется уравнением Клапейрона - Менделеева. Впервые это уравнение было выведено Клапейроном в 1834 г. Д. И. Менделеев в своих работах в 1874 г. указал, что благодаря закону Авогадро уравнение Клапейрона приобретает наибольшую общность, когда оно относится не к обычной единице массы (грамму или килограмму), а к 1 кмоль газа. Число киломолей газа n можно рассчитать по формуле
где m — масса газа, содержащегося в объеме V при давлении р и температуре Т ; М — масса киломоля газа. Подставив значение n в уравнение (I.17), получим
Откуда
Отношение m/V есть не что иное, как плотность газа d, откуда d = Mp/RT. Если обе части уравнения (I.20) разделить на объем V, получим
Поскольку отношение n/V есть концентрация газа С, то уравнение Клапейрона - Менделеева будет иметь вид:
Численное значение универсальной газовой постоянной зависит от того, в каких единицах измерены нормальное давление р0 и объем V0 одного моля таза.
|
|

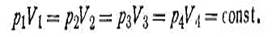



 где С1, С2 и d1,d2 - соответственно концентрации и плотности данной массы газа.
где С1, С2 и d1,d2 - соответственно концентрации и плотности данной массы газа.