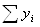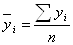|
|
Изучение сезонных колебаний в деятельности торгового предприятияПрименение формул для изучения сезонных колебаний проиллюстрируем на примере одного из торговых предприятий. Имеются данные о продаже молочных продуктов в одном из магазинов по кварталам 2000 – 2003 гг. Таблица 2– Среднедневная реализация, молочных продуктов, т
Необходимо вычислить индексы сезонных колебаний реализации данных продуктов. Из таблицы 2 видно, что в 2003 г. рост продажи молочных продуктов по сравнению с 2000 г. достиг 152,6%, или в среднем за год интенсивность роста составила 115,1%
Выводы о значительном росте реализации данной продукции в 2000 – 2003гг. предопределяет выбор формулы для расчета индексов сезонности способом переменной средней.По содержащимся в таблице 2 показателям анализируемого ряда динамики можно выдвинуть рабочую гипотезу о возможных типах математических функций для получения теоретических уровней тренда. С известной степенью приближения это может быть прямолинейная функция: Yt = a0+a1t (5) В основе такого предположения лежит характер изменения абсолютных приростов. При общем среднем абсолютном приросте 10,9m((94.6 – 62.0) / 3) отклонения по отдельным годам не столь значительны: -0,7m в 2001 г. и +0,7m в 2002 г. Но при наибольшем абсолютном приросте в 2002 г. (+11,6m) в 2003 г. было снижение этого показателя до 10,8m. Эта максимальная интенсивность роста продажи данного продукта в 2002 г. и последующее снижение в 2003 г. отображает показатель темпа наращивания, %: 16,5 < 18,7 > 17,4. Цепные темпы роста показывают затухание интенсивности реализации данной продукции из года в год: 116,5 > 116,1 > 112,9. Все эти показания анализируемого ряда динамики позволяют сделать предположения о возможном применении в аналитическом выравнивании параболы второго порядка: Yt = a0+a1t + a2t2 (6) Таким образом, на основе статистических показателей изменений уровней анализируемого ряда динамики сделано предположение о возможном применении в аналитическом выравнивании исходных данных двух математических функций Для решения вопроса о том, какая их них является адекватной, может применяться критерий минимальности стандартной ошибки аппроксимации: σy= (√∑(yt-yi)2) / n (6) Для этого, прежде всего, должны быть решены выбранные математические функции. Для определения параметров уравнений составляется матрица расчетных показателей (таблица 3). Таблица 3 – при St=0
Рассчитаем параметры линейной функции: ɑo = ∑y / n = 1250, 5 / 16 = 78, 16
ɑ1 = (∑txy) / (∑t2) = 1856,7 / 1360 = 1,365
Уравнение линейной функции примет вид:
Yt= 78,16 + 1,365t (7) Производится расчет теоретических уровней тренда для каждого периода анализируемого ряда динамики 2000 г. YI = 78,16 + 1,365 x (-15) = 57,68
YII = 78,16 + 1,365 x (-13) = 60,41
2003 г. YIV = 78,16 + 1,365 x 15 = 98,63 Полученные теоретические значения уровней тренда Рассчитаем параметры для функции параболы второго порядка: ɑ0 = (∑t4∑y - ∑t2∑t2y) / (n∑t4 - ∑t2∑t2) = (206992 x 1250,5 – 1360 x 106352,9) / (16 x 206992 – 1360 x 1360) = 78,1
ɑ1 = (∑txy) / ∑t2 = 1856,7 / 1360 = 1,365
ɑ2 = (n∑t2y - ∑ t2∑y) / (n∑t4 - ∑t2 ∑t2) = (16 x 106352,9 – 1360 x 1250,5) / (16 x 206992 – 1360 x 1360)
Уравнение параболы второго порядка примет вид: Yt = 78,1 + 1,365t + 0,0007t2 (3.5) По модели (3.5) рассчитываются теоретические уровни для каждого периода анализируемого ряда динамики 2000 г. YI = 78,16 + 1,365 + 0,0007 = 57,78 YII = 78,16 + 1,365 + 0,0007 = 60,47 2003 г. YIV = 78,16 + 1,365 =0,0007 = 98,73 Полученные теоретические уровни тренда записаны в гр. 5 табл. 3.3. Для определения показаний стандартной ошибки аппроксимации составляется матрица расчетных показателей (табл. 4). Таблица 4 – Матрица расчетных показателей для определения стандартной ошибки аппроксимации
По итоговым данным гр. 7 и 9 табл. 4 определяется по формуле ошибка аппроксимации 1) для модели Yt = 78,16 + 1,365t σy=√8109,7/16 = ± 22,51: 2) для модели Yt = 78,1 + 1,365t + 0,0007t2 σy=√8129,7/16 = ± 22,54 Из сравнения вычисленных значений стандартной ошибки аппроксимации следует, что по критерию минимальности предпочтительнее будет трендовая модель , синтезированная на основе прямолинейной функции. Поэтому определение индексов сезонности реализации данной продукции следует осуществлять на базе теоретических уровней тренда, вычисленных по модели:Yt = 78,16 + 1,365t. Теоретические уровни тренда анализируемого ряда динамики изображены на графике (см. рис. 3.1) в виде пунктирной прямой линии. Для определения индексов сезонности Таблица 5
В гр. 4 таблицы 5 определены индивидуальные индексы сезонности Для элиминирования действия факторов случайного порядка производится усреднение индивидуальных индексов сезонности. Для этого по формуле I кв.: (86,5 + 70,1 + 64,0 + 67,1) / 4 = 71,9% II кв.: (125,4 + 129,4 + 129,5 + 129,4) / 4 = 128,4% III кв.: (117,0 + 126,1 + 128,0 + 132,1) / 4 = 125,8% IV кв.: (73,6 + 71,8 + 78,4 + 71,5) / 4 = 73,8% Вычисленные средние индексы сезонности составляют модель сезонной волны реализации молочной продукции во внутригодовом цикле. Наибольший объем продаж приходится на II и III кварталы с превышением среднегодового уровня соответственно на 28,4 и 25,8%. В I и IV кварталах происходит снижение среднегодового уровня соответственно на 28,1 и 26,2%. Более наглядно полученная модель сезонной волны может быть представлена графически (рис. 3.2).
Покажем расчет индексов сезонности способом постоянной средней на примере данных о товарообороте торгового предприятия (табл. 3.5). Таблица 6– Среднедневной товарооборот, тыс. руб.
Необходимо определить индексы сезонности товарооборота. Так как среднегодовой темп роста составил Тр = √74,4 / 73,4 = 1,007 или 100,7%, то в данном случае нет значительной тенденции роста. Следовательно, используем способ постоянной средней. Исчислим средние уровни одноименных внутригодовых периодов для января ух= (68,4 + 72,8 + 65,1) / 3 = 68,8 тыс. руб.; для февраляyф= (69,3 + 73,4 + 66,5) / 3 = 69,7 тыс. руб. и т. д. Для каждого месяца эти значения определены в гр. 6 табл. 3.6. Таблица 7
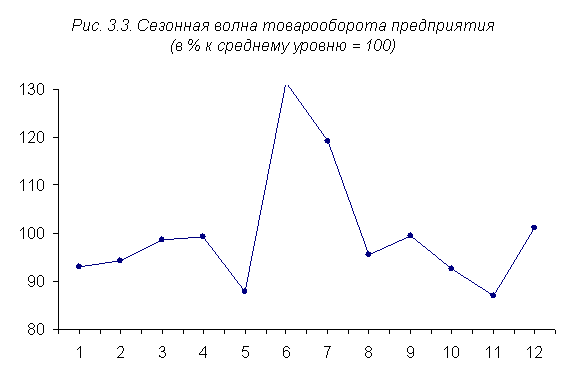
В итоговой строке гр. 6 определен знаменатель формулы в виде общего для всего ряда динамики среднего уровня: y = (68,8 + 69,7+ 72,9 + 73,4 + 64,9 + 97,4 + 88,1 + 80,6 + 73,5 + 68,4 + 64,4 + 74,8) /12 = 73,9 тыс. руб. Этот общий средний уровень и используется в качестве постоянной базы сравнения при определении средних индексов сезонности, которые помещены в гр. 7 табл. 3.6: Is = 68,8 / 73,9 x 100 = 93,1%; Is = 69,7 / 73,9 x 100 = 94,3% и т. д. Из гр. 7 видно, что сезонные колебания товарооборота предприятия характеризуются повышением в июне (+31,4%), июле (+19,2%) и декабре (+1,2%) и снижением в других месяцах. Для большей наглядности сезонных колебаний средние индексы изобразим графически (рис. 3.3).
Вывод: Сезонность и сезонные колебания вызываются различными причинами. Но как в производстве, так и в обращении сезонные колебания отрицательно сказываются на развитии экономики страны, обуславливают неравномерность использования трудовых ресурсов и оборудования в течение года, а это в свою очередь приводит к понижению производительности труда и повышению себестоимости изготовляемой продукции. Сезонные колебания в одних отраслях экономики вызывают соответствующие колебания в других, иначе говоря, проблема сезонности является общей проблемой экономики Российской Федерации. Неравномерность производства того или иного продукта обуславливает соответствующую неравномерность его потребления, потребление в свою очередь оказывает воздействие на производство. Но не всякая сезонность преодолима и не всякая сезонность требует преодоления. С увеличением и расширением производства товаров, с ростом благосостояния населения сезонность продажи непродовольственных товаров увеличивается, а сезонность продажи и потребления продовольственных товаров снижается. Сезонные колебания, отраженные в рядах динамики, необходимо изучать и измерять для учета определения мероприятий, необходимых для уменьшения (или увеличения) сезонных колебаний. Задача 1.Осуществите анализ сезонных колебаний товарооборота по данным таблицы Таблица 1– Анализ сезонных колебаний товарооборота
Контрольные вопросы: 1. Понятие о внутригодовой динамике социально-экономических явлений в деятельности предприятия торговли. 2. Статистические методы выявления сезонных колебаний. 3. Изучение сезонных колебаний в деятельности торгового предприятия.
Практическое занятие 11 Тема:Анализ поступления товаров Цель занятия:проанализировать поступление товаров на предприятие |
|
 . Это позволяет считать, что в анализируемом году динамики имеется значительная тенденция роста. Графическое изображение исходной информации подтверждает эти выводы (рис. 3.1).
. Это позволяет считать, что в анализируемом году динамики имеется значительная тенденция роста. Графическое изображение исходной информации подтверждает эти выводы (рис. 3.1).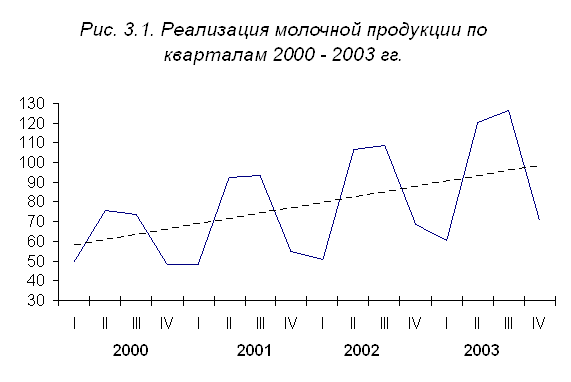






 :
:


 :
: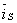 используется следующая матрица расчетных показателей (таблица 5).
используется следующая матрица расчетных показателей (таблица 5).
 , характеризующие отношение эмпирических уровней
, характеризующие отношение эмпирических уровней  производится расчет средних индексов сезонности по одноименным кварталам
производится расчет средних индексов сезонности по одноименным кварталам  анализируемого ряда внутригодовой динамики:
анализируемого ряда внутригодовой динамики: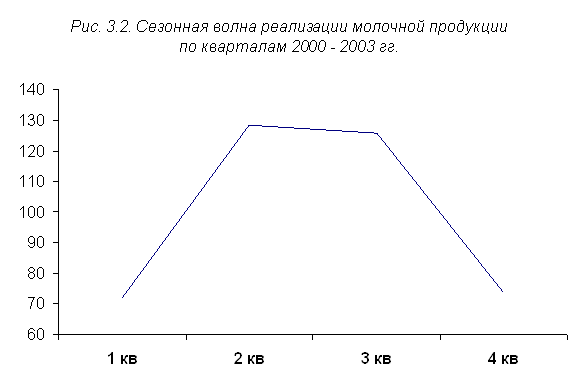
 :
: