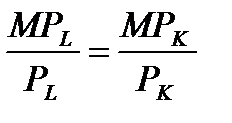Производство в долгосрочном периоде

В долгосрочном периоде все ресурсы являются переменными, так как у предпринимателя достаточно времени для того, чтобы изменить их объем. Факторы производства в определенной степени могут заменять друг друга, поэтому предпринимателю нужно выбрать такую технологию, которая позволит минимизировать издержки производства. Предположим, что фирма использует 2 переменных ресурса: труд (L) и капитал (K). В такой модели рациональный предприниматель будет вести себя аналогично рациональному потребителю и сопоставит предельную отдачу ресурсов (выигрыш) с затратами на их приобретение. Формула минимизации издержек будет выглядеть следующим образом:

MP_L / P_L = MP_K / P_K,

где MP_L и MP_K – предельный продукт труда и капитала, а P_L , P_K - их цены.

Данная формула означает, что отдача на последний рубль (доллар, евро) издержек должна быть одинаковой для каждого ресурса. Если на вложенный рубль предельный продукт труда будет больше, чем предельный продукт капитала, предприниматель будет нанимать больше работников и сократит количество используемого капитала. И наоборот.

Подобный вывод может быть получен не только на основе принципов маржинализма, но и путем анализа изоквант и изокост.

Изокванта –кривая, состоящая из различных комбинаций труда и капитала, использование которых обеспечивает одинаковый объем выпуска продукции.

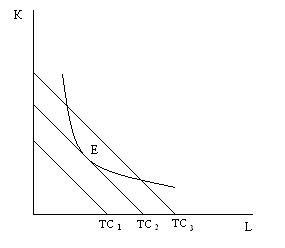
Рис.16. Изокванты.

По существу и графически изокванта напоминает кривую безразличия. Действительно, предпринимателю безразлично, какую комбинацию ресурсов применить – А, В, С, так как в любом случае будет произведен одинаковый объем. Совокупность изоквант называется картой изоквант. Изокванты обладают теми же свойствами что и кривые безразличия. Они никогда не пересекаются. Чем выше расположена изокванта, тем большему объему выпуска она соответствует. Изокванты выгнуты к началу координат и становятся более пологими по мере продвижения вправо вследствие эффекта убывания предельного продукта. Наклон изокванты характеризует предельную норму технологического замещения MRTS.MRTS–количество единиц одного ресурса, которым можно заменить единицу другого ресурса, не меняя объема производства. Наклон изокванты в разных точках не одинаков и равен отношению предельных продуктов двух факторов.

По мере движения по изокванте вправо MRTS сокращается.

Издержки производства могу быть представлены в виде изокосты – линии, объединяющей различные комбинации труда и капитала, которые можно приобрести при фиксированном уровне расходов. Эти расходы составляют общие издержки ТС. Поэтому изокосту можно назвать прямой равных издержек. Она аналогична бюджетной линии потребителя. Ее уравнение можно представить как

TC = P_L·L +P_K·K

Для каждого значения ТС уравнение графически выражается удельной изокостой. Их совокупность образует карту изокост. Наклон изокосты постоянен вдоль всей прямой и равен ценовому отношению обоих факторов: P_L / P_K.

Изменения относительных цен капитала и труда изменяют и угол наклона изокосты. Предположим, что цена капитала увеличится, тогда угол наклона изокосты уменьшится, линия изокосты станет более пологой.

Изобразим на одном рисунке несколько изокост, которые характеризуют разные уровни издержек производства (ТС₁, ТС₂ ,ТС₃), и изокванту, показывающую заданный объем производства. Там, где изокванта касается одной из изокост в точке Е, заданный объем будет произведен при наименьших издержках (рис. 17.)

Рис. 17. Минимизация издержек при заданном объеме продукции.

Точка Е – точка равновесия производителя. В этой точке соотношение предельных продуктов труда и капитала равно соотношению их цен:

или

Если задана величина издержек и требуется в пределах заданного бюджета получить максимум продукции, то это достигается в точке Е – точке касания изоксты и изокванты Q₂ (рис.18.).

Рис.18. Максимизация выпуска продукции при заданных издержках производства.

Рассмотрим ситуацию, когда возможны изменения и объемов производства, и величины издержек (рис.19.). Каждая изокванта касается определенной изокосты. В результате получается ряд точек в которых максимизируются различные объемы выпуска при заданной величине издержек, или минимизируются издержки при заданном объеме производства. Если соединить эти точки, получим траекторию развития фирмы. Это предложение фирмы.

Рис. 19. Траектория развития фирмы.