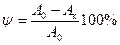|
|
Определение напряжений при растяжении и сжатии.Т.к. при растяжении и сжатии возникает одно внутреннее усилие, то для определения напряжений используют интегральное уравнение (2)
Формула (8) может быть использована, если выполняется гипотеза плоских сечений. Для проверки выполнимости этой гипотезы рассмотрим растяжение образца произвольного сечения с нанесенной на него сеткой. Из уравнения (8) нельзя определить величину σ, так как закон распределения последних в точках поперечного сечения не известен.
Рисунок 4.2 – Исходное состояние
Рисунок 4.3 – При растяжении
При наблюдении деформации растяжения стержня, на поверхности которого нанесены линии, перпендикулярные к оси бруса (рисунок 4.3), можно отметить, что эти линии, смещаясь параллельно самим себе, остаются прямыми и перпендикулярными к оси бруса. Предполагая, что указанная картина перемещения сечений имеет место и внутри стержня, приходим к гипотезе плоских сечений: поперечные сечения стержня, плоские до деформации, остаются плоскими и после нее, перемещаясь поступательно вдоль оси стержня. Разобьем теперь стержень на продольные (параллельные оси стержня) элементы бесконечно малых поперечных сечений и будем в дальнейшем называть их волокнами. На основании гипотезы плоских сечений следует заключить, что все волокна удлиняются на одну и ту же величину Деформация (удлинение) называется упругой, если она исчезает при снятии нагрузки и в этом случае выполняется пропорциональная зависимость между напряжением и относительной деформацией, которая записывается в виде закона Гука:
Здесь: σ – нормальное напряжение; Е – модуль упругости – величина постоянная для данного материала, определяется из справочников.
Напряжение – это величина внутреннего усилия, приходящаяся на единицу площади поперечного сечения. Знак напряжения зависит от знака продольной силы в рассматриваемом сечении. В случае сжатия напряжения считают отрицательным. Отметим, что формула (10) справедлива лишь для сечений, достаточно удаленных от мест приложения сосредоточенных нагрузок. Вблизи приложения нагрузок распределение напряжений носит сложный характер и требует более точных методов исследования. Определяя напряжения при растяжении, сжатии и при других видах деформаций, в сопротивлении материалов, а также в теории упругости широко пользуются следующим весьма важным положением, носящим название принципа Сен-Венана: если тело нагружается статически эквивалентными системами сил, т.е. такими, у которых главный вектор и главный момент одинаковы, и при этом размеры области приложения нагрузок невелики по сравнению с размерами тела, то в сечениях, достаточно удаленных от мест приложения сил, напряжения мало зависят от способа нагружения. Общего теоретического доказательства принцип Сен-Венана не имеет, но его справедливость подтверждается многочисленными теоретическими и экспериментальными исследованиями.
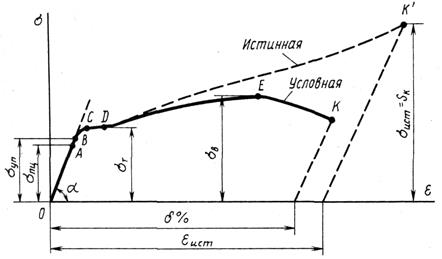
2.7 Испытания на растяжение Наибольшую информацию о механических свойствах металлов получают из статических испытаний на растяжение. На испытательных машинах получают графическое представление зависимости между действующей силой F и удлинением Dl, называемое диаграммой растяжения или сжатия образца. На рис. 1.12 представлена диаграмма растяжения образца из низкоуглеродистой стали. Чтобы получить механические характеристики материала, из которого изготовлен образец, надо исключить влияние конкретных размеров и формы образца. С этой целью усилия F относят к первоначальной площади поперечного сечения A0, а абсолютное удлинение Dl - к первоначальной длине образца l0. Получается диаграмма условных напряжений σ=f(ε), которая имеет тот же вид, что и диаграмма F=f(Dl), т. к. A0 и l0 постоянны. (Рис. 1.13). На участке OA выполняется закон Гука. Точка A соответствует пределу пропорциональости:
Пределом пропорциональности σпц называется наибольшее напряжение, до которого существует прямо пропорциональная зависимость между нагрузкой и деформацией. Для стали марки Ст3 предел пропорциональности приблизительно равен σпц =195…200 МПа. На прямолинейном участке диаграммы определяют модуль упругости
Рисунок 1.12
Рисунок 1.13
Пределом упругости σуп называется максимальное напряжение, при котором в материале не обнаруживается признаков пластической (остаточной) деформации. Для Ст3 σуп =205…210 МПа. CD – площадка текучести. Здесь деформации растут практически без увеличения нагрузки, т. к. идёт процесс распространения пластических деформаций по длине рабочей части образца. Физическим пределом текучести
называется наименьшее напряжение, при котором образец деформируется без заметного увеличения растягивающей нагрузки. Для Ст3 σТ =220…250 МПа. Напряжение σТ часто используется в качестве предельного в расчётах на прочность пластичных материалов. Пластические деформации вызывают изменение внутренней структуры металла, что приводит к его упрочнению. Образец приобретает способность воспринимать возрастающее усилие до значения Fmax – точка Е на диаграмме. Усилие Fmax используется для вычисления временного сопротивления, называемого также пределом прочности:
Напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению образца, называется временным сопротивлением. Для Ст3 временное сопротивление σВ=370…470 МПа. Зона DE называется зоной упрочнения. При максимальном усилии или несколько меньшем его на образце в наиболее слабом месте возникает локальное уменьшение поперечного сечения – шейка. Дальнейшая деформация происходит в этой зоне образца. В точке K образец разрушается. Истинное сопротивление разрыву
где АK – площадь поперечного сечения в месте разрыва. Зона EK называется зоной местной текучести. Истинные напряжения в момент разрыва (в шейке) в образце из стали Ст3 достигают 900…1000 МПа. Чтобы определять истинные напряжения в каждый момент нагружения, необходимо силу делить на текущее значение площади поперечного сечения. Следовательно, истинные напряжения больше условных. Истинная деформация малого участка образца с начальной длиной x0
где x – текущая длина выделенного участка образца. Пластичность материала оценивают: 1) величиной относительного остаточного удлинения при разрыве, определяемой в процентах 2) величиной относительного остаточного уменьшения площади начального сечения образца при разрыве
|
|

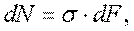

 и их относительные удлинения ε одинаковы.
и их относительные удлинения ε одинаковы.
 - относительная деформация
- относительная деформация
 , значит σ можно вынести за знак интеграла (8).
, значит σ можно вынести за знак интеграла (8).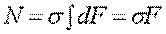

 . (1.22)
. (1.22) , который характеризует жёсткость материала при упругих деформациях.
, который характеризует жёсткость материала при упругих деформациях.  – масштабные коэффициенты.
– масштабные коэффициенты.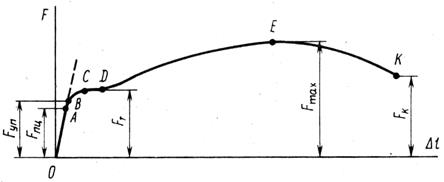
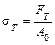 (1.23)
(1.23) . (1.24)
. (1.24) , (1.25)
, (1.25) , (1.26)
, (1.26) , где lк – конечная длина расчётной части образца (после разрыва)
, где lк – конечная длина расчётной части образца (после разрыва)