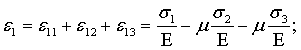|
|
Главные напряжения. Виды напряженного состояния.При изменении ориентации граней выделенного элемента меняются также действующие на его гранях напряжения. При этом можно провести такие площадки, на которых касательные напряжения равны нулю. Площадки, на которых касательные напряжений нет, называются главными площадками, а нормальные напряжения на этих площадках – главными напряжениями. Как бы ни было загружено тело, в каждой точке его имеются, по крайней мере, три главные площадки, причем они взаимно перпендикулярны. Следовательно, в каждой точке могут действовать и три главных напряжения и они тоже взаимно перпендикулярны. Направления, параллельные главным напряжениям, называются главными направлениями напряжений или главными осями в данной точке. Главные напряжения условимся обозначать σ1, σ2 и σ3; при этом индексы следует расставлять так, чтобы выполнялось неравенство Понимать это неравенство следует в алгебраическом смысле. Поэтому, если, например, одно из главных напряжений равно нулю, другое (растягивающее) составляет 60 МПа, третье (сжимающее) равно -140 МПа, то их обозначают так: Таким образом, в точках нагруженного тела можно выделить элементарные параллелепипеды, на гранях которых действуют только нормальные – главные напряжения.
Виды напряженного состояния: 1) линейное напряженное состояние – когда на элементарный параллелепипед действует одно главное напряжение (растяжение или сжатие) (рисунок 7.4)
Рисунок 7.4 – Линейное напряжённое состояние
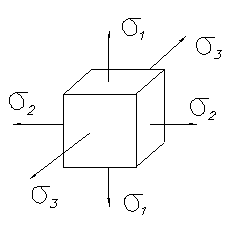
Рисунок 7.5 – Плоское напряжённое сотояние
2) Плоское напряженное состояние – когда на элементарный параллелепипед действует 2 главных напряжения (рисунок 7.5).
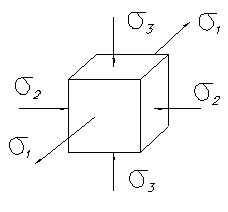
3) Объемное напряженное состояние – когда на элементарный параллелепипед действует все три главных напряжения:
Рисунок 7.7 – Объёмное напряжённое состояние
Кроме того, различают однородные и неоднородные напряженные состояния. В однородном напряженном состоянии напряжения одинаковы в каждой точке какого – либо сечения и всех параллельных ему сечений. В случае однородного напряженного состояния размеры выделенных элементов не играют никакой роли, так как напряжения одинаковы во всех точках одной (любой) грани и, следовательно, равномерно распределены по каждой грани. В неоднородном напряженном состоянии элемент следует полагать бесконечно малым. Тогда предположение о равномерном распределении напряжений по его граням выполняется с точностью до малых второго порядка. Следовательно, независимо от того, однородное или неоднородное напряженное состояние будет во всем теле, выделенные элементы рассматриваем пребывающими в однородном напряженном состоянии. При расчете элементов конструкций на прочность определяют экстремальные значения нормальных и касательных напряжений в точках нагруженного тела, а также положения площадок, на которые они действуют. Решая такую задачу, полагают, что напряжения на гранях параллелепипеда, выделенного в точке, известны и требуется найти напряжения на любых площадках, проведенных в окрестности точки. Она легко решается из рассмотрения равновесия части параллелепипеда, отсеченной данной площадкой. Наиболее просто решить поставленную задачу, если первоначальный элемент выделен главными площадками, а исходными являются главные напряжения.
Обобщенный закон Гука. При растяжении-сжатии закон Гука имел следующий вид: μ – коэффициент Пуассона Рассмотрим объемное напряженное состояние в случае всестороннего растяжения (рисунок 7.8)
Рисунок 7.8 – Расчётная схема
Используя принцип независимости действия сил, рассмотрим действие каждого σ отдельно, а результат сложим: i – указывает на то, какому напряжению параллельна данная ε j – указывает на причину данной деформации, т.е. напряжение, которое вызвало данное ε. Приведенные формулы выражают обобщенный закон Гука для изотропного тела, т.е. зависимость между линейными деформациями и главными напряжениями в общем случае трехосного напряженного состояния. Заметим, что сжимающие напряжения подставляют в эти формулы со знаком «минус».
|
|


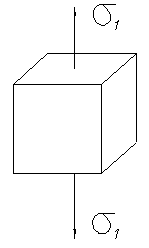
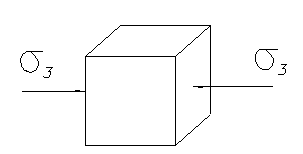
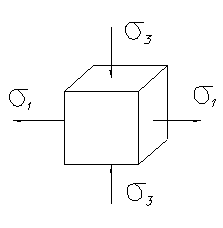
 Рисунок 7.6 - Пример
Рисунок 7.6 - Пример