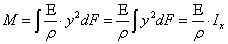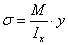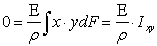|
|
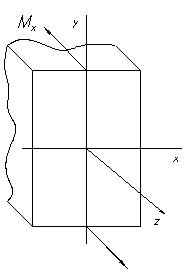
Определение напряжений при чистом изгибе.Проведем поперечное сечение на произвольном расстоянии от начала координат (рис. 6.1). В плоскости сечения проведем координатные оси у, х и z: ось у совместима с силовой линией (линией пересечения силовой плоскости с плоскостью сечения), а ось х проведем на произвольной пока высоте, но перпендикулярно к оси у. Ось z направим перпендикулярно к плоскости сечения.
Рисунок 8.1
Т.к. при чистом изгибе возникает только момент Мх, то в данном сечении могут возникнуть только нормальные напряжения, поэтому из шести интегральных уравнений равновесия выпишем те, которые содержат σ. (см. пункт 3.1 формулы (2), (5), (6)).
Т.к. N = 0, My = 0, Mx = M при чистом изгибе, то:
Интегралы 7 – 9 могут быть использованы, если выполняется гипотеза плоских сечений, поэтому рассмотрим балку с нанесенной на нее сеткой. а)
б) Рисунок 8.2 – Гипотеза плоских сечений
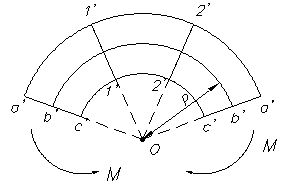
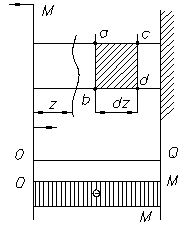
При изгибе верхние волокна «а» находятся в зоне растяжения, а волокна «с» - в зоне сжатия. Между зоной растяжений и сжатия обязательно существует волокно, которое не испытывает ни того, ни другого. Совокупность волокон, не меняющих своей длины при изгибе балки, называется нейтральным слоем. Волокна, принадлежащие нейтральному слою, до деформации лежат в одной плоскости, а в деформированном состоянии образуют некоторую цилиндрическую поверхность. В обоих случаях каждое поперечное сечение пересекается с нейтральным слоем по прямой, которая называется нейтральной линией сечения. При плоском изгибе нейтральный слой оказывается перпендикулярным к силовой плоскости, а значит, нейтральная линия перпендикулярна к силовой линии в сечении. Будем считать, что ось х проведена в сечении так, что она совпадает с нейтральной линией (но положение последней по высоте сечения пока неизвестно). ρ – радиус кривизны нейтрального слоя Рассмотрим балку в состоянии чистого изгиба. Двумя сечениями ab и cd вырежем элементарный элемент длиной dz (рис. 8.3 б)
а)
б) Рисунок 8.3 – Чистый изгиб
Рассмотрим выделенный элемент abcd (рис. 8.3 а). Пусть сечение ab условно неподвижно, а сечение cd повернется относительно ab на некоторый угол dθ. При этом cd займет положение
Подставим (10) в закон Гука при растяжении:
Подставим (11) в интеграл (8), следовательно:
(13) – формула кривизны нейтрального слоя. Подставим (13) в (11):
где М – внутренний изгибающий момент, который берется из эпюры М. Ix – осевой момент инерции относительно нейтральной оси сечения. у – расстояние от оси х до точки, в которой находится σ. Выясним, какое место занимает х в произвольном сечении, для этого подставим (11) в (7) и (9): поэтому ось х является центральной. значит ось х является главной осью Ось х является главной центральной осью любого сечения. Таким образом, если силовая линия совпадает с одной из главных центральных осей сечения, то изгиб будет плоским и нейтральная линия сечения совпадает с другой главной центральной осью. Иначе говоря, если силовая плоскость совпадает с одной из главных плоскостей стержня, то нейтральный слой совпадает с другой главной плоскостью. Формула (13) в проведенном выводе была вспомогательной, однако она имеет и большое самостоятельное значение. Её можно трактовать как закон Гука при изгибе, поскольку она связывает деформацию (кривизну нейтрального слоя l/ρ) с действующим в сечении моментом. Произведение EJ носит название жесткости сечения при изгибе, Н*м2. Из формулы (13) видно, что если балка изготовлена из однородного материала (E = const) и имеет постоянное сечение (J = const), то при чистом изгибе (М = const) ось ее искривляется по дуге окружности (l/ρ = const, и, значит, ρ = const).
|
|
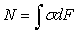





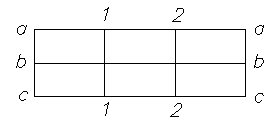
 . Вертикальные сечения 1-1, 2-2 остаются плоскими, но поворачиваются относительно друг друга на некоторый угол, поэтому можно пользоваться формулами (7) - (9), т.к. гипотеза плоских сечений выполняется.
. Вертикальные сечения 1-1, 2-2 остаются плоскими, но поворачиваются относительно друг друга на некоторый угол, поэтому можно пользоваться формулами (7) - (9), т.к. гипотеза плоских сечений выполняется.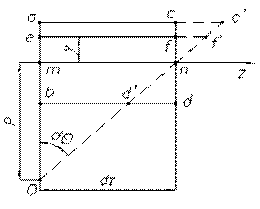
 . mn – нейтральный слой с радиусом ρ. Выделим произвольное волокно ef на расстоянии у от оси z и найдем его относительную деформацию:
. mn – нейтральный слой с радиусом ρ. Выделим произвольное волокно ef на расстоянии у от оси z и найдем его относительную деформацию: