|
|
Внутренние силовые факторы (метод сечений)
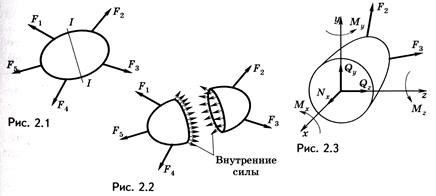
Пусть свободное тело под действием системы известных внешних сил F1—F5 находится в равновесии (рис. 1.1). Требуется определить внутренние силы в сечении I—I. Мысленно разрежем тело на две части по данному сечению. Обе части после разреза, вообще говоря, не будут находиться в равновесии, так как нарушены внутренние связи. Заменим действие левой части тела на правую и правой на левую некоторой системой сил в сечении I—I, т. е. внутренними силами (рис. 2.2). Характер распределения внутренних сил в сечении неизвестен, но они должны обеспечить равновесие каждой части тела. Мысленно отбросим одну из частей. Для составления условия равновесия оставленной части приведем внутренние силы в виде главного вектора и главного момента к центру тяжести сечения и спроецируем их на оси координат (рис. 2.3). Получим три проекции главного вектора Nx, Qy, Qz и три проекции главного момента Мх, Мy, Мz, которые называются внутренними силовыми факторами: Nx — продольная сила; Qy, Qz — поперечные силы; МК(Мx) — крутящий момент, Мz, Мy — изгибающие моменты.
Условия равновесия оставленной части
где
Проекции сил и моменты в уравнения равновесия подставляют со знаками «+», если они совпадают с предварительно выбранным положительным направлением, и «-» - если имеют противоположное направление. Направление (и, следовательно, знак) неизвестных внутренних силовых факторов предварительно принимают произвольно. Если внешние нагрузки известны, то с помощью уравнений равновесия можно определить внутренние силовые факторы
Если в результате решения уравнения равновесия внутренний силовой фактор получился со знаком «+», то его направление было угадано верно; если со знаком «-», то действительное направление противоположно тому, что было принято вначале, и следует поменять направление стрелочки на схеме. Основные виды деформаций
Рисунок 2.4 Различают следующие основные виды деформаций: растяжение-сжатие (рис. 2.4, а, б, Nx ≠ 0); сдвиг (рис. 2.4, в, Q ≠ 0); кручение (рис. 2.4, г, Мк ≠ 0); изгиб (рис. 2.4, д, МИЗГ ≠ 0).
Понятие о напряжении
Из гипотезы о сплошности материала следует, что внутренние силы непрерывно распределены по площади поперечного сечения тела. Пусть на малую, но конечную площадку DА (рис. 1.5) действует внутренняя элементарная сила DR. Разложив DR на составляющие по осям х, у, z, получим ее компоненты DNx, DQy, DQz. Отношение вида pср = DR/DА (1.12) определяет среднее полное напряжение на данной площадке DА. Полное напряжение в точке есть отношение p= lim DR/DА или DА®0 которое определяет интенсивность внутренних сил в данной точке рассматриваемого сечения. Поскольку через точку тела можно провести бесчисленное множество сечений, то в данной точке имеется бесчисленное множество напряжений, связанных с площадками действия. Совокупность всех напряжений, действующих на разных площадках в данной точке, называется напряженным состоянием точки. Единица напряжения — Н/м2, или Па (Паскаль). По аналогии с (1.13) можно записать:
Выражение (1.14) определяет нормальное напряжение σх (рис. 1.6), вектор которого направлен так же, как и вектор нормальной силы Nx. Выражения (1.15) и (1.16) определяют касательные напряжения τ; их векторы имеют те же направления, что и, соответственно, DQy и DQz. Первый индекс при τ указывает, какой оси параллельна нормаль к площадке действия рассматриваемого напряжения, второй индекс показывает, какой оси параллельно данное напряжение. Зависимость между полным напряжением p и его составляющими выражается формулой
2.4 Деформация
Реальные тела под воздействием внешних сил могут изменять свою форму и размеры – деформироваться. Определение величины этих изменений называется расчётом на жёсткость. Все возможные изменения формы можно оценить, используя всего лишь два вида деформаций: линейные (рис. 1.7) и угловые (рис. 1.8). |
|
 ;
;  ;
; ;
; 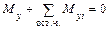 ;
; ;
;  ; (1.10)
; (1.10) ,
,  ,
,  ,
, 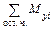 ,
,  - суммы моментов всех внешних сил, действующих на оставленную часть тела, относительно соответствующих осей координат.
- суммы моментов всех внешних сил, действующих на оставленную часть тела, относительно соответствующих осей координат. ;
; 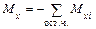 ;
; ;
; 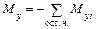 ;
; ;
;  . (1.11)
. (1.11)
 , (1.13)
, (1.13) или
или  , (1.14)
, (1.14) или
или  , (1.15)
, (1.15)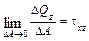 или
или  . (1.16)
. (1.16) Рисунок 1.5
Рисунок 1.5
 Рисунок 1.6
Рисунок 1.6
 . (1.17)
. (1.17)