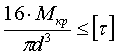|
|
Определение касательных напряжений при кручении вала круглого поперечного сечения.Из пункта 3.1 выпишем интегральное уравнение равновесия (8): Т.к. при кручении действует суммарный τ, то последнее выражение запишем в другом виде:
Выясним, выполняется ли гипотеза плоских сечений, при кручении и можно ли пользоваться интегралом (4): на поверхности круглого вала нанесем сетку, состоящую из линий, параллельных оси, и линий, представляющих собой параллельные круги (рис. 5.3). После приложения скручивающего момента наблюдаем следующее: образующие цилиндра превращаются в винтовые линии, т.е. лини одинакового наклона к оси стержня, параллельные круги не искривляются и расстояние между ними практически остается неизменным; радиусы, проведенные в торцовых сечениях, остаются прямыми. Полагая, что картина, наблюдаемая на поверхности стержня, сохраняется и внутри, приходим к гипотезе плоских сечений: сечения, плоские до деформации, остаются плоскими при кручении круглого стержня, поворачиваясь одно относительно другого на некоторый угол закручивания.
Рисунок 6.3 – Гипотеза плоских сечений Рассмотрим произвольный вал, нагруженный
Рассмотрим этот элемент (рис. 6.4, б), принимая, что сечение 1-1 условно неподвижно, а 2-2 относительно 1-1 повернется на некоторый угол dφ. Выделим произвольное волокно С1С2 на расстоянии ρ от оси z. При кручении точка С2 переместится в точку Используя (2), находим, что По аналогии с формулой (3):
Из формулы (1)
Приравняем правые части (5) и (6):
Подставим (7) в (4):
Используя формулу (3):
Подставим (8) в (7):
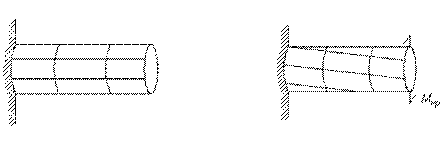
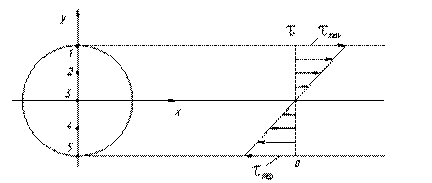
Здесь: Мкр – внутренний крутящий момент, берется из эпюры кручения Ip – полярный момент инерции. ρ – расстояние от оси z до точки (до волокна), в котором находится данное τ. 6.3 Закон распределения τ по высоте круглого сечения. Из анализа общей формулы (10) для касательных напряжений видно, что напряжения в плоскости сечения вала распределены неравномерно и в зависимости от радиуса изменяются по линейному закону от нуля в центре сечения до максимума на его периферии (рис. 5.5). В продольных сечениях, проходящих через ось вала, по закону парности касательных напряжений возникают такие же по величине касательные напряжения. В элементе материала, мысленно выделенном из наружных слоев стержня сечениями, параллельными и перпендикулярными к образующим, по граням будут действовать только касательные напряжения. В сечениях, наклонных к оси, будут также и нормальные напряжения. Наибольшие нормальные напряжения действуют на главных площадках, которые, как известно, наклонены под углом 45º к площадкам сдвига (при кручении – под углом 45º к оси вала). Таким образом, при кручении круглых валов опасными могут стать как касательные напряжения, возникающие в поперечных и в продольных сечениях вала, так и нормальные напряжения, возникающие в площадках под углом 45º к первым. В связи с этим характер разрушения вала будет зависеть от способности материала сопротивляться действию касательных и нормальных напряжений. Так, если материал сопротивляется касательным напряжениям, то первые трещины разрушения возникают по образующим в местах действия наибольших касательных напряжениях. Например, в случае кручения деревянных валов с продольным расположением волокон трещины разрушения ориентированы вдоль образующей, поскольку древесина плохо сопротивляется действию касательных напряжений вдоль волокон. Если же материал плохо сопротивляется растягивающим напряжениям, как например чугун, то трещины разрушения при кручении пройдут по линиям, нормальным к действию главных растягивающих напряжений, т.е. по винтовым линиям, касательные к которым образуют угол 45º с осью стержня. Стальные валы на практике часто разрушаются по поперечному сечению, перпендикулярному к оси вала. Этот вид разрушения обусловлен действием в поперечном сечении касательных напряжений. Рассмотрим круглое поперечное сечение и определим τ в выделенных точках с помощью формулы (10).
Рисунок 6.5 – Закон распределения касательных напряжений
Т.к. Мкр и Ip величины постоянные для всех точек сечения, то τ пропорционально ρ и закон распределения τ – прямая линия, проходящая через 0 в точке 3.
(11) – условие прочности при кручении Wp – полярный момент сопротивления. Для проектирования можно рекомендовать следующий порядок расчета валов на прочность и жесткость при кручении. По схеме вала и действующим на него скручивающим моментам строят эпюру крутящих моментов по отдельным участкам. Выбирают материал для рассчитываемого вала и определяют для этого материала допускаемое напряжение. Записывают условие прочности для участка вала с максимальным значением крутящего момента (согласно эпюре моментов). Если вал достаточно длинный и по отдельным его участкам действуют существенно разные по величине крутящие моменты, то его следует конструировать ступенчатым. Диаметр вала каждой ступени рассчитывают, исходя из той же формулы, но значения крутящего момента при этом берут разные для разных участков в соответствии с эпюрой крутящих моментов. Учитывая, что для сплошного круглого вала
|
|

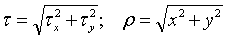

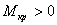 (рис. 6.4, а) Двумя сечениями 1-1 и 2-2 вырежем элементарный момент dz.
(рис. 6.4, а) Двумя сечениями 1-1 и 2-2 вырежем элементарный момент dz.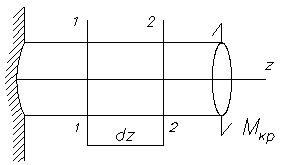
 Рисунок 6.4 – Кручение
Рисунок 6.4 – Кручение и из сектора
и из сектора  найдем:
найдем:
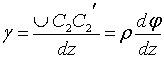



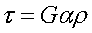

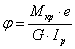

 - касательное напряжение при кручении
- касательное напряжение при кручении


 , можно из выражения (11) записать расчетную формулу для диаметров вала.
, можно из выражения (11) записать расчетную формулу для диаметров вала.