|
|
Произвольная плоская система силМомент силы относительно точки (как скалярная величина)
Силы могут не только придавать ускорение материальной точке или твёрдому телу в его поступательном движении, растягивать или сжимать деформируемое твёрдое тело. Под действием сил, кроме того, твёрдое тело может с ускорением вращаться, а деформируемое твёрдое тело может испытывать деформации кручения или изгиба. Для этого силы должны воздействовать на тело так, чтобы создать момент силы или пары сил. Моментом силы относительно некоторой точки О называется скалярная величина, равная произведению модуля силы на ее плечо относительно этой точки. Знак момента силы принимается условно в зависимости от направления вращения вокруг точки О, которое придаёт сила твёрдому телу.
Единица измерения момента силы – Ньютон умноженный на метр (Н·м).
Для определения момента силы относительно точки рекомендуется придерживаться следующего порядка: 1. Прежде всего, нужно научиться «видеть» силу, момент которой определяем, и центр моментов – точку, относительно которой определяем момент (рис. 1.8 – сила 2. Проводим линию действия силы CD, продлевая вектор силы в обе стороны «до бесконечности». 3. Из центра момента O опускаем перпендикуляр на линию действия силы CD. Длина перпендикуляра h=|OB| от центра момента до линии действия силы и есть плечо. 4. Находим знак момента. Если сила стремится повернуть плечо вокруг центра момента против хода часовой стрелки, то считаем момент положительным; если по ходу часовой стрелки, то отрицательным. 5. Находим числовое значение момента силы относительно точки, умножив модуль силы на плечо. Для примера, который представлен на рисунке,
Cвойства момента силы относительно точки: 1. Момент силы относительно точки не изменится при переносе точки приложения силы вдоль ее линии действия, так как при этом не изменяется ни модуль силы, ни длина ее плеча. 2. Момент силы относительно точки равен нулю только тогда, когда модуль силы равен нулю или когда линия действия силы проходит через точку, так как в этом последнем случае длина плеча равна нулю Теорема Вариньона о моменте равнодействующей: момент равнодействующей плоской системы сходящихся сил относительно некоторой точки, лежащей в плоскости сил, равен алгебраической сумме моментов слагаемых сил относительно той же точки. Пара сил. Момент пары Cистема двух равных по модулю параллельных друг другу и направленных в разные стороны сил Плоскость, в которой расположена пара сил, называется плоскостью действия пары. Кратчайшее расстояние между линиями действия сил пары Пара сил не имеет равнодействующей, т.е. ее нельзя заменить одной силой, ей эквивалентной. Поэтому пара сил не может быть уравновешена одной силой. Вместе с тем силы, составляющие пару сил, не находятся в равновесии. Вращательное действие пары на тело будет тем больше, чем больше плечо пары и модули сил, образующих эту пару, и измеряется так называемым моментом пары. При этом численное значение момента пары определяется как произведение модуля одной из сил пары на плечо этой пары. Алгебраическим моментом пары называется скалярная величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо. Будем обозначать момент пары символом m или m
Рисунок 1.10 – Пары сил
Очевидно, что момент пары равен моменту одной из ее сил относительно точки приложения другой. Понятие момента пары не следует смешивать с моментом силы. Понятие момента силы связано с точкой, относительно которой берется этот момент. Момент пары ни с какой точкой плоскости не связан. Теорема: Действие пары на тело не изменится, если эту пару заменить любой другой парой, лежащей в той же плоскости и имеющей тот же момент. Из данной теоремы вытекают следующие свойства пары сил: 1. Действие пары на тело не изменяется, если переместить пару в другое положение в плоскости ее действия. (Заметим, что перенос пары в ее плоскости действия, так же как и перенос точки приложения силы вдоль линии ее действия, безоговорочно применим только для абсолютно твердого тела). 2. Действие пары на тело не изменится, если одновременно изменить модуль сил пары и величину ее плеча, сохраняя при этом численное значение и знак момента пары. Всякую систему пар, расположенных в одной плоскости, можно заменить одной равнодействующей парой, момент которой равен алгебраической сумме моментов всех пар этой системы. Для равновесия системы пар, расположенных в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма моментов всех данных пар равнялась нулю, т. е. |
|
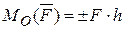

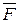 относительно точки O
относительно точки O
 .
. и
и  , линии действия которых не совпадают (рисунок 1.10), образует так называемую пару сил, или просто пару, для обозначения которой будем пользоваться символом
, линии действия которых не совпадают (рисунок 1.10), образует так называемую пару сил, или просто пару, для обозначения которой будем пользоваться символом  .
. .
.
