|
|
Сложение, вычитание, умножение и деление комплексных чисел.Множества. Операции над множествами. Алгебра множеств. Множества с заданными на них операциями. Алгебраические структуры: группа, кольцо, поле. Поле комплексных чисел. Множество - это совокупность, набор элементов, объединенных общими свойствами. Множества обозначаются заглавными латинскими буквами Количество элементов конечного множества называется его мощностью. Мощность множества А обозначается как |A|. Мощность множества — это обобщение понятия количества (числа элементов множества), которое имеет смысл для всех множеств, включая бесконечные. Существуют бо́льшие, есть ме́ньшие бесконечные множества, среди них счётное множество является самым маленьким. Множества, состоящие из конечного числа элементов, называются конечными множествами. Если же число элементов множества неограниченно, то такое множество называется бесконечным. Например, множество всех натуральных чисел бесконечно. Основные операции: 1. Принадлежность и непринадлежность элемента множеству: 2. Объединение множеств: Объединением двух множеств 3. Пересечение множеств: Пересечением двух множеств 4. Разность множеств: Разностью двух множеств
5. Дополнение множества: Если множество
6. Вхождение одного множества в другое множество: Если любой элемент множества 7. Не вхождение одного множества в другое множество: Пусть
1. 2. 3. Объединением множеств 4. а) Коммутативность: для любых множеств A и B верны равенства: АВ=ВА; АВ=ВА. б) Ассоциативность: для любых множеств А, В, С верны равенства: (АВ)С=A(ВС); (AB)С=A(ВС). в) Дистрибутивность: для любых множеств А, B и С справедливы равенства: A(BC)=(AB)(AC); A(BC)=(AB)(AC). Разностью множеств 4. Дополнением множества
Группа, кольцо, поле. 1.Множество 1)операция 2)в 3)для каждого элемента 2.Множество 1) относительно операции сложения множество а) операция сложения коммутативна: б) операция сложения ассоциативна: в) существует нулевой элемент г) для каждого элемента 2) операция умножения в множестве 3) операции сложения и умножения связаны законами дистрибутивности: Если операция умножения коммутативна: Кольцами являются множества целых, рациональных, действительных чисел, причем все они — коммутативные кольца с единицей. Как видим, кольцо— это множество, в котором определены три операции: сложение, умножение и вычитание. 3.Множество 1) 2) для каждого элемента Поле — это множество, в котором определены четыре операции: сложение, умножение, вычитание и деление. Полями, например, являются множества рациональных и действительных чисел. Поле комплексных чисел. Комплексным числомназывается упорядоченная пара вещественных чисел Два комплексных числа Множество всех комплексных чисел обозначается
Пусть Если Если Мнимая единица i — обычно комплексное число, квадрат которого равен отрицательной единице.
и т.д. Аксиомы: 1. 2. 3. 4. 5. Все указанные равенства должны выполняться для произвольных чисел
Сложение, вычитание, умножение и деление комплексных чисел. 1) Сложитьдва комплексных числа Чтобы сложить два комплексных числа, нужно сложить их действительные и мнимые части: 2) Найти разности комплексных чисел Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:
3) Найти произведение комплексных чисел Произведение следует записать так: Помня, что
4) Даны комплексные числа Составим частное: Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение:
Геометрическая интерпретация:
позволяет дать интерпретацию комплексного числа как вектора на плоскости. Сама эта плоскость называется комплексной плоскостью, ось абсцисс на ней — вещественной осью, ось ординат мнимой осью. Тригонометрическая интерпретация: Для числа
при этом корень квадратный в правой части понимается как корень арифметический, т.е. как единственное неотрицательное вещественное число, квадрат которого равен Аргументом комплексного числа
которые позволяют однозначно восстановить5) угол в интервале Итак, комплексное число
Последняя называется тригонометрической формой комплексного числа.
Формула Муавра Если комплексное число нужно возвести в n-ую степень, на помощь приходит формула Муавра: если комплексное число представлено в тригонометрической форме
Справедливо неравенство треугольника:
Корень n-степени из комплексного числа: Уравнение вида |
|
 , а элементы множества строчными латинскими буквами
, а элементы множества строчными латинскими буквами 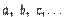 .
. ,
, 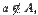
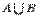 .
. и
и  называется множество
называется множество  , состоящее из элементов множеств
, состоящее из элементов множеств  и
и  , т.е.
, т.е.  или
или 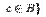
 .
. и
и  называется множество
называется множество  , состоящее из общих элементов множеств
, состоящее из общих элементов множеств  и
и  и
и 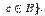
 .
. и
и  называется множество
называется множество 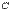 , состоящее из элементов множества
, состоящее из элементов множества  , т.е.
, т.е. и
и 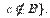
 .
. , тогда определяется операция дополнения:
, тогда определяется операция дополнения: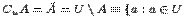 и
и 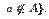
 .
. является элементом множества
является элементом множества  , то говорят, что множество
, то говорят, что множество  .
. и
и  — произвольные множества.
— произвольные множества.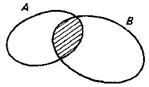 Под универсумом
Под универсумом  понимают множество, включающее в себя все множества в данном контексте.
понимают множество, включающее в себя все множества в данном контексте. Пересечением множеств
Пересечением множеств  и
и  называется множество всех таких элементов
называется множество всех таких элементов  , которые лежат как в множестве
, которые лежат как в множестве 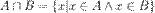 .
. и
и  , то есть
, то есть  .
. Свойства операций объединения и пересечения.
Свойства операций объединения и пересечения.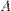 и
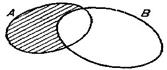
и  называется множество всех таких элементов
называется множество всех таких элементов 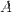 , но не лежат в
, но не лежат в  .
. называется множество всех таких элементов
называется множество всех таких элементов  .
.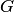 с алгебраической операцией
с алгебраической операцией  называется группой, если выполняются следующие условия:
называется группой, если выполняются следующие условия: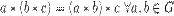 ;
; ;
;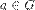 существует обратный ему элемент
существует обратный ему элемент  . Если операция
. Если операция  , на котором заданы две операции — сложение
, на котором заданы две операции — сложение  и умножение
и умножение 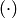 , называется кольцом, если выполняются следующие условия:
, называется кольцом, если выполняются следующие условия: ;
; ;
; ;
; существует противоположный ему элемент
существует противоположный ему элемент  ;
;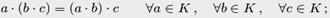
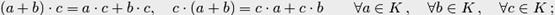
 , то кольцо называется коммутативным, в противном случае кольцо называется некоммутативным. Если для операции умножения существует единичный элемент
, то кольцо называется коммутативным, в противном случае кольцо называется некоммутативным. Если для операции умножения существует единичный элемент  , то говорят, что кольцо
, то говорят, что кольцо  , на котором заданы две операции: сложение
, на котором заданы две операции: сложение  ;
; , отличного от нулевого
, отличного от нулевого  , существует обратный элемент
, существует обратный элемент  .
. .
.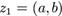 и
и 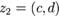 называются равными:
называются равными: 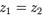 тогда и только тогда, когда
тогда и только тогда, когда  и
и  . В противном случае они называются неравными.
. В противном случае они называются неравными.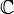 .
. — комплексное число, где
— комплексное число, где  и
и 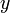 — вещественные числа. Числа
— вещественные числа. Числа  или
или  и
и  или
или  называются соответственно вещественной и мнимой частями
называются соответственно вещественной и мнимой частями  .
. , то
, то  , то
, то 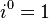
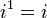
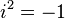
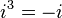
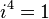
 – коммутативность;
– коммутативность; – ассоциативность;
– ассоциативность; – коммутативность;
– коммутативность; – ассоциативность;
– ассоциативность; – дистрибутивность;
– дистрибутивность; .
. ,
, 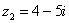
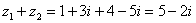
 и
и  , если
, если  ,
, 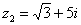
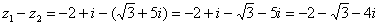
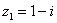 ,
, 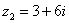
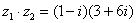
 , считаем знакомыми нам алгебраическими действиями:
, считаем знакомыми нам алгебраическими действиями: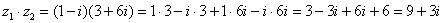
 ,
,  . Найти частное
. Найти частное  .
.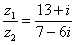
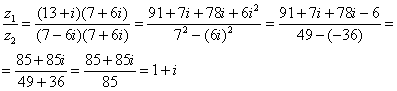
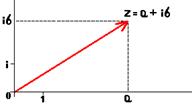 Если на плоскости
Если на плоскости  задана декартова прямоугольная система координат, то задание точки
задана декартова прямоугольная система координат, то задание точки  ее координатами
ее координатами  однозначно определяет вектор, имеющий начало в начале координат
однозначно определяет вектор, имеющий начало в начале координат 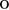 (
( 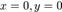 ), а конец — в точке
), а конец — в точке  . Такое соответствие
. Такое соответствие
 его модулем называется неотрицательное вещественное число обозначаемое
его модулем называется неотрицательное вещественное число обозначаемое  , определяемое как
, определяемое как
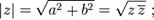
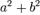 .
. называется величина угла, образованного на комплексной плоскости вектором
называется величина угла, образованного на комплексной плоскости вектором  с вещественной осью. При этом угол будет отсчитываться от вещественной оси в положительном направлении, т.е. против часовой стрелки, и что он будет находиться в интервале
с вещественной осью. При этом угол будет отсчитываться от вещественной оси в положительном направлении, т.е. против часовой стрелки, и что он будет находиться в интервале  если вычисляется в радианах. Аргумент комплексного числа
если вычисляется в радианах. Аргумент комплексного числа  не определяется. Обозначим аргумент числа
не определяется. Обозначим аргумент числа  через
через  . Для определения
. Для определения  мы имеем две формулы:
мы имеем две формулы: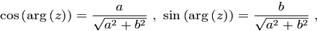
 .
. , наряду со своей нормальной формой
, наряду со своей нормальной формой 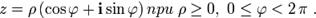
 , то при его возведении в натуральную степень
, то при его возведении в натуральную степень 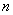 справедлива формула:
справедлива формула: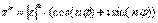
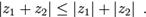
 имеет ровно
имеет ровно  , которые можно найти по формуле:
, которые можно найти по формуле: , где
, где  – это модуль комплексного числа
– это модуль комплексного числа 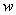 ,
,  – его аргумент, а параметр
– его аргумент, а параметр  принимает значения:
принимает значения: 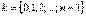 .
.