|
|
СВОЙСТВА СОБСТВЕННЫХ ВЕКТОРОВ И СОБСТВЕННЫХ ЗНАЧЕНИЙ ЛИНЕЙНОГО ОПЕРАТОРАПусть A — линейный оператор, действующий в n-мерном линейном пространстве X, λ i— собственное значение оператора A, а ei — соответствующий собственный вектор: A(ei ) = λ iei, ei ≠ 0, ei ∈X. Или пусть A — матрица оператора A, или произвольная квадратная матрица, λ i— собственное значение матрицы A, а ei — соответствующий собственный вектор: A·ei = λ iei,ei ≠ 0, ei ∈X. — Если λ1, λ2, ..., λn — собственные значения матрицы A, то tr A = a11+ a22+...+ ann = λ1 + λ2 + ...+ λn. — Если λ1, λ2, ..., λn — собственные значения матрицы A, то det A = λ1 · λ2 · ...· λn. — Собственные значения λ i являются корнями характеристического уравнения det(A −λE) = 0. — Оператор A (матрица A) имеет не более n различных собственных значений. — Собственные значения матриц A и AT совпадают. — Если матрица A обратима, то все её собственные значения отличны от нуля, λ i≠ 0; при этом собственными значениями обратной матрицы A− 1 являются числа (λ i)− 1, а соответствующие собственные векторы совпадают. — Если число λ — собственное значение матрицы A, то собственным значением матрицы Ak является число λk , а соответствующие собственные векторы совпадают. — Собственные значения подобных матриц A и C− 1·A·C совпадают. Здесь C — невырожденная матрица. — Собственный вектор, отвечающий собственному значению λ i является ненулевым решением линейной однородной системы (A −λE)· x = 0, x≠ 0, x ∈ X. — Собственные векторы, отвечающие различным собственным значениям, линейно независимы. — Если линейный оператор A имеет n различных собственных значений, то соответствующие собственные векторы образуют базис пространства X, который называется собственным базисом линейного оператора. — Если линейный оператор имеет собственный базис, то матрица оператора в собственном базисе имеет диагональный вид; диагональными элементами являются собственные значения оператора. — Собственные векторы, отвечающие различным собственным значениям, ортогональны.
Предел функций Определение 1. Пусть функция Говорят, что существует конечный предел = b, если для любого, сколь угодно малого числа
Существует второе определение предела: Определение 2. Говорят, что существует предел f(x) = b, при x ->x0, если для любой последовательности xnсоответствующее последующее значение функции ->b. Первое определение по Коши, второе определение по Гейне. Они эквивалентны. Если есть предел по Коши, то есть предел по Гейне (и наоборот).
Билет №17 Пределы последовательностей В математике пределом последовательностиэлементов метрического пространства или топологического пространстваназывают элемент того же пространства, который обладает свойством «притягивать» элементы заданной последовательности. Пределом последовательности элементов топологического пространства является такая точка, каждая окрестность которой содержит все элементы последовательности, начиная с некоторого номера. В метрическом пространстве окрестности определяются через функцию расстояния, поэтому понятие предела формулируется на языке расстояний. Исторически первым было понятие предела числовой последовательности, возникающее в математическом анализе, где оно служит основанием для системы приближений и широко используется при построении дифференциальногои интегрального исчислений. Обозначение (читается: предел последовательности икс-энное при эн, стремящемся к бесконечности, равен a): аитПусть дано топологическое пространство
где Теоремы о пределах Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функцииg(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).
Теорема 3. Предел постоянной равен самой постоянной.
Доказательство. f(x)=с, докажем, что Возьмем произвольное >0. В качестве можно взять любое положительное число. Тогда при
Теорема 4. Функция не может иметь двух различных пределов в одной точке. Доказательство. Предположим противное. Пусть
По теореме о связи предела и бесконечно малой функции: f(x)-A= f(x)-B= Вычитая эти равенства, получим: B-A= Переходя к пределам в обеих частях равенства при B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему. Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при
Доказательство. Пусть Тогда, по теореме о связи предела и б.м. функции:
Сложим алгебраически эти равенства: f(x)+g(x)-h(x)-(А+В-С)= где По теореме о связи предела и б.м. функции:
Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при
Следствие. Постоянный множитель можно выносить за знак предела.
Теорема 7. Если функции f(x) и g(x) имеют предел при причем
|
|
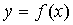 определена в некоторой числовой оси.X0 принадлежитХ или не принадлежит.
определена в некоторой числовой оси.X0 принадлежитХ или не принадлежит. существует число, что как только x-x0 станет меньше б(
существует число, что как только x-x0 станет меньше б( 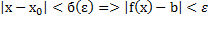
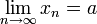
 и последовательность
и последовательность  Тогда, если существует элемент
Тогда, если существует элемент  такой, что
такой, что ,
, — открытое множество, содержащее
— открытое множество, содержащее  , то он называется пределом последовательности
, то он называется пределом последовательности 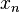 .
.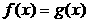
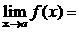
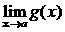 .
.
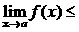
 .
.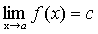 .
.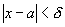
 .
.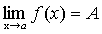 и
и 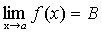 .
.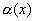 - б.м. при
- б.м. при 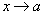 ,
, - б.м. при
- б.м. при 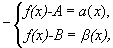
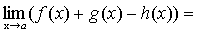
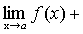

 .
.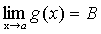 ,
, 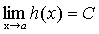 .
. где
где  - б.м. при
- б.м. при 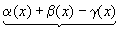 ,
, б.м. при
б.м. при  А+В-С=
А+В-С= 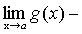
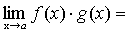
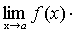
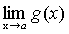 .
.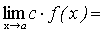
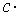
 .
.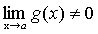 , то и их частное имеет предел при
, то и их частное имеет предел при  ,
,