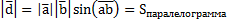|
|
Критерии совместности системы. Теорема о совместности Кронекера-КапеллиТеорема Кронекера-Капелли – критерий совместности системы линейных алгебраических уравнений: Определение
Доказательство Необходимость Пусть система совместна. Тогда существуют числа Достаточность Пусть Метод Гаусса Сущность метода в том, что расширенная матрица системы с помощью элементарных преобразований над ее строками приводится к ступенчатому виду. Далее последовательно находятся все неизвестные, начиная снизу вверх. Метод Гаусса - наиболее универсальный метод для нахождения решения любой системы линейных уравнений, он работает в случае, когда система не являются квадратной, имеет бесконечно много решений или несовместна. Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса, обратный - методом Гаусса-Жордана, который отличается от первого только последовательностью исключения переменных. Линейное пространство. Базис ЛП. Определение базисов ЛП. Размерность ЛП. Разложение по базису. Две теории о проекциях. Определение линейного пространства Непустое множество · Для любых двух элементов 1. Коммутативность: 2. Ассоциативность: 3. Существование нуля: существует такой элемент 4. Существование противоположного элемента: для каждого · Для любого числа 1. 2. 3. 4. В зависимости от того, какие числа используются для построения линейного пространства, различают действительные и комплексные линейные пространства. Можно также рассматривать линейные пространства, построенные над произвольным полем. Элементы линейного пространства часто называют векторами. Базис линейного пространства Упорядоченная система векторов
Размерность линейного пространства Если существует натуральное число n такое, что X содержит линейно независимую систему из n векторов, а любая система из n + 1 вектора линейно зависима, то X называется n –мерным линейным пространством, а число n – его размерностью. Будем обозначать n –мерное линейное пространство Xn , где n — размерность пространства Xn . Из определения следует, что размерность линейного пространства равна максимальному количеству линейно независимых векторов.
Евклидовы пространства. Евклидовым вещественным пространством называют линейное вещественное пространство в котором введена операция скалярного умножения элементов, которая подчиняется следующим аксиомам: x, y,z є L и число a є R 1. (x, y) = (y,x); 2. (x + y,z) = ((x,z) + (y,z)); 3. (ax, y) = (x,ay) = a(x, y); 4. (x,x) > 0 для всех x є L; 5. (x,x) = 0 , если x = 0. x, y – элементы линейного пространства.
1)
 y y

{ī, ῑ}= е- базис
  y y
 

{ī, ῑ, k} = е- базис
n- мерноеЕвклидово пространство
Длина вектора: X є E П1. П2. П3.
О.
Длина суммы 2х сторон не превышает суммы длин этих сторон. Базис
Базис
Основные понятия аналитической геометрии. Векторная алгебра. Скалярное произведение. Векторное произведение. Смешанное произведение. Основные понятия аналитической геометрии. Аналитическая геометрия — раздел геометрии, в котором геометрические фигуры и их свойства исследуются средствами алгебры. Основные понятия геометрии (точки, прямые линии и плоскости) относятся к числу так называемых начальных понятий. Эти понятия можно описать, но всякая попытка дать определение каждого их этих понятий неизбежно сведется к замене определяемого понятия ему эквивалентным. В основе этого метода лежит так называемый метод координат, впервые применённый Декартом. Каждому геометрическому соотношению этот метод ставит в соответствие некоторое уравнение, связывающее координаты фигуры или тела.
Векторная алгебра. Векторная алгебра - раздел векторного исчисления, в к-ром изучаются простейшие операции над (свободными) векторами. К числу этих операций относятся линейные операции над векторами: операция сложения векторов и умножения вектора на число.
Скалярное произведение. Скалярным произведением векторов a и b называется число, равное Если один из векторов нулевой, то угол Скалярное произведение обозначается Для любых векторов a и b выполнены следующие соотношения:
Векторное произведение. Векторным произведением двух векторов называют третий вектор, который обладает свойствами:
Алгебраические свойства векторного произведения:
Результатом векторного произведения является вектор.
Смешанное произведение. Смешанным произведением трёх векторов
Результатом смешанного произведения является число. Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами
|
|
 такие, что
такие, что 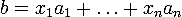 . Следовательно, столбец
. Следовательно, столбец  является линейной комбинацией столбцов
является линейной комбинацией столбцов  матрицы
матрицы  . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что
. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что 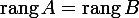 .
. . Возьмем в матрице
. Возьмем в матрице 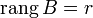 , то он же и будет базисным минором и матрицы
, то он же и будет базисным минором и матрицы  . Тогда, согласно теореме о базисном миноре, последний столбец матрицы
. Тогда, согласно теореме о базисном миноре, последний столбец матрицы  называют линейным пространством (или векторным пространством), если выполняются следующие условия:
называют линейным пространством (или векторным пространством), если выполняются следующие условия: однозначно определён элемент
однозначно определён элемент  , который называется суммой этих элементов и обозначается
, который называется суммой этих элементов и обозначается 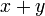 , причём
, причём ,
,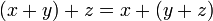 ,
, , что
, что  ,
, существует такой
существует такой 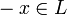 , что
, что  .
.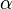 и любого элемента
и любого элемента  (произведение элемента на число), причём
(произведение элемента на число), причём ,
,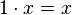 ,
, ,
, .
. называется базисом в X , если
называется базисом в X , если Примеры Евклидовых пространств:
Примеры Евклидовых пространств: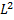


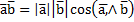
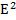 -двумерноеЕвклидово вещественноепространство
-двумерноеЕвклидово вещественноепространство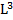



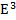 над R
над R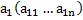
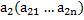
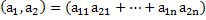
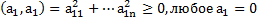
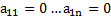
 надR
надR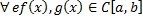
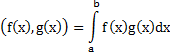
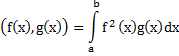
 над R- бесконечномерные
над R- бесконечномерные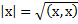
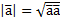
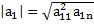
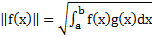
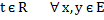
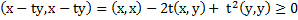

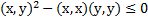
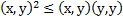
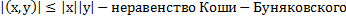
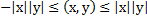
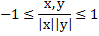
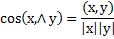
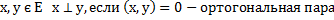
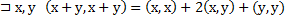
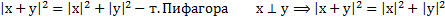
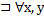
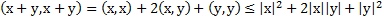
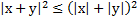
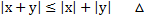
 евклидова пространства называется ортогональным, если все образующие его векторы попарно ортогональны, т.е.
евклидова пространства называется ортогональным, если все образующие его векторы попарно ортогональны, т.е.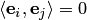 при
при 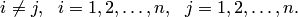
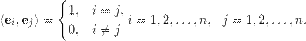
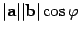 , где
, где  - угол между векторами a и b.
- угол между векторами a и b. , или
, или  , или
, или  . Скалярное произведение вектора на себя, aa, обозначается
. Скалярное произведение вектора на себя, aa, обозначается  .
.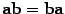 , свойство коммутативности;
, свойство коммутативности;  , свойство дистрибутивности;
, свойство дистрибутивности;  ;
; 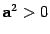 при
при 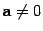 ;
;  ;
;  ;
;  , если
, если  тогда и только тогда, когда векторы a и b ортогональны.
тогда и только тогда, когда векторы a и b ортогональны.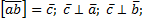
 – образуют правую тройку
– образуют правую тройку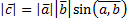

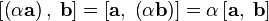
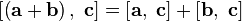
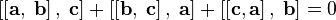
 и нарушается в
и нарушается в 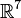



 нормы кватернионов
нормы кватернионов

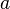 ,
,  и обозначают
и обозначают  либо
либо 
 называют число, которое равно скалярному произведению двух векторов. Первый из них -
называют число, которое равно скалярному произведению двух векторов. Первый из них -  , а второй -
, а второй - 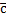 .
.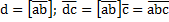
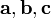 .
.