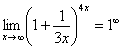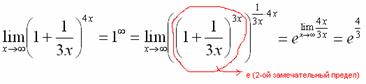|
|
Обзор основных элементарных функций(область определения, возрастание, убывание, нули). 1. Область определения функции — множество, на котором задаётся функция. Если задана функция, которая действует из одного множества в другое, то множество, из которого действует данная функция, называется областью определения. Более формально, пусть задано отображение множество и обозначается 2. Нахождение промежутков возрастания и убывания функции, точек экстремума. Промежутки возрастания и убывания являются решениями неравенств и соответственно. Точки, в которых производная обращается в ноль, называют стационарными. Критическими точками функции называют внутренние точки области определения, в которых производная функции равна нулю или не существует. Мы будем включать критические точки в промежутки возрастания и убывания, если они принадлежат области определения функции. Таким образом, чтобы определить промежутки возрастания и убывания функции o во-первых, находим производную; o во-вторых, находим критические точки; o в-третьих, разбиваем область определения критическими точками на интервалы; o в-четвертых, определяем знак производной на каждом из промежутков. Знак «плюс» будет соответствовать промежутку возрастания, знак «минус» - промежутку убывания.
Пределы функций. Теоремы о пределах функций Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции xn = f(n) целочисленного аргумента n.
Определения пределов функций Определение 1. Постоянное число А называется предел функции f(x) при x→a, если для всякой последовательности {xn} значений аргумента, стремящейся к а, соответствующие им последовательности {f(xn)} имеют один и тот же предел А.Это определение называют определением предел функции по Гейне, или “на языке последовательностей”.
Определение 2. Постоянное число А называется предел функции f(x) при x→a, если, задав произвольное как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех x, лежащих в ε-окрестности числа а, т.е. дляx, удовлетворяющих неравенству Теорема 1. Если существует каждый предел
Теорема 2.
т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности,
Теорема 3.
Первый и второй замечательные пределы. Первый замечательный предел: Рассмотрим следующий предел: В курсе математического анализа, доказывается, что:
Данный математический факт носит название Первого замечательного предела. Нередко в практических заданиях функции могут быть расположены по-другому, это ничего не меняет:
! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде Примеры :
Здесь Но!
Примеры решения:
Второй замечательный предел
В теории математического анализа доказано, что:
Данный факт носит название второго замечательного предела. В качестве параметра может выступать не только переменная x , но и сложная функция. Важно лишь, чтобы она стремилась к бесконечности. Пример:
Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.
Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение
Данная неопределенность как раз и раскрывается с помощью второго замечательного предела.
|
|
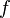 , которое отображает множество
, которое отображает множество 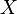 в
в  , то есть:
, то есть: 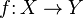 ; тогда
; тогда , или
, или 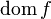 (от англ. domain «область»).
(от англ. domain «область»).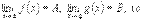


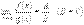 Замечание. Выражения вида 0/0, ∞/∞, ∞-∞, 0*∞, - являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и найти предел такого вида носит название “раскрытие неопределенностей”.
Замечание. Выражения вида 0/0, ∞/∞, ∞-∞, 0*∞, - являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и найти предел такого вида носит название “раскрытие неопределенностей”.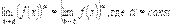
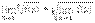 ;
;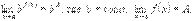
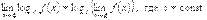
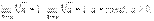
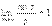
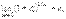 Формулы 1,2 замеч. Предела
Формулы 1,2 замеч. Предела пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида
пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида 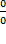
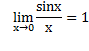
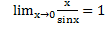 – тот же самый первый замечательный предел.
– тот же самый первый замечательный предел.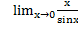 , то и решать его нужно в таком же виде, ничего не переставляя.
, то и решать его нужно в таком же виде, ничего не переставляя.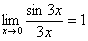
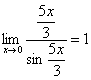
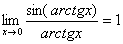
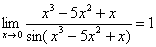
 ,
, 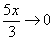 ,
, 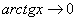 ,
, 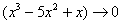
 не правильно, т.к многочлен
не правильно, т.к многочлен 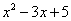 не стремится к нулю, он стремится к пятерке.
не стремится к нулю, он стремится к пятерке.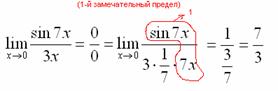
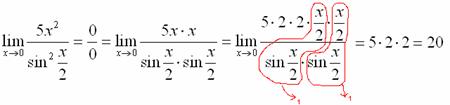
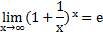
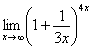
 Нетрудно заметить, что при
Нетрудно заметить, что при 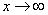 основание степени
основание степени 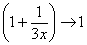 , а показатель –
, а показатель – 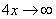 , то есть имеется, неопределенность вида
, то есть имеется, неопределенность вида  :
: