|
|
Матрицы. Матричная алгебра. Определители, их вычисления и свойства.Матрица – таблица элементов. Сложение 2-х одноразмерных матриц - A+B=( Можно умножить матрицу на число. Для этого необходимо умножить все элементы матрица на это число. Для того, чтобы умножать матрицы между собой, число столбцов в первой матрице должно быть равно числу строк во второй (элементы строки первой матрицы умножаются на элементы столбца второй матрицы и складываются меду собой A*B!=B*A Нулевой матрицей, называется матрица соответствующего порядка, состоящая из нулей. Единичной матрицей, называется матрица, в главной диагонали которой стоят единицы Можно использовать операцию транспонирования. Транспонированная матрица — матрица Эквивалентные преобразования. · Строки можно умножить на любое число, отличное от 0. · Можно добавить (убавить) к элементам строки соответствующие элементы другой строки, домноженные на одно и то же число. · Можно вычеркнуть нулевую строчку или столбец. · Две матрицы, названные эквивалентными, если одна получается из другой путем эквивалентных преобразований. Определитель характеризует содержание матрицы. Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. Вычисление определителей. Для матрицы первого порядка, значение детерминанта, равно единственному элементу этой матрицы. Для матрицы второго порядка, значение определителя вычисляется так: Для матриц более высокого порядка, применяем подобные вичисления;
Свойства определителей. (все, что сказано относительно строк, относится и к столбцам). · Определитель основной матрицы равен определителю транспонированной матрицы. · Общий множитель в строке можно выносить за знак определителя. · Если матрицу · Если каждый элемент в какой-то из строк определителя равен сумме 2-х слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем. · Если 2 строки определителя поменять местами, то определитель поменяет знак. · Определитель с 2-я равными строками, равен 0. · Определитель с двумя пропорциональными строками, равен 0. · Определитель, содержащий нулевую строку, равен 0. · Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число. · Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов · Определитель произведения матриц равен произведению определителей:
Решение систем алгебраических уравнений методом Крамера. Матричный метод решения систем уравнений. В линейных алгебраических уравнениях из коэффициентов, стоящих перед неизвестным радикалом можно составить матрицу, если добавить к ней еще один столбец (составленный из значений, расположенных справа от знака равенства), то получим расширенную матрицу. Система уравнений считается совместной, если имеет минимум одно решение, только тогда, когда ранг матрицы, равен рангу расширенной матрицы. Совместная система имеет одно решение – определенная. Совместная система имеет несколько решений – неопределенная. Если решений нет система– не совместная. Метод Крамера.
Матричный метод.
Миноры матрицы. Ранг матрицы. Элементарные преобразования матриц. Теорема о сохранении ранга матрицы при элементарных преобразованиях. Миноры матрицы. Минорами первого порядка являются сами элементы матрицы. Миноры второго порядка – определители, которые получаются следующим образом: выбирают любые две строки с любых двух столбцов и вычеркивают их.Из них ищут определитель второго порядка. Пример. Как оптимизировать работу по поиску миноров, отличных от нуля? 1. По определителю 2. По окаймляющим минорам 3. Метод Гаусса-Жордана (Предпочтительный) Пример. Ранг матрицы. Рангом матрицыAназывают число, которое является наивысшим порядком минора матрицы, отличного от нуля. Для чего ранг: Если мы решаем СЛАУ и записываем основную матрицу для этой матрицы, окажется вычисленным ранг основной матрицы и делаем вывод: сколько строк входит в этот минор наивысшего порядка (а определитель называется базисным минором), столько и уравнений, их нужно оставить. То есть уравнения, коэффициенты которых не вошли в базисный минор, эти уравнения надо отбросить. |
|
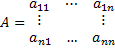
 ).
).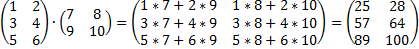 , матрицу
, матрицу  и
и  перемножить нельзя).
перемножить нельзя). .
. , полученная из исходной матрицы A, заменой строк на столбцы.
, полученная из исходной матрицы A, заменой строк на столбцы.  и
и  .
.  .
.
 n-го порядка, умножить на ненулевое число, то определитель будет равен произведению определителя исходной матрицы на это число в степени порядка матрицы.
n-го порядка, умножить на ненулевое число, то определитель будет равен произведению определителя исходной матрицы на это число в степени порядка матрицы. .
. .
. , где
, где  - исходный определитель матрицы,
- исходный определитель матрицы,  - i-ый столбец заменяем на свободные члены справа.
- i-ый столбец заменяем на свободные члены справа. ,
,  ,
, ,
,  ,
,  ,
, ,
, ,
, .
.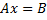 ,
,  , Ex=
, Ex=  ,
,  ,
, 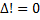
 ,
,  ,
, 
 ,
,  ,
, 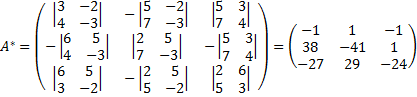
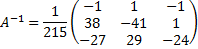
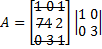
 Сколько единиц – такой и ранг.
Сколько единиц – такой и ранг.