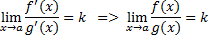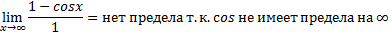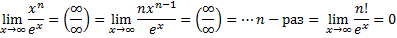|
|
Производная высших порядков. Дифференциал высших порядков.Дифференциал высших порядков. Пусть y=f(u) , где u=у(x) (у зависит от х) Существует производные Мы знаем, что Диф-ал
Свойства инвариантности(неизменности) первого диф-ала заключается в тои, что форма слева и справа одинакова (сохранение вида диф-ала) Инвариантность относительно аргуманта
Мы находимся слева (форма записи диф-циала), где х-независима Если мы находимся слева, то первая производная равна Справа, отмечаем, что второй диф-циал и диф-циал высших порядков свойством инвариантности не обладают. 26. Основные теоремы дифференциального вычисления (Ролля, Логранжа, Коши). Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения) Пусть функция 1. непрерывна на отрезке 2. дифференцируема на интервале 3. на концах отрезка Тогда на интервале Следствие. (Геометрический смысл теоремы Ролля) Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс. Следствие. Если Теорема Лагранжа Теорема Лагранжа. (О конечных приращениях) Пусть функция 1. непрерывна на отрезке 2. дифференцируема на интервале Тогда на интервале
Замечание Теорема Ролля есть частный случай теоремы Лагранжа, когда Следствие. (Геометрический смысл теоремы Лагранжа) На кривой
Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:
Теорема Коши Теорема Теорема Коши. (Об отношении конечных приращений двух функций) Если функции 1. непрерывны на отрезке 2. дифференцируемы на интервале 3. производная тогда на этом интервале найдется по крайней мере одна точка
Правила Лопиталя (2). 1. Неопределенность ( Доказательство: Рассмотрим При условиях, которые дает Лопиталь, утверждается возможность находить предел отношения функций следующим образом: -найти производную в числителе и знаменателе, поделить.
Замечания: · Может оказаться, что I требование заменяется Все остальные требования выполняются · Может быть, что после применения правила Лопиталя, мы снова получим неопределенность ( · Если после применения получим какую-то дробь
Тогда мы говорим, что пределом является бесконечность. 2. Неопределенность Если две функции f(x) и g(x) стремяться к | x->a И существует предел отношения производных, равный k, то этому же числу равняется
Замечания: · Пример показывает, что если правило Лопиталя не дает ответа, то предел отношения может существовать все равно, но нужно искать другим вариантом.
· Правило Лопиталя можно применять много раз |
|
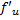 и
и 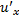
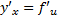 *
* 
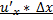 где х-независимая переменная =
где х-независимая переменная = 
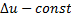
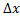 dx=
dx= 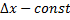
 Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную
функции f:
Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную
функции f:
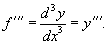 Производные более высокого порядка (если они существуют), определяются как
Производные более высокого порядка (если они существуют), определяются как
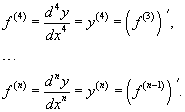 или
или

 и здась числитель можно оторвать от знаменателся
и здась числитель можно оторвать от знаменателся 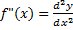 ;
;  .
.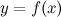
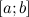 ;
;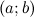 ;
; .
. , в которой
, в которой  .
.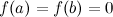 , то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.
, то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.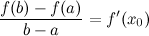
 и
и 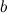 найдется точка
найдется точка  , такая, что через эту точку можно провести касательную, параллельную хорде
, такая, что через эту точку можно провести касательную, параллельную хорде  (рис. 1).
(рис. 1).
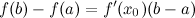
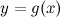 :
: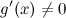 на интервале
на интервале 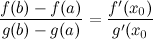
 )
)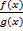 не оперделена в точке «а», и справедливо условие теоремы Коши. Существует предел отношения:
не оперделена в точке «а», и справедливо условие теоремы Коши. Существует предел отношения: 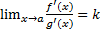 тогда: Предел отношения функций тоже равняется k
тогда: Предел отношения функций тоже равняется k 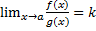 . Заметим, что правило Лопиталя дает достаточное условие существования предела функции.
. Заметим, что правило Лопиталя дает достаточное условие существования предела функции.
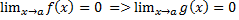
 где числитель число, а знаменатель-0, то
где числитель число, а знаменатель-0, то 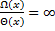

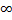 при х->a и обе функции дифференцируемы в окрестностях точки «а»
при х->a и обе функции дифференцируемы в окрестностях точки «а»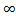 |
|