|
|
Цилиндры с образующей, параллельной одной из координатных осейЦилиндрической поверхностью называется поверхность, образованная движением прямой, что пересекает заданную линию и параллельную заданному направлению. Заданная линия, через точки которой проходит прямая, которая перемещается, называется направляющей, а каждое положение такой прямой называется образующей рассматриваемой цилиндрической поверхности. Выберем координатную систему так, чтобы одна из осей, например z, была параллельной заданному направлению и будем рассматривать тот, хоть и частный, но очень важный случай, когда направляющая линия лежит в плоскости, перпендикулярной заданному направлению. Тогда без всякого ограничения общности исследования возможно считать, что направляющая лежит в плоскости ху. Пусть в плоскости z=0 уравнение направляющей имеет вид F(х,у)=0 , и , таким образом, такая линия задана двумя уравнениями Z=0, F(x;y)=0 (1) Докажем, что рассматриваемой цилиндрической поверхности отвечает уравнение F(x;y)=0 (2), то есть, что координаты любой точки поверхности отвечают уравнению (2), а координаты любой точки, что не лежит на этой поверхности, ему не отвечают. Пусть М0(х0;у0;0) - любая точка направляющей (рис. 26).
Проведем через М0 прямую L, параллельную оси z, и выберем на ней произвольную точку М1. Координаты этой точки (х0;у0;z1).. Согласно предположению координаты точки М0 отвечают системе Z=0, F(x;y)=0. Следовательно, F(x0;y0)=0 и координаты точки М1 (при любом z1) отвечают уравнению F(x;y)=0. Таким образом, координаты любой точки М1 прямой L отвечают уравнению F(x;y)=0. Но М0 - произвольная точка направляющей. Следовательно, координаты любой точки любой образующей; то есть координаты любой точки рассматриваемой цилиндрической поверхности отвечают уравнению F(x;y)=0. Пусть теперь выбрана любая точка Очевидно, что если образующие цилиндрической поверхности параллельны оси у, а уравнение направляющей имеет вид у=0, F(x;z)=0, то уравнение цилиндрической поверхности F(x; z)=0. Аналогично для цилиндрической поверхности, образующие которой параллельны оси х, имеем уравнение F(y; z)=0 Поверхности вращения Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой). Например, если прямая пересекает ось вращения, то при её вращении получится коническая поверхность, если параллельна оси — цилиндрическая, если скрещивается с осью — однополостный гиперболоид вращения. Одна и та же поверхность может быть получена вращением самых разнообразных кривых. Площадь поверхности вращения, образованной вращением плоской кривой конечной длины вокруг оси, лежащей в плоскости кривой, но не пересекающей кривую, равна произведению длины кривой на длину окружности с радиусом, равным расстоянию от оси до центра масс кривой. Это утверждение называется второй теоремой Паппа — Гульдина, или теоремой Паппа о центроиде. Например, для тора с радиусами
Эллипсоиды Эллипсо́ид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. Каноническое уравнение эллипсоида в декартовых координатах, совпадающих с осями деформации эллипсоида:
Величины a, b, c называют полуосями эллипсоида. Также эллипсоидом называют тело, ограниченное поверхностью эллипсоида. Эллипсоид представляет собой одну из возможных форм поверхностей второго порядка. В случае, когда пара полуосей имеет одинаковую длину, эллипсоид может быть получен вращением эллипса вокруг одной из его осей. Такой эллипсоид называют эллипсоидом вращения или сфероидом. Эллипсоид более точно, чем сфера, отражает идеализированную поверхность Земли. Объём эллипсоида:
Площадь поверхности эллипсоида вращения
Гиперболоиды Гиперболоид (от др.-греч. ὑπερβολή — гипербола, и εἶδος — вид, внешность). В математике гиперболоид — это видповерхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением
или
где a и b — мнимые полуоси, а c — действительная полуось. Если a = b, то такая поверхность называется гиперболоидом вращения. Однополостный гиперболоид вращения может бытьполучен вращением гиперболы вокруг её мнимой оси, двухполостный — вокруг действительной. Двуполостный гиперболоид вращения также является геометрическим местом точек P, модуль разности расстояний от которых до двух заданных точек A и B постоянен: Однополостный гиперболоид является дважды линейчатой поверхностью; если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней. Параболоиды Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка. Канонические уравнения параболоида в декартовых координатах:
· если · если · если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром. Конусы Ко́нус (от др.-греч. κώνος «шишка») — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание). Если основание конуса представляет собой многоугольник, такой конус является пирамидой. Свойства Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.
Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания. Телесный угол при вершине прямого кругового конуса равен
где α — угол раствора конуса. Площадь боковой поверхности такого конуса равна
а полная площадь поверхности (т. е. сумма площадей боковой поверхности и основания)
Объём кругового конуса равен
Для усечённого конуса (не обязательно прямого и кругового) объём равен:
Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).
15.* Собственные векторы матрицы минимального оператора. Собственный вектор — понятие в линейной алгебре, определяемое для квадратной матрицы или произвольного линейного преобразования как вектор, умножение матрицы на который или применение к которому преобразования даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение, называемое собственным числом матрицы или линейного преобразования. Пусть Собственным вектором линейного преобразования
Собственным значением линейного преобразования Упрощённо говоря, собственный вектор — любой ненулевой вектор |
|
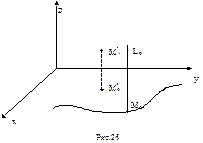
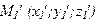 , что не лежит на рассматриваемой цилиндрической поверхности. Рассмотрим точку
, что не лежит на рассматриваемой цилиндрической поверхности. Рассмотрим точку 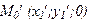 , что является проекцией точки М1¢ на плоскость ху. Точка М0¢ не лежит на заданной направляющей линии (иначе говоря, точка М1¢ лежала бы на заданной поверхности). А потому координаты точки М0¢ не могут удовлетворять системе уравнений Z=0, F(x;y)=0. Но первое уравнение, наверное, выполнено. Следовательно
, что является проекцией точки М1¢ на плоскость ху. Точка М0¢ не лежит на заданной направляющей линии (иначе говоря, точка М1¢ лежала бы на заданной поверхности). А потому координаты точки М0¢ не могут удовлетворять системе уравнений Z=0, F(x;y)=0. Но первое уравнение, наверное, выполнено. Следовательно 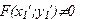 . Но это означает, что координаты точки
. Но это означает, что координаты точки 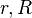 , площадь поверхности равна
, площадь поверхности равна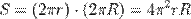 .
. где
где  — произвольные положительные числа.
— произвольные положительные числа.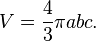
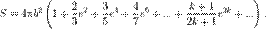
 (однополостный гиперболоид), где a и b — действительные полуоси, а c — мнимая полуось;
(однополостный гиперболоид), где a и b — действительные полуоси, а c — мнимая полуось; (двуполостный гиперболоид),
(двуполостный гиперболоид), . В этом случае A и B называются фокусами гиперболоида.
. В этом случае A и B называются фокусами гиперболоида.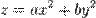
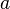 и
и  одного знака, то параболоид называется эллиптическим.
одного знака, то параболоид называется эллиптическим.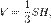 где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.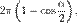
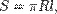
 где R — радиус основания, l — длина образующей.
где R — радиус основания, l — длина образующей.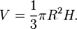
 где S1 и S2 — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, h и H — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.
где S1 и S2 — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, h и H — расстояния от плоскости соответственно верхнего и нижнего основания до вершины. — линейное пространство над полем
— линейное пространство над полем 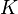 ,
, 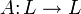 — линейное преобразование.
— линейное преобразование. называется такой ненулевой вектор
называется такой ненулевой вектор  , что для некоторого
, что для некоторого 
 .
.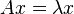 имеет ненулевое решение
имеет ненулевое решение  , который отображается оператором в коллинеарный
, который отображается оператором в коллинеарный 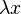 , а соответствующий скаляр
, а соответствующий скаляр  называется собственным значением оператора.
называется собственным значением оператора.