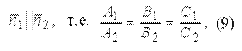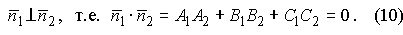|
|
Взаимное расположение плоскостей.Две плоскости в пространстве могут совпадать. В этом случае они имеют, по крайней мере, три общие точки. Две плоскости в пространстве могут пересекаться. Пересечением двух плоскостей является прямая линия, что устанавливается аксиомой: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Отдельный интерес представляет случай, когда угол между плоскостями равен девяноста градусам. Такие плоскости называют перпендикулярными. Наконец, две плоскости в пространстве могут быть параллельными, то есть, не иметь общих точек. Рекомендуем ознакомиться со статьей параллельность плоскостей, чтобы получить полное представление об этом варианте взаимного расположения плоскостей. Способы задания плоскости. Во-первых, плоскость можно задать, зафиксировав три не лежащие на одной прямой точки пространства. Этот способ основан на аксиоме: через любые три точки, не лежащие на одной прямой, проходит единственная плоскость. Два следующих способа задания плоскости являются следствием из предыдущего. Они основаны на следствиях из аксиомы о плоскости, проходящей через три точки: · через прямую и не лежащую на ней точку проходит плоскость, притом только одна; · через две пересекающиеся прямые проходит единственная плоскость. Четвертый способ задания плоскости в пространстве основан на определении параллельных прямых. Таким образом, указав две параллельные прямые в пространстве, мы определим единственную плоскость, в которой эти прямые лежат. Признак параллельности двух плоскостей дает нам еще один способ задания плоскости. Вспомним формулировку этого признака: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то такие плоскости параллельны. Следовательно, мы можем задать конкретную плоскость, если укажем точку, через которую она проходит и плоскость, которой она параллельна.
Нормальные уравнения плоскости. · Чтобы вывести уравнение геометрического места точек, надо: взять на этом геометрическом месте текущую точку M, принадлежащую геометрическому месту точек и считать ее известной, а затем связать координаты этой точки с помощью условий задачи. · Чтобы привести общее уравнение к нормальному виду, надо: умножить обе части уравнения на координатный множитель M, вычислить этот множитель по формуле: Расстояние от точки до плоскости. Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость. · Отклонение точки
· Расстояние
Угол между двумя плоскостями. Угол между двумя плоскостями, точнее, один из двух смежных углов между двумя плоскостями, может быть вычислен как угол между нормальными векторами этих плоскостей. Если плоскости заданы своими общими уравнениями
то их нормальные векторы имеют вид
Условие параллельности. Условием параллельности двух плоскостей является условие
Условие перпендикулярности. Условием перпендикулярности двух плоскостей является условие:
ВЫВОД: Мы рассмотрели разные виды уравнений плоскости в пространстве. Заметим, что при выборе уравнений плоскости используют либо скалярное произведение, если хотят зафиксировать ортогональность. Если хотят отметить колиниарность, то вычисляют векторное произведение, и оно равно нулю. Или говорят о пропорциональности соответственных координат. Если фиксируют компланарность трёх векторов, тогда смешанное произведение равно нулю. |
|
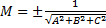 , а затем выбрать знак, противоположный знаку D (свободный член в общем уравнении).
, а затем выбрать знак, противоположный знаку D (свободный член в общем уравнении). от плоскости заданной нормированным уравнением
от плоскости заданной нормированным уравнением 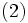
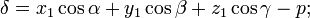
 ,если
,если  и начало координат лежат по разные стороны плоскости, в противоположном случае
и начало координат лежат по разные стороны плоскости, в противоположном случае  . Расстояние от точки до плоскости равно
. Расстояние от точки до плоскости равно 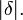
 от точки
от точки  , до плоскости, заданной уравнением
, до плоскости, заданной уравнением 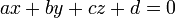 , вычисляется по формуле:
, вычисляется по формуле: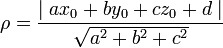

 и потому угол Θ между плоскостями находим по формуле
и потому угол Θ между плоскостями находим по формуле