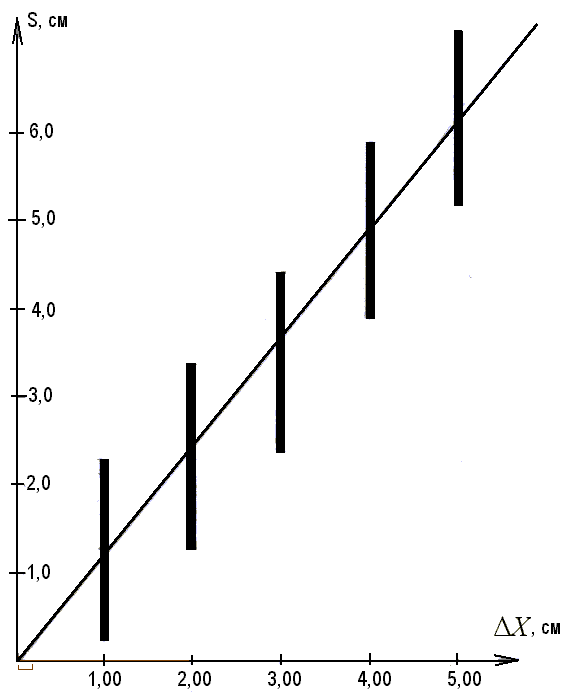|
|
Брошенного горизонтально, от начальной скорости, сообщенной телу1. Система действий по получению и обработке результатов измерения начальной скорости (сжатия пружины) и дальности полета тела: 1) проверить, нужно ли ввести поправку; если да, то ввести поправку; 2) установить, сколько измерений данной величины нужно произвести; 3) подготовить таблицу для записи и обработки результатов наблюдений; 4) произвести установленное число измерений данной величины; результаты наблюдений занести в таблицу; 5) найти измеренное значение величины как среднее арифметическое результатов отдельных наблюдений с учетом правила запасной цифры:
6) вычислить модули абсолютных отклонений результатов отдельных измерений от среднего: 7) найти случайную погрешность; 8) найти инструментальную погрешность; 9) найти погрешность отсчета; 10) найти погрешность вычисления; 11) найти полную абсолютную погрешность; 12) записать результат с указанием полной абсолютной погрешности.
2. Система действий по построению графика зависимости S = f(Δх): 1) начертить координатные оси; ось абсцисс обозначить Δх, см, а ось ординат – S, м; 2) выбрать масштабы для каждой из осей и нанести на осях шкалы; 3) изобразить интервалы значений S и Δх для каждого опыта; 4) провести плавную линию так, чтобы она проходила внутри интервалов.
3. ОИ № 1 – стальной шарик диаметром 2 см: 1) сжатие пружины Δх измеряли металлической линейкой с миллиметровыми делениями. Дальность полета измеряли стандартной школьной линейкой с сантиметровыми делениями. Поправки не вводим – не нужно; 2) при измерениях S в одинаковых условиях и при одном и том же сжатии пружины обнаружили разброс значений. Отсюда сделали вывод о существовании случайной погрешности. Решили, что должно быть проведено 5 измерений S при одном и том же Δх. При измерении Δх разброс значений не обнаружен. Поэтому будем считать, что абсолютная погрешность при измерении Δх равна инструментальной погрешности, которая для выбранной металлической линейки с миллиметровыми делениями равна половине цены деления 0,05 см (см. табл. 3); 3) таблица для записи результатов измерений и их обработки: ОИ № 1 – стальной шарик.
4) результаты проведенных измерений занесены в таблицу; 5) среднее арифметическое каждого измерения S вычислено и указано в предпоследней строке таблицы; 6) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для первого опыта:
7) находим случайную погрешность измерения:
8) находим инструментальную погрешность линейки (см. табл. 3): ΔSи = δ = 1,0 cм; 9) погрешность отсчета по данной линейке принимаем равной половине цены деления: ΔSо= 0,5 см; 10) погрешность вычисления в данном случае равна нулю; 11) рассчитываем полную абсолютную погрешность: ΔS = ΔSC + ΔSи + ΔS0 + ΔSB = 0,96 +1,0 + 0,5 + 0,0 = 2,46 см ≈ 2,5 см (здесь окончательный результат округлен с избытком до одной значащей цифры); 12) записываем результат измерения: S = (12,4 ± 2,5) см. 6 а) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для второго опыта:
7 а) находим случайную погрешность измерения:
8 а) инструментальная погрешность линейки ΔSи = δ = 1,0 cм; 9 а) погрешность отсчета по данной линейке равна половине цены деления ΔSо = 0,5 см; 10 а) погрешность вычисления в данном случае равна нулю; 11 а) рассчитываем полную абсолютную погрешность: ΔS = ΔSC + ΔSи + ΔS0 + ΔSB = 1,2 + 1,0 + 0,5 + 0,0 = 2,7 см; 12 а) записываем результат измерения: S = (24,5 ± 2,7) см.
6 б) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для третьего опыта:
7 б) находим случайную погрешность измерения:
8 б) инструментальная погрешность линейки ΔSи = δ = 1,0 cм; 9 б) погрешность отсчета по данной линейке ΔSо = 0,5 см; 10 б) погрешность вычисления в данном случае равна нулю; 11 б) рассчитываем полную абсолютную погрешность: ΔS = ΔSC + ΔSи + ΔS0 + ΔSB = 1,08 + 1,0 + 0,5 + 0,0 = 2,58 см ≈ 2,6 см; 12 б) записываем результат измерения: S = (36,7 ± 2,6) см.
6 в) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для четвертого опыта:
7 в) находим случайную погрешность измерения:
8 в) инструментальная погрешность линейки ΔSи = δ = 1,0 cм; 9 в) погрешность отсчета по данной линейке ΔSо = 0,5 см; 10 в) погрешность вычисления в данном случае равна нулю; 11 в) рассчитываем полную абсолютную погрешность: ΔS = ΔSC + ΔSи + ΔS0 + ΔSB = 0,72 + 1,0 + 0,5 + 0,0 = 2,22 см ≈ 2,2 см; 12 в) записываем результат измерения: S = (48,8 ± 2,2) см.
6 г) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для пятого опыта:
7 г) находим случайную погрешность измерения:
8 г) инструментальная погрешность линейки ΔSи = δ = 1,0 cм; 9 г) погрешность отсчета по данной линейке ΔSо = 0,5 см; 10 г) погрешность вычисления в данном случае равна нулю; 11 г) рассчитываем полную абсолютную погрешность: ΔS = ΔSC + ΔSи + ΔS0 + ΔSB = 0,72 + 1,0 + 0,5 + 0,0 = 2,22 см ≈ 2,2 см; 12 г) записываем результат измерения: S = (61,2 ± 2,2) см. Результаты обработки всех измерений приведены в последней строке таблицы.
4. Построим график зависимости дальности полета стального шарика от смещения пружины от положения равновесия, последовательно выполняя соответствующие действия. При построении во всех случаях указанный интервал погрешности ΔS в масштабе соответствует длине линии на графике. Толщина линии соответствует погрешности измерения Δх. 5. Построенный график похож на график прямой пропорциональной зависимости y = kx. Значение коэффициента k для данного тела нетрудно определить из графика: k = 0,12x (м). Для стального шарика диаметром 2 см дальность его полета прямо пропорциональна смещению пружины, которая сообщает ему начальную скорость.
Рис. 12. График зависимости дальности полета стального шарика от деформации пружины
6. ОИ № 2 – пластмассовый шарик диаметром 4 см. 3) Таблица для записи результатов измерений и их обработки: ОИ № 2 – пластмассовыйшарик.
4) результаты проведенных измерений занесены в таблицу; 5) среднее арифметическое каждого измерения S вычислено и указано в предпоследней строке таблицы; 6) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для первого опыта:
7) находим случайную погрешность измерения:
8) инструментальная погрешность линейки ΔSи = δ = 1,0 cм; 9) погрешность отсчета по данной линейке ΔSо = 0,5 см. 10) погрешность вычисления в данном случае равна нулю; 11) рассчитываем полную абсолютную погрешность: ΔS = ΔSC + ΔSи + ΔS0 + ΔSB = 0,9 + 1,0 + 0,5 + 0,0 = 2,4 см; 12) записываем результат измерения: S = (1,3 ± 2,4) см
6 а) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для второго опыта:
7 а) находим случайную погрешность измерения:
8 а) инструментальная погрешность линейки ΔSи = δ = 1,0 cм; 9 а) погрешность отсчета по данной линейке ΔSо = 0,5 см; 10 а) погрешность вычисления в данном случае равна нулю; 11 а) рассчитываем полную абсолютную погрешность: ΔS = ΔSC + ΔSи + ΔS0 + ΔSB = 0,36 + 1,0 + 0,5 + 0,0 = 1,86 см; 12 а) записываем результат измерения: S = (2,3 ± 1,86) см 6 б) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для третьего опыта:
7 б) находим случайную погрешность измерения:
8 б) инструментальная погрешность линейки ΔSи = δ = 1,0 cм; 9 б) погрешность отсчета по данной линейке ΔSо = 0,5 см; 10 б) погрешность вычисления в данном случае равна нулю; 11 б) рассчитываем полную абсолютную погрешность: ΔS = ΔSC + ΔSи + ΔS0 + ΔSB = 0,48 + 1,0 + 0,5 + 0,0 = 1,98 см ≈ 2,0 см; 12 б) записываем результат измерения: S = (3,4 ± 2,0) см
6 в) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для четвертого опыта:
7 в) находим случайную погрешность измерения:
8 в) инструментальная погрешность линейки ΔSи = δ = 1,0 cм; 9 в) погрешность отсчета по данной линейке ΔSо= 0,5 см; 10 в) погрешность вычисления равна нулю; 11 в) рассчитываем полную абсолютную погрешность: ΔS = ΔSC + ΔSи + ΔS0 + ΔSB = 0,48 +1,0 + 0,5 + 0,0 = 1,98 см ≈ 2,0 см. 12 в) записываем результат измерения: S = (4,9 ± 2,0) см
6 г) рассчитываем модули абсолютных отклонений результатов отдельных наблюдений от среднего для пятого опыта:
7 г) находим случайную погрешность измерения:
8 г) инструментальная погрешность линейки ΔSи = δ = 1,0 cм; 9 г) погрешность отсчета по данной линейке ΔSо = 0,5 см; 10 г) погрешность вычисления равна нулю; 11 г) рассчитываем полную абсолютную погрешность: ΔS = ΔSC + ΔSи + ΔS0 + ΔSB = 0,72 + 1,0 + 0,5 + 0,0 = 2,22 см ≈ 2,2 см; 12 г) записываем результат измерения: S = (6,2 ± 2,2) см. Результаты обработки всех измерений приведены в последней строке таблицы. 4. Построим график зависимости дальности полета пластмассового шарика от деформации пружины (рис. 13).
Рис. 13. График зависимости дальности полета пластмассового шарика от деформации пружины
5. Устанавливаем, что полученный нами график похож на график прямой пропорциональной зависимости y = kx. Значение коэффициента k для данного тела нетрудно найти из графика. Поэтому окончательно можно записать y = 0,012x (м). Ответ на ПЗ: для пластмассового шарика дальность полета прямо пропорциональна деформации пружины, сообщающей ему начальную скорость. 6. Общий вывод: для тела, брошенного горизонтально, дальность полета прямо пропорциональна скорости, приобретенной телом в начальный момент времени. Пример 2.Исходная ситуация. При решении познавательной задачи «Зависит ли изменение температуры тела от количества теплоты, полученной телом при нагревании?» в качестве объектов исследования были выбраны вода и подсолнечное масло, то есть задача решалась только для жидкостей. В опыте с водой было взято 100 г воды, изначально находящейся при комнатной температуре (18 0С). Количество теплоты считалось пропорциональным времени горения одной и той же спиртовки. Опыт проводился по следующей методике. Жидкость нагревалась до фиксированной температуры, измерялось время нагрева. Результаты измерений заносили в таблицу, горелку убирали и охлаждали жидкость до комнатной температуры. После этого вновь подносили горелку и грели жидкость до новой фиксированной температуры. Нагрев велся до достижения предела измерения термометра (100 0С). Было установлено, что изменение температуры воды зависит от сообщенного количества теплоты: чем больше количество теплоты, тем больше изменение температуры воды. Методика проведения опыта с подсолнечным маслом была такой же. Ответ на познавательную задачу был аналогичным предыдущему: изменение температуры подсолнечного масла зависит от сообщенного количества теплоты: чем больше количество теплоты, тем больше изменение температуры подсолнечного масла. Затем был сделан общий вывод: изменение температуры жидкости зависит от сообщенного ей количества теплоты: чем больше количество теплоты, тем больше изменение температуры жидкости. Теперь нужно решить следующуюПЗ: установить вид зависимости изменения температуры жидкости при нагревании от времени нагрева. Для решения этой задачи нужно выполнить следующие действия. 1. Составить систему действий по получению и обработке результатов измерения времени нагрева жидкостей от начальной (комнатной) температуры до указанной и изменения температуры жидкостей (см. п. 2.2.8 или п. 2.2.9). 2. Составить систему действий по построению графика зависимости изменения температуры жидкости от времени нагрева. 3. Выбрать ОИ № 1 – воду массой 100 г и начальной температурой 18 0С и выполнить все запланированные в п. 1 и 2 действия. 4. Подобрать известную в математике функциональную зависимость, график которой похож на экспериментальную кривую. 5. Записать математически эту функциональную зависимость для воды и сформулировать для нее ответ на поставленную познавательную задачу. 6. Выбрать ОИ № 2 – подсолнечное масло и выполнить с ним ту же систему действий. 7. Подобрать известную в математике функциональную зависимость, график которой похож на экспериментальную кривую. 8. Записать математически эту функциональную зависимость для подсолнечного масла и сформулировать для него ответ на поставленную познавательную задачу. 9. Сформулировать функциональную зависимость между величинами в обобщенном виде. |
|
































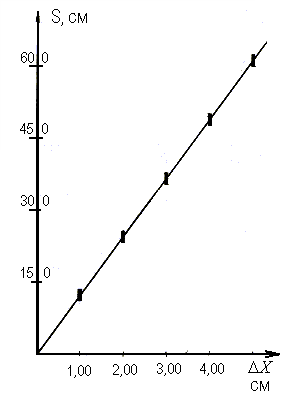
 .
.




 .
.









 ;
;





 .
.