|
|
Действие данной системы сил на абсолютно твердое тело не изменяется, если к ней прибавить или от нее отнять уравновешенную систему сил.Введение к курсу лекций
Содержание дисциплины «Механика» по образовательному стандарту, утверждённому в 2010г. С.3 Профессиональный цикл Базовая (общепрофессиональная) часть Механика Знать: основные понятия прикладной механики: растяжение-сжатие, сдвиг, прямой поперечный изгиб, кручение, косой изгиб, элементы рационального проектирования простейших систем, основы механики упругой среды, продольные и поперечные волны, основные понятия теории механизмов и машин, основные виды механизмов, основы конструирования и стадии разработки измерительных приборов; Уметь: - выполнять анализ напряжённого и деформированного состояния в точке тела вследствие продольно-поперечного изгиба, удара, усталости;
На кафедре ТЭА имеется научная школа, выполняются теоретические и экспериментальные исследования, направленные на повышение надёжности и долговечности машин и другого оборудования. Разрабатываются методы испытания материалов, приборы. В этой работе традиционно участвуют и студенты. Тем, кто будет изучать представленный материал, рекомендуется принять участие в научно-исследовательской работе кафедры, выступить с докладами на студенческих и других научных конференциях. Такие научные исследования могут иметь продолжение в дальнейшей учёбе и профессиональной деятельности.
Наука о механическом движении и взаимодействии материальных тел называется механикой. Она изучает механические процессы в природе и технике. С развитием этой науки в ней появился целый ряд самостоятельных областей: теория упругости, теория пластичности, гидромеханика, аэромеханика, газовая динамика и ряд разделов так называемой прикладной механики (сопротивление материалов, статика сооружений, теория механизмов и машин, гидравлика, детали машин). В каждом разделе механики используются свои специфические закономерности и методы, но все они построены на основных законах или принципах, понятиях, методах, общих для всех областей механики. Рассмотрение этих общих понятий, законов и методов и составляет предмет теоретической (или общей) механики. Роль и значение теоретической механики в инженерном образовании определяется тем, что она является научной базой очень многих областей современной техники и строительства. Одновременно законы и методы механики, как естественной науки, т.е. науки о природе, позволяют изучить и объяснить целый ряд важных явлений в окружающем нас мире и способствуют дальнейшему росту и развитию естествознания в целом. (Движение планет, падение камня ит.д.). Изучение этого предмета даёт будущему специалисту способность представить адекватную современному уровню знаний научную картину мира, выявить естественнонаучную сущность проблем, возникающих в ходе профессиональной деятельности. Изучение механики развивает способность использовать физико-математический аппарат, собирать, обрабатывать, анализировать научно-техническую информацию, участвовать в монтаже и наладке оборудования.
Раздел I. Теоретическая механика
Механическим движением называют происходящее с течением времени изменение взаимного положения материальных тел в пространстве. Под механическим взаимодействием понимают те действия материальных тел друг на друга, в результате которых происходит изменение движения этих тел или изменение их формы и размеров (деформация). За основную меру этих действий принимают величину, называемую силой. В основе механики лежат законы, называемые законами классической механики (или законами Ньютона), которые установлены путём обобщения результатов многочисленных опытов и наблюдений и подтверждены практикой. Современное развитие науки показывает, что при скоростях, близких к скорости света, движение тел подчиняется законам механики теории относительности, а движение микрочастиц (электроны, позитроны и др.) описывается законами квантовой механики. Однако эти открытия только уточнили область приложений классической механики и подтвердили достоверность её законов для движений всех тел, отличных от микрочастиц, при скоростях, не близких к скорости света, т. е. для тех движений, которые имеют огромное практическое значение в технике, небесной механике и ряде других областей естествознания. По характеру рассматриваемых задач теоретическую механику принято разделять на статику, кинематику, и динамику. В таком же порядке излагается материал в данном курсе (см. также [1, 4]), что облегчает подготовку к решению задач. В литературе можно встретить и другие варианты последовательности изложения теоретического материала [10].
Статика Введение Статикой называется раздел механики, в котором излагается общее учение о силах и изучаются условия равновесия материальных тел, находящихся под действием сил. Для понимания раздела статики необходимо знать следующие сведения. Из математики – теорему синусов, теорему косинусов, площадь треугольника, сложение векторов, векторное произведение двух векторов. Из физики – законы Ньютона. Рекомендуется повторить эти темы.
Основные понятия и аксиомы статики
Общий метод научных исследований состоит в том, что при рассмотрении того или иного явления в нём выделяют главное, определяющее, а от всего остального, сопутствующего данному явлению, абстрагируются. В результате вместо реального явления или объекта рассматривают некоторую его модель и вводят ряд абстрактных понятий, отражающих соответствующие свойства этого явления (объекта). К числу таких понятий в «Статике» относятся: материальная точка, абсолютно твёрдое тело, сосредоточенная сила. Материальной точкой называют материальное тело, размеры которого в рассматриваемых конкретных условиях можно не учитывать. Материальная точка обладает массой и способностью взаимодействовать с другими телами. Например, при изучении движения планет Солнечной системы вокруг Солнца их размерами по сравнению с их расстояниями от Солнца пренебрегают и рассматривают эти планеты как материальные точки. Системой материальных точек (или механической системой) называется такая совокупность материальных точек, в которой положение и движение каждой точки зависит от положения и движения других точек этой системы. Абсолютно твёрдым телом называют такое тело, расстояние между каждыми двумя точками которого всегда остаётся постоянным. Сила. Математическое определение силы даёт второй закон Ньютона (см. курс физики и раздел динамики данного курса). Словесные формулировки разных авторов несколько отличаются друг от друга. По Ньютону, приложенная сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного прямолинейного движения. Т.о. сила оценивается по её действию, которое проявляется в изменении движения тела. В данном случае под телом понимается материальная точка, т.е. предполагается отсутствие вращательного движения тела. Кирхгоф предложил рассматривать силу по определению как производную от импульса. Силой называют меру механического воздействия в данное мгновение на материальную частицу со стороны других материальных тел, учитывающую величину и направление этого воздействия [10]. Сила – это мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия [4]. Сила – векторная величина. Сила полностью задана, если указаны её: 1) численное значение, т.е. модуль, 2) направление и 3) точка приложения. Единица измерения силы – Ньютон (Н). Взаимодействие между телами, как это следует из первого закона Ньютона, является причиной изменения состояния их движения. Кроме того, оно вызывает также деформацию тел. Измеряя деформации Dl1, Dl2 одного и того же упругого тела под действием двух одинаково направленных сил
Этот метод, основанный на законе Гука, реализуется в пружинных весах и динамометрах. Закон Гука выполняется с определённой точностью и в определённых пределах деформаций. Другой метод определения сил основан на втором законе Ньютона (см. раздел динамики). Физической причиной воздействия на тело может быть вес тела, давление ветра, давление другого твёрдого тела, трение, электромагнитное воздействие и т.д. Но в механике абстрагируются от физической сущности воздействий, что позволяет рассматривать все их как силы. Линией действия силы называется прямая, вдоль которой направлена сила (прямая DE на рис. 1.1).
Рисунок 1.1 – Линия действия силы
Условимся еще о следующих определениях. 1. Системой силбудем называть совокупность сил, действующих на рассматриваемое тело (или тела). Если линии действия всех сил лежат в одной плоскости, система сил называется плоской, а если эти линии действия не лежат в одной плоскости, – пространственной. Кроме того, силы, линии, действия которых пересекаются в одной точке, называются сходящимися, а силы, линии действия которых параллельны друг другу, – параллельными. 2. Тело, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным. 3. Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными. 4. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешеннойили эквивалентной нулю. 5. Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующейданной системы сил. Сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающейсилой. 6. Силы, действующие на данное тело (или систему тел), можно разделить на внешние и внутренние. Внешниминазываются силы, которые действуют на это тело (или на тела системы) со стороны других тел, а внутренними–силы, с которыми части данного тела (или тела данной системы) действуют друг на друга. 7. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной. Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными. Понятие о сосредоточенной силе является условным, так как практически приложить силу к телу в одной точке нельзя. Силы, которые в механике рассматривают как сосредоточенные, представляют собой по существу равнодействующие некоторых систем распределенных сил. В частности, рассматриваемая в механике сила тяжести, действующая на данное твердое тело, представляет собой равнодействующую сил тяжести, действующих на его частицы. Линия действия этой равнодействующей проходит через точку, называемую центром тяжести тела. Задачами статики являются: 1) преобразование систем сил, действующих на твердое тело, в системы им эквивалентные, в частности приведение данной системы сил к простейшему виду; 2) определение условий равновесия систем сил, действующих на твердое тело. Решать задачи статики можно или путем соответствующих геометрических построений (геометрический и графический методы), или с помощью численных расчетов (аналитический метод). В курсе будет главным образом применяться аналитический метод, однако, следует иметь в виду, что наглядные геометрические построения играют при решении задач механики чрезвычайно важную роль.
Аксиомы статики.
1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F1=F2) и направлены вдоль одной прямой в противоположные стороны(рис. 1.2).
Действие данной системы сил на абсолютно твердое тело не изменяется, если к ней прибавить или от нее отнять уравновешенную систему сил. Иными словами это означает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу. Следствие: действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела. В самом деле, пусть на твердое тело действует приложенная в точке А сила Таким образом, вектор, изображающий силу
Рисунок 1.3 – Перенос силы вдоль линии действия Полученный результат справедлив только для сил, действующих на абсолютно твердое тело. При инженерных расчетах им можно пользоваться лишь тогда, когда определяются условия равновесия той или иной конструкции и не рассматриваются возникшие в ее частях внутренние усилия. Например, изображенный на рис. 1.4, а стержень АВ будет находиться в равновесии, если F1=F2. При переносе точек приложения обеих сил в какую-нибудь точку С стержня (рис. 1.4, б) или при переносе точки приложения силы
Рисунок 1.4 – Изменение внутренних усилий при переносе точек приложения сил
Следовательно, при определении внутренних усилий переносить точку приложения силы вдоль линии действия нельзя.
Закон равенства действия и противодействия: при всяком действии одного материального тела на другое имеет место такое же численно, но противоположное по направлению противодействие. Эта аксиома проиллюстрирована рисунком 1.7. Если тело А действует на тело В с силой
Рисунок 1.7 - Закон равенства действия и противодействия
Свойство внутренних сил. Любые две части тела (или конструкции) действуют друг на друга с равными по модулю и противоположно направленными силами. Так как при изучении условий равновесия тело рассматривается как абсолютно твёрдое, то все внутренние силы образуют при этом уравновешенную систему сил, которую можно отбросить. Следовательно, при изучении условий равновесия тела (конструкции) необходимо учитывать только внешние силы, действующие на это тело (конструкцию). В дальнейшем, говоря о действующих силах, мы будем подразумевать, если не сделано специальной оговорки, что речь идёт только о внешних силах. Принцип отвердевания. Если деформируемое тело находится под действием некоторой системы сил в равновесии, то равновесие не нарушится и в том случае, если это тело отвердеет (станет абсолютно твердым). Из принципа отвердевания следует, что условия равновесия, являющиеся необходимыми и достаточными для абсолютно твердого тела, являются необходимыми, но недостаточными для соответствующего деформируемого тела. Например, твердый брусок (рисунок 1.8, а, б) находится в равновесии под действием двух сил, равных по модулю и направленных вдоль оси бруска друг к другу либо друг от друга, а нить, соответствующая этому бруску, находится в равновесии только под действием двух сил, равных по модулю и направленных вдоль нити друг от друга (рисунок 1.9). Очевидно, что под действием сил, направленных друг к другу, нить сомнется.
Рисунок 1.8 – Равновесие жёсткого стержня при растяжении (а), и сжатии (б)
Рисунок 1.9 – Равновесие нити при растяжении
Закон параллелограмма сил: две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах. Вектор
Следовательно, закон параллелограмма сил можно еще сформулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.
В дальнейшем следует различать понятия суммы сил и их равнодействующей. Поясним это примером. Рассмотрим две силы
Рисунок 1.6 – Случай, когда сумма сил не является равнодействующей
Система сходящихся сил Сложение сил. Главным вектором системы сил называют геометрическую сумму сил системы. |
|
 ,
,  , приложенных в одной и той же точке в разное время, можно сравнивать численные значения этих сил:
, приложенных в одной и той же точке в разное время, можно сравнивать численные значения этих сил: .
.


 (рис. 1.3). Возьмем на линии действия этой силы произвольную точку В и приложим в ней две уравновешенные силы
(рис. 1.3). Возьмем на линии действия этой силы произвольную точку В и приложим в ней две уравновешенные силы  . От этого действие силы
. От этого действие силы 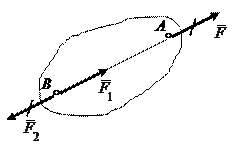
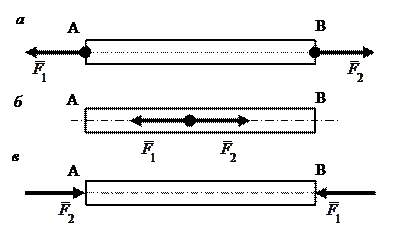
 , то одновременно тело В действует на тело А с силой
, то одновременно тело В действует на тело А с силой  . Нужно запомнить, что силы
. Нужно запомнить, что силы  и
и 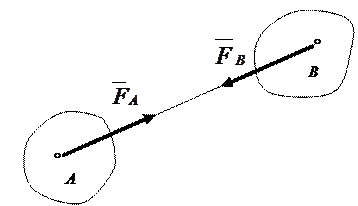


 , равный диагонали параллелограмма, построенного на векторах
, равный диагонали параллелограмма, построенного на векторах  .
.

 равна геометрической сумме сил
равна геометрической сумме сил  ), как диагональ соответствующего параллелограмма. Но сила
), как диагональ соответствующего параллелограмма. Но сила 