|
|
Электролитпен коагуляциялау кинетикасы 13 глава
Бұл теңдеудің дұрыс екені көптеген эксперименттер арқылы дәлелденді. Мысалы, Сведверг алтынның зольін микроскоп арқылы тексере отырып
формуласы бойынша теориялық жолмен есептеген мәнімен салыстырды. Мұндағы, Оның диаметрі 0,444 мк болатын бөлшекке алған мәліметтері төменде көреетілген:
Сведбергтің жүмыстарында осы теорияны тексеру арқылы алтынның кірнесі үшін Авагадро саны 6,2·10 23, ал сынаптың дисперстік бөлшектері үшін 5,9·1023-ке тең болғаны да бұл теорияның (формуланың) дұрыстығын көрсетті. Осыған ұқсас мәліметтер басқа зерттеушілердің жұмыстарынан көруге болады. Перрен және оның шәкірттері Шедесь, Добровский, Беррум гуммигут пен өсімдік смоласының (мастиктер) бөлшектерінің қозғалысын ультромикроскоп арқылы байқай отырып, Авогадро санын есептеді. Ол 6,03.·1023-ке тең болды. Бұл да қазіргі кезде қалыптасқан Авагадро санының мәніне (6,024·1023) өте жақын. Зеддиг те жоғарғы айтылған теңдеудің дұрыстығын Флуктуация дегеніміз-өте кіші көлемдегі кез-келген бір параметрдің өзінің тепе-теңдік мәнінен ауытқуы, Флуктуацияның жалпы теориясының негізін салған американ ғалымы Гиббс (1902ж.). Әрине коллоидтық химия курсында бұл теорияны толық қарастырудың қажеті жоқ. Оның коллоидтық жүйеге де қолданылатынын айтып кеткен жөн. Мысалы үшін коллоидтық жүйелерде микрокөлемдегі әртүрлі сандық концентрацияның ықтималдығын және осы көлемдегі қарастырылып отырылған концентрация қанша уақыт аралығында қайталатынын есептеуге флуктуация теориясын қолданады.
3.2 Коллоидтық жүйелердегі диффузия Диффузиямен біз жалпы химия курсында танысқанбыз. Диффузия деп-жүйедегі молекулалардың концентрациясының өз бетінше теңелу үдерісін айтатынбыз. Ал коллоидты-дисперстік жүйе мен ҮМҚ ертінділері үшін диффузия деп дисперстік фазаның бөлшектерінің, иә макромолекулалардың концентрациясының жылулық қозғалысының әсеріне дисперсиялық ортаның көлемінде өз бетінше теңелуін айтамыз. Егер концентрация жүйенің әр жерінде бірдей болмаса, онда жоғарғы концентрациялы жерден төменгі концентрациялы жерге қарай бөлшектердің ағыны пайда болады. Диффузия арқылы массаның тасымалдануы кәдімгі жылу мен электр тоғының тасымалдануына ұқсас, яғни жылудың ыстық денеден салқын денеге ауысатыны сияқты жоғарғы концентрациялы бөлшектер концентрациясы аз жаққа қарай ауысады. Осы ұқсастықты швециялық Фик пайдаланып 1855 ж. диффузияның заңын былай тұжырымдады:
Мұнда
х-тің өсуіне байланысты С азаятындықтан теңдікте оң жағындағы өрнектің алдына – таңбасы қойылған. Жоғарғы теңдікті былай да көрсетуге болады:
деп жазуға болады. Егер 1908 ж. Эйнштейн диффузия коэффиценті D, абсолюттік температура Т, дисперсиялық ортаның тұтқырлығы
3.2 - сурет. Эйнштейн теңдеуін қорытуды түсіндіретін сұлба
Бұл көлденең қимасы S см2 болатын ерітіндімен толтырылған түтікше. Онда солдан оңға қарай еріген заттың концентрациясы кемиді деп есептейік. Осы түтікшеден жұқа қалыңдықта ерітіндінің қабатын ойша бөліп алайық. Бұл жағдайда еріген затты тасымалдау бағыты стрелкамен көрсетілген, Диффузияланатын бөлшектің тұрақты жылдамдығы жылжу күші
Егер элементарлық қабаттағы еріген заттың молярлық концентрациясы c деп белгілесек, онда жеке бір бөлшекте қозғаушы күшті былайша жазуга болады:
Мұнда, R – газдың универсалдық тұрақтысы; Т –абсолюттік температура; NA – Авогадро саны.
Мұны теңдіктің екі жағынан
Мұндағы сu-деп отырғанымыз бірлік уақыт аралығындағы бірлік ауданнан диффузияланған заттың мөлшері, оны басқаша m деп керсетуге болады. Ендеше:
Ал Фик заңы бойынша осы жағдайда
Бұл теңдеуді Эйнштейн теңдеуі деп атайды. Шар тәрізді бөлшектер үшін
Ендеше:
Бұдан диффузия коэффиценті абсолюттік температураға тура, ал ортаның тұтқырлығы мен бөлшектің радиусына кері пропорционал екені көрініп тұр. Шындығында да диффузия бөлшектердің жылулық қозғалысының әсерінен болғандықтан, температура өскен сайын диффузия күшейеді. Ал неғұрлым бөлшек кіші болса, соғұрлым оның диффузиясы да күштірек болады. Жәй молекулаларға қарағанда коллоидтық бөлшектердің шамасы үлкен болғандықтан, олардың диффузия коэффиценті өте аз шама. Міне сондықтанда Грэм кезінде коллоидтық жүйеде диффузия болмайды деген теріс қорытындыға келген. Диффузия жылдамдығының коллоидтық бөлшектердің шамасына байланыстылығын бірінші рет 1869 ж. И.Г. Борщев керсеткен болатын. Егер Д, Т және
Осы формуладан r-ді тауып 1 моль заттың массасын былайша есептеуге болады:
3.3 Коллоидтық жүйелердегі осмостық құбылыс Осмостық құбылыстардың механизмдері мен негізгі заңдылықтары да диффузия сияқты жалпы химия мен физикалық химия курсында қарастырылған болатын. Сондықтан бұл жерде концентрациясы әртүрлі екі ерітіндіні жартылай өткізетін мембрана (жарғақ) арқылы бөлгенде еріткіштің концентрациясы аз ерітіндіден концентрациясы көп ерітіндіге қарай өтетінін еске алсақ жеткілікті. Шын ерітінділер үшін осмостық қысым Вант-Гоффтың теңдеуі бойынша мынаған тең:
Мұнда с-молярлық концентрация;
Осы теңдеуді коллоидтық жүйелерге қолдануға бола ма? Бұған жауап қайтару үшін дисперстік жүйенің концентрациясын анықтау керек. Біз кинетикалық құбылысты қарастырып отырғандықтан концентрация деп кинетикалық бірліктің-коллоидтық бөлшектердің бірлік көлемдегі (
Коллоидтық ерітінді үшін:
Мұнда Олай болса коллоидтық ерітінді үшін осмостық қысымды былайша жазатын боламыз:
Коллоидтық ертінділердің шын ертінділерден ерекшелігі оларда осмостық қысым мәні аз және тұрақсыз болады. Олай болу себебін мынадан көруге болады. Екі коллоидтық жүйені қарастырайық. Бірдей төмпературада біріншісінің осмостық қысымы
Бұл теңдікті бір-біріне бөліп, мына теңдікті шығаруға болады:
Бұдан дисперстік жүйелердің осмостық қысымдары тек сандық концентрациямен анықталғандығы және белшектердің шамасы мен табиғатына байланыссыз екендігі көрініп тұр. Коллоидтық жүйелерде белшектердің массасы көп болғандықтан бірдей салмақтық концентрацияда олардың сандық концентрация шын ерітінділерден әлдеқайда аз. Сол себепті осмостық қысымдары да аз болады. Міне Грэм диффузия сияқты коллоидтық жүйелерде осмос қысымдары болмайды деген қате пікірде болған. Өйткені оның қолданған осмометрі (осмос қысымын өлшейтін құрал) өте сезімтал емес еді. Дисперстік жүйелердегі осмостық қысымның тағы бір ерекшілігі - олардың тұрақсыздағы. Ол дисперстік жүйелерде болатын агрегация (өз бетінше бөлшектердің жылулық қозғалысының әсерінен соқтығысып бірігуі) құбылысына байланысты. Салмақтық концентрациясы С бірдей, бірақ бөлшектерінің шамасы әртүрлі екі коллоидтық ертінділер үшін мынаны жазуға болады:
Мұнда:
Бұл теңдеуге байланысты екі жұйенің осмостық қысымдарының қатынасы олардың бөлшектерінің радиустарының кубтарының қатынастарына кері пропорционал. Бұдан радиустарының аз ғана өзгеруінің өзі осмостық қысымның өте көп өзгеруін тудырады. Міне осы себепті дисперстік фазаның бөлшектерінің бірігуіне байланысты олардың қысымы өте күшті азаяды. Керісінше егер агрегат жеке бөлшектерге бөлінсе, онда ондай жүйелерде осмос қысымы көбейеді. Агрегация және дезагрегация құбылыстары сыртқы факторлардың әсерінен коллоидтық жүйелерде болғандықтан олардың осмостық қысымдары тұрақсыз болады. Міне осы айтылғандардың коллоидтық ертінділер мен шын ертінділердің осмос құбылысы үшін ешқандай да сапалық айырмашылығы болмайтынын олардың айырмашылығы тек сандық екенін айтуға болады. Оларда осмос құбылысының негізгі заңдылықтары бірдей, тек сандық концентрациялары әр түрлі болғандықтан коллоидтық жүйелерде осмос қысымы өте нашар болады. 3.4 Доннанның мембраналық тепе-теңдігі Диффузия, осмос және ультрафильтрация (ультрасүзілу) құбылыстарын зерттей отырып, көптеген зерттеушілер алғаш мембранадан кристаллоидтардың иондары емін еркін өтеді де,ал коллоидтық бөлшектер өтпейді деген ойда болған. Доннан зольдердің электролитпен бірге диализдегенде бұндағы құбылыстың күрделі екенін көрсетті. Электролит қосқан кезде оның иондары коллоидтық бөлшектердің иондарымен әрекеттесіп жүйеде мембраналық тепе-теңдік қалыптасады. Осыған байланысты коллоидтық жүйеде осмос қысымы коллоидтық бөлшектерге ғана емес олардың тепе-теңдікте болатын оған қосылған электролит иондарына да тәуелді болады. Бұл мембраналық тепе-теңдікті алғаш Доннан зерттегендіктен соның есімімен Доннанның мембраналық тепе-теңдігі деп те атайды. Осы мембраналық тепе-теңдіктің негізгі жағдайларын қарастырайық. Бір осмометрдің қабырғасы арқылы коллоидтық бөлшек өте алмайтындығын, ал электролит иондары емін-еркін өте алатындай болсын. Оның ішінде Na+катионы мен коллоидтық анионнан R- тұратын ерітінді болсын. Бұндағы Na+ мен R- концентрациясын С1 деп белгілеп, осмометрдің сыртында таза еріткіш емес, коллоидтық ерітіндімен ортақ ионы бар электролит болсын (мысалы, NaCl). Ал оның концентрациясын С2 деп белгілейік. Сұйылтылған, әрі күшті электролиттерге диссоциация толық жүретінін біле отырып, тепе-теңдікке дейін сырттан осмометрге өтетін электролит санын X деп белгілеп осмометрдің ішіндегі және сыртындағы иондардың концентрацияларын сұлбалық түрде былай көрсетуге болады.
р – осмостық қысым. Тепе-теңдікте болған жағдайда осмометрдегі қысым
оған қарама-қарсы қысым
Мұндағы
Егер мембраналық тепе-теңдікті есепке алмасақ, онда қарастырылып отырған коллоидтық ертіндінің осмостық қысымы
тең болады. Жоғарғы (4.3) теңдеуді (4.4) -теңдеуге бөлсек:
Бұл өрнек тепе-теңдік жағдайдағы осмостық қысым бастапқы жағдайдан қаншалықты өзгеретінін көрсетеді. Тепе-теңдік болу үшін мембранадан өте алатын иондардың концентрацияларының көбейтінділері сол мембрананың екі жағында да бірдей болу керек, яғни:
Бұдан х-тің мәнін былайша табуға болады:
Егер х-тің мәнін (5) теңдеуге қойсақ:
(4.8) - теңдеуден егер сырқы электролиттік концентрациясы өте аз болатын болса, яғни
Онда:
Ендеше
Мұндағы
Егер
яғни электролит мембрананың екі жағына бірдей белінеді. Егер |
|
 немесе
немесе 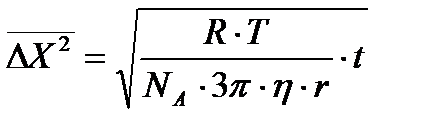
 -тің мәнін анықтап оны
-тің мәнін анықтап оны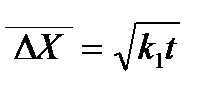
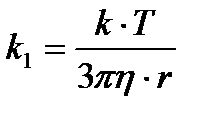
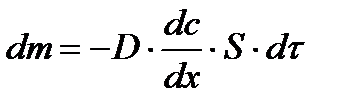
 – заттың диффузияланған шамасы (мөлшері); D – диффузия коэффиценті, бұл диффузия бөлшек пен ортаға байланысты болады.
– заттың диффузияланған шамасы (мөлшері); D – диффузия коэффиценті, бұл диффузия бөлшек пен ортаға байланысты болады. 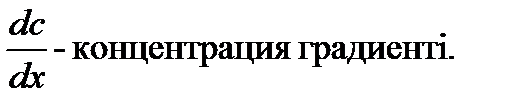
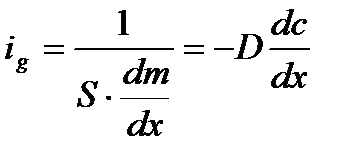
 – диффузияның меншікті ағыны дейді, өйткені ол бірлік уақыт ішінде, бірлік ауданнан тасымалданатын заттың мөлшерін (шамасын) көрсетеді. Диффузиялық ағын жалпы алғанда х пен
– диффузияның меншікті ағыны дейді, өйткені ол бірлік уақыт ішінде, бірлік ауданнан тасымалданатын заттың мөлшерін (шамасын) көрсетеді. Диффузиялық ағын жалпы алғанда х пен  функция болады. Өйткені х пен
функция болады. Өйткені х пен  концентрацияның градиентіне байланысты. Егер концентрацияның градиенті
концентрацияның градиентіне байланысты. Егер концентрацияның градиенті  тұрақты болса, онда диффузиялық ағын уақыттың өтуіне байланысы өзгермейді. Бұндай жағдайда,
тұрақты болса, онда диффузиялық ағын уақыттың өтуіне байланысы өзгермейді. Бұндай жағдайда,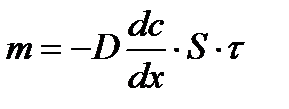
 ;
;  және
және  болса,
болса,  яғни диффузия коэффиценті сан жағынан бірлік уақыт аралығында бірлік ауданнан тасымалданатын бірлік дененің шамасын керсетеді.
яғни диффузия коэффиценті сан жағынан бірлік уақыт аралығында бірлік ауданнан тасымалданатын бірлік дененің шамасын керсетеді. және дисперстік фазаның бөлшектерінің радиусымен r байланыстыратын теңдеу қорытып шығарды. Теориялық және практикалық маңызы бар бұл теңдеуді қорыту үшін 3.2 - суретте керсетілген сүлбаға тоқталайық.
және дисперстік фазаның бөлшектерінің радиусымен r байланыстыратын теңдеу қорытып шығарды. Теориялық және практикалық маңызы бар бұл теңдеуді қорыту үшін 3.2 - суретте керсетілген сүлбаға тоқталайық. пен
пен  жазықтарымен шектелген бұл элементарлық қабаттың көлемі
жазықтарымен шектелген бұл элементарлық қабаттың көлемі  - ке тең болады. Енді осы қабаттың сол жағындағы ерітіндінің концентрациясы мен осмостық қысымын
- ке тең болады. Енді осы қабаттың сол жағындағы ерітіндінің концентрациясы мен осмостық қысымын  және
және  деп, ал оң жағындағысын сәйкес
деп, ал оң жағындағысын сәйкес  және
және  белгілейік. Әрине
белгілейік. Әрине  және
және  .
.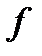 пен бөлшекке кедергі жасайтын қозғау күшіне қарама-қарсы бағытталған кедергі күші
пен бөлшекке кедергі жасайтын қозғау күшіне қарама-қарсы бағытталған кедергі күші  өзара тең болғанда ғана жүзеге асады, яғни
өзара тең болғанда ғана жүзеге асады, яғни  . Кедергі күші
. Кедергі күші  кедергі козффиценті В мен бөлшектің қозғалу жылдамдығының көбейтіндісіне тең
кедергі козффиценті В мен бөлшектің қозғалу жылдамдығының көбейтіндісіне тең  .Ал кедергі коэффиценті болса, бұрын айтылғандай, шар тәрізді бөлшектер үшін
.Ал кедергі коэффиценті болса, бұрын айтылғандай, шар тәрізді бөлшектер үшін 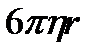 ге тең. (мұнда
ге тең. (мұнда 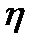 - дисперсиялық ортаның тұтқырлығы, r-бөлшектің радиусы). Бір ғана бөлшекке әсер ететін қозғау күшін есептеу үшін алдымен элементарлық қабаттың бірлік көлеміне әсер ететін қозғау күшін F анықтайды. Ол:
- дисперсиялық ортаның тұтқырлығы, r-бөлшектің радиусы). Бір ғана бөлшекке әсер ететін қозғау күшін есептеу үшін алдымен элементарлық қабаттың бірлік көлеміне әсер ететін қозғау күшін F анықтайды. Ол: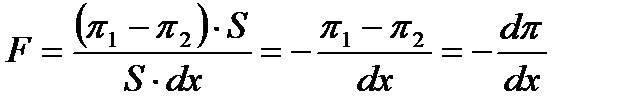

 Осылардың орнына мәндерін қойсақ:
Осылардың орнына мәндерін қойсақ: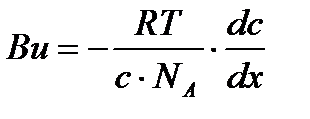
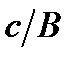 көбейтіп былай жазуға болады:
көбейтіп былай жазуға болады:
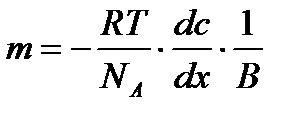
 Бұл екі теңдікті теңестірсек:
Бұл екі теңдікті теңестірсек: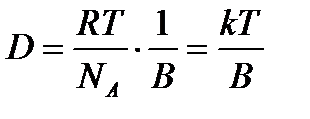
 .
.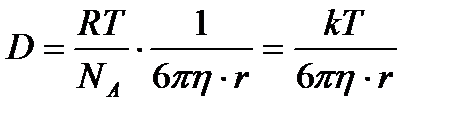
 мәндері белгілі болса, (олар қарастырып отырған жүйеде тұрақты шамалар) онда Эйнштейн теңдеуін пайдаланып, 1 моль заттың массасын анықтауға болады. Жоғарғы теңдік бойынша:
мәндері белгілі болса, (олар қарастырып отырған жүйеде тұрақты шамалар) онда Эйнштейн теңдеуін пайдаланып, 1 моль заттың массасын анықтауға болады. Жоғарғы теңдік бойынша: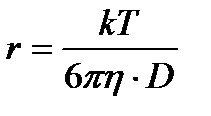
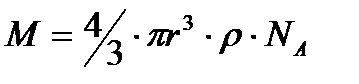
 – дисперстік фазаның тығыздығы (ол да белгілі бір диффузия үшін тұрақты, белгілі шама). Сонымен диффузия коэффицентін біле отырып, бір моль заттың молекулалалық салмағын табуға болады екен.
– дисперстік фазаның тығыздығы (ол да белгілі бір диффузия үшін тұрақты, белгілі шама). Сонымен диффузия коэффицентін біле отырып, бір моль заттың молекулалалық салмағын табуға болады екен.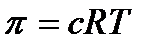
 -осмостық қысым.
-осмостық қысым. ) санын айтамыз. Ендеше коллоидтық жүйелер үшін молярлық концентрация емес, сандық концентрация қолданады.
) санын айтамыз. Ендеше коллоидтық жүйелер үшін молярлық концентрация емес, сандық концентрация қолданады.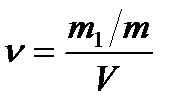
 -сандық концентрация;
-сандық концентрация;  – еріген заттың массасы;
– еріген заттың массасы;  – бөлшектің массасы; V – жүйенің көлемі.
– бөлшектің массасы; V – жүйенің көлемі.
 ,ал екіншісінікі
,ал екіншісінікі  болсын.
болсын.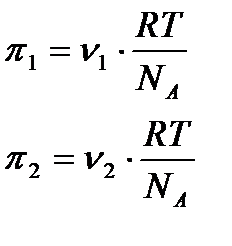
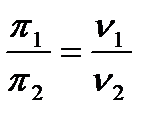


 бірінші және екінші ертіндідегі бөлшектердің радиусы.
бірінші және екінші ертіндідегі бөлшектердің радиусы.  – дисперстік фазаның тығыздығы.
– дисперстік фазаның тығыздығы.


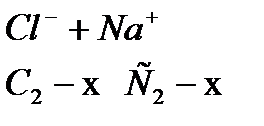
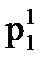 мынаған тең:
мынаған тең: (4.1)
(4.1) :
: (4.2)
(4.2) деп отырғанымыз осмометрмен өлшенетін осмостық қысым
деп отырғанымыз осмометрмен өлшенетін осмостық қысым  :
: (4.3)
(4.3) (4.4)
(4.4) (4.5)
(4.5) немесе
немесе  (4.6)
(4.6) (4.7)
(4.7) (4.8)
(4.8) , оны елемей
, оны елемей  деп жазуға болады, яғни бақылап отырған осмостық қысымына тең. Егер
деп жазуға болады, яғни бақылап отырған осмостық қысымына тең. Егер  , болса, онда зольдің концентрациясын елемеуге болады.
, болса, онда зольдің концентрациясын елемеуге болады.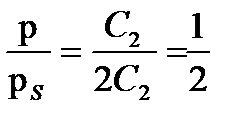 (4.9)
(4.9) яғни бұл кірненің шын қысымы бақылап отырған қысымнан екі есе көп болады. Осы қарастырып отырған екі шекті жағдайдың аралығында болатын электролиттің әр түрлі концентрациясына мынаны жазуға болады:
яғни бұл кірненің шын қысымы бақылап отырған қысымнан екі есе көп болады. Осы қарастырып отырған екі шекті жағдайдың аралығында болатын электролиттің әр түрлі концентрациясына мынаны жазуға болады: (4.10)
(4.10) мына аралықта өзгереді:
мына аралықта өзгереді: 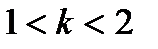 (6) - теңдеу мембрананың екі жағында бірдей ион болмаған жағдайларда қолдануға болатынын Доннан көрсеткен болатын.Осыдан диализ кезінде кірнеге электролиттік қаншалықты мөлшерде тасымалданатынын былайша жазамыз: (х - ты С - ге бөлсек осы өрнек алынады)
(6) - теңдеу мембрананың екі жағында бірдей ион болмаған жағдайларда қолдануға болатынын Доннан көрсеткен болатын.Осыдан диализ кезінде кірнеге электролиттік қаншалықты мөлшерде тасымалданатынын былайша жазамыз: (х - ты С - ге бөлсек осы өрнек алынады) (4.11)
(4.11) - электролиттің кірнеге өткен бөлігін көрсетеді.
- электролиттің кірнеге өткен бөлігін көрсетеді. , болса, онда С-ді елемей мынаны жазуға болады.
, болса, онда С-ді елемей мынаны жазуға болады. (4.12)
(4.12) болса, онда
болса, онда  бұдан электролиттің концентрациясы өте аз болғанда ол мембрананың сыртында болатыны керініп тұр. Доннанның мембраналық теп-теңдігінің көптеген құбылыстарды (мысалы, лиофобты коллоидтық және ҮМҚ ерітінділерінің осмос қысымын, ісіну құбылыстарын, иондардың теріс адсорбциясын және әр түрлі физиологиялық қубылыстарды) түсіндіруде теориялық маңызы зор.
бұдан электролиттің концентрациясы өте аз болғанда ол мембрананың сыртында болатыны керініп тұр. Доннанның мембраналық теп-теңдігінің көптеген құбылыстарды (мысалы, лиофобты коллоидтық және ҮМҚ ерітінділерінің осмос қысымын, ісіну құбылыстарын, иондардың теріс адсорбциясын және әр түрлі физиологиялық қубылыстарды) түсіндіруде теориялық маңызы зор.