|
|
Электролитпен коагуляциялау кинетикасы 14 глава
3.5 Седиментация. Седиментациялық-диффузиялық тепе-теңдік Біз диффузияны қарастырғанда жүйеге жердің тарту күшінің әсерін елеген жоқ болатынбыз. Егер жүйеде бөлшектер ірірек болатын болса, жердің тарту күшін елемеу дұрыс емес, өйткені гравитацияяық күштің әсерінен бөлшектер шөге бастайды, яғни седиментацияланады. Егер бөлшектер ауыр болса, олардың бәрі тұнбаға түседі, егер жеңілірек болса, жүйеде бөлшектердің биіктікке байланысты бөлініп белгілі бір тепе-теңдік сақталады. Дисперстік жүйенің барлық көлем бойынша бөлшектердің бір қалыпты бөліну қалпын сақтау қабілеті жүйенің седиментациялық, иә кинетикалық тұрақтылығы деп аталады (кинетикалық түрақтылық дегенді Песков енгізген болатын). Бүл тұрақтылық дербес дисперстік жүйелер үшін қарастырылатынын айтқан жөн. Егер белшектер өте үлкен болса, дөрекі дисперстік жүйелер, (мысалы, шаң, құмның судағы жүзгіні т.б.) кинетикалық тұрақсыз болады, өйткені олар броундық қозғалыста болмай өз салмақтарының әсерінен тұнбаға түседі. Ал жоғарғы дисперстік жүйелер (газдар, шын ерітінділер) кинетикалық тұрақты, өйткені жылулық қозғалыс оларға тән қасиет, сондықтан олардың диффузиялық қабілеттілігі болады. Коллоидтық жүйелер аралық жағдайда болады. Олардағы бөлшектерге гравитациялық күш әсер етеді және олар жылулық қозғалыстың әсерінен диффузияға да бейім. Міне сондықтан диффузиямен бөлшектердің салмақ күштерінің әсерінен көлемнің биіктігі бойынша бөлшектердің әр текті бөлініуінен жүйеде тепе-теңдік орнайды. Бұл тепе-теңдікті седиментациялық-диффузиялық тепе-теңдік деп атайды. Тепе-теңдік жағдайда бөлшектердің биіктік бойынша бөліну заңы Лапластың газдардың атмосферада барометрлік (немесе биіктікке байланысы гипсометрлік) заңына ұқсас:
С1 - алғашқы деңгейдегі жүйенің концентрациясы; С2 - һ биіктігіндегі концентрациясы; М- заттың (1 моль) массасы; g - еркін түсу үдеуі.
Бұл формуланы термодинамикалық жолмен де кинетикалық жолмен де қорытуға болады. Орыс тілінде жазылған көптеген оқулықтарда көбінде термодинамикалық жолмен қорыту жазылғандықтан, біз тек кинетикалық жолмен қорытуға тоқталайық, Больцман заңы бойынша мынаны жазуға болады:
Е-нің шамасы 0-деген индекс дисперсиялық ортаны көрсетеді. Олардың мәнін қойсақ:
Бұл теңдіктердіктерді бір-біріне бөліп және:
екенін еске ала отырып шыққан нәтижені логарифмдесек мына теңдеу шығады:
Бұл теңдеудің тарихи маңызы бар. Осы теңдеу бойынша молекулалы-кинетикалық теорияның ең қажетті тұрақтыларының бірі – Авогадро санының мәні есептелген. Оны өзінің классикалық жұмыстарында гуммигит бөлшектерінің радиусын біле отырып, әртүрлі деңгейдегі бөлшектер санын микроскоп арқылы санап, Перрен жоғарғы теңдеу бойынша бірінші рет Авогадро санын есептеу арқылы шығарды. Ол 6,7·1023-ке тең, яғни қазіргі мәніне жақын. Седиментациялық-диффузиялық тепе-теңдікті ең бірінші Перрен NА есептеу үшін қолданғандықтан, ал формула Больцман заңымен қорытылғандықтан кейде Перрен-Больцманның седиментациялық -диффузиялық тепе-теңдігі деп атайды. Перреннің бұл жұмысы молекулалы-кинетикалық теорияның заңдарын коллоидтық жүйелер үшін де қолдануға болатындығын көрсетті. Вестгрен де алтынның зольдерімен жұмыс істей отырып, жоғарғы формула бойынша Авогадро санын есептеді. Ол 6,5·1023 -не тең болды. Ірі дисперстік жүйелерде қарастырылып отырған белшектеріміздің тығыздығы ортаның тығыздығынан жоғары болғандықтан олардың броундық қозғалыстан жылжуынан гөрі ауырлық күшінің әсерінен шөгуі өте жылдамырақ болады. Шөгу (седиментациялық) жылдамдықты өлшеу арқылы бөлшектердің шамасын (радиусын) табуға болады. Осыған негізделген тәсілді седиментациялық талдау дейді. Шөгетін бөлшектерге екі түрлі күш әсер етеді. Біріншісі: бөлшектердің ауырлық күші –
Егер бөлшек шар тәрізді болса,
Егер бөлшектерге тек ғана Үйкелу күші Стокс заңы бойынша мынаған тең:
Мұнда, В – бөлшек пен ортаның үйкелу коэффиценті; u – бөлшектің седиментациялық жылдамдығы; В – шар тәрізді бөлшектер үшін
Бұдан бөлшектердің седиментациялық жылдамдығын оңай табуға болады:
Бұдан бөлшектердің седиментациялық жылдамдықтарын олардың радиустарына (иә диаметріне) тура, ал ортаның тұтқырлығына кері пропорционал екенін көруге болады. Егер
Бұл өрнектегі u басқа шамалардың бәрі берілген дисперсиялық орта мен дисперстік фаза үшін тұрақты болғандықтан басқаша оны былайша жазуға болады:
мұндағы
Егер монодисперстік жүйені қарастырсақ, онда шөгетін бөлшектердің шамасы бірдей болғандықтан, бөлшектердің жүрген жолы (Н) уақытқа (
Ал бөлшектердің радиусын:
Мұндағы k-ның мәні жоғарыда көрсетілген. Міне бұл формула бойынша жүзгіннің бөлшектерінің радиусын олардың шөгуін қарапайым көзбен де, микроскоппен байқап отырып та есептеуге болады. Ал жүйе полидисперсті болса, онда шөгетін бөлшектердің радиустары әртүрлі болғандықтан шөгетін бөлшектердің қабатының шекарасы жақсы білінбейді. Өйткені әртүрлі бөлшектер бірдей уақыт аралығында әртүрлі жол жүріп өтеді.
3.6 Дисперстік жүйелерді седиментациялық талдау Кәдімгі жүзгіндер мен майғындар өлшемдері әртүрлі бөлшектерден тұратын жүйелер, яғни олар полидисперстік жүйелерге жатады. Седиментациялық талдаудың мақсаты – дисперстік жүйелердегі ең үлкен және ең кіші бөлшектердің өлшемдерін және жүйенің фракциялық құрамын анықтау болып саналады. Седиментациялық талдауды әртүрлі әдіспен жүргізуге болады. Олардың ішіндегі кең таралғандары сұйықтықтағы дисперстік бөлшектердің шөгу жылдамдықтарын анықтау қағидасына негізделген. Бұл принцип бойынша бөлшектердің шөгу жылдамдықтарын мынадай әдістердің көмегімен анықтауға болады: 1) микроскоптың көмегімен жүзгін бөлшектерінің шөгу жылдамдығын тікелей анықтау арқылы (микроскопиялық әдіс); 2) тұнбаның ыдыс түбіне немесе таразының табақшасына шөгу жылдамдығын анықтау арқылы (салмақтық әдіс); 3) шөгу құбылысы барысында дисперстік фазаның белгілі бір тереңдіктегі концентрациясының өзгерісін анықтау арқылы (көлденең сызық әдісі); 4) шөгу құбылысы барысында гидростатикалық қысымның өзгерісін анықтау арқылы; 5) шөгу құбылысы барысында дисперстік жүйе тығыздығының өзгерісін анықтау арқылы. Бұлардың ішіндегі ыңғайлылары, сондықтан жиі қолданылатындары, екінші мен төртінші әдістер.Жүзгіндегі дисперстік фаза бөлшектерінің шөгу жылдамдығын шөккен тұнба массасының уақыт бойынша өзгерісін таразының көмегімен тікелей өлшеу арқылы, немесе Фигуровскийдің седиментациялық таразысы көмегімен анықтауға болады. 3.6.1. Иін таразысы арқылы седиментациялық талдау жүргізу Седиментациялық талдау жасау үшін көбінесе иін (торзиондық) таразысын (3.3-сурет) қолданады. Жұмыс істеу тәртібі. Иін таразысын төменгі жағындағы бұрандалары (1 және 2) арқылы вертикаль жағдайға келтіреді. Арретирді (3) оңға бұру арқылы таразыны іске қосады. Сонан соң рычагты (4) жылжытып, шкала көрсеткішін (5) нөлге келтіреді. Сонда тепе-теңдік көрсеткіші (8) нольдік белгімен (9) сәйкес келуі тиіс. Егерде сәйкес келмесе, онда бұранда (6) арқылы тепе-теңдік көрсеткішті нольдік белгімен сәйкестендіреді. Арретирді солға жылжыту арқылы таразыны өшіреді. Сонан соң цилиндр ыдыс (10) (көлемі 1,0 л) алып, оған су құяды. Жұқа шыны түтікшеге бекітілген табақшаны (11) цилиндрдегі суға батырып, таразы иініне (7) іледі. Сонда цилиндрдің түбінен табақшаға дейінгі қашықтық 2÷3 см, табақшамен судың деңгейі арасындағы қашықтық 10÷12 см-ден кем болмауы, ал цилиндр қабырғасы мен табақша арасындағы кеңістік 2÷3 см болуы тиіс. Сонан соң арретирді оңға жылжытып, таразыны іске қосады да, рычагты қозғалту арқылы тепе-теңдік көрсеткішті нөлдік белгімен сәйкестендіреді. Арретирді солға жылжытып, таразыны өшіреді де, шкала көрсеткіші (5) арқылы табақшаның судағы массасын (р0), сонан соң табақша мен судың деңгейі арасындағы қашықтықты (Н) жазады. Табақшаны судан шығарып алып, цилиндрдегі суға зерттейтін үлгінің белгілі массасын (0,2 ÷ 0,5 мас. % -дық суспензия даярлау үшін қажетті) қосады. Басына резина диск бекітілген шыны таяқша көмегімен вертикаль бағытта қозғай отырып суспензияны 3 ÷ 5 минут бойы араластырады. Ары қарай табақшаны суспензияға батырып, таразы иініне жылдам іледі де, секундомерді қосады. Табақша тербелісі тоқтағаннан кейін (10 ÷ 15 секундтан соң) арретирді оңға жылжытып таразыны іске қосады да, табақшаға отырған тұнбаның массасын өлшей бастайды.
Бастапқы кезде тұнба массасын жиі (әрбір 30 с сайын) анықтайды, сонан соң уақыт аралығын ұлғайта түседі. Өлшеуді суспензиядағы дисперстік бөлшектер толығымен шөккенше, немесе тұнбаның массасы 30 минут бойы өзгермейтін жағдайға жеткенше жүргізеді. Тәжірибе барысында алынған мәндерді 3.1-кесте түрінде жазған ыңғайлы.Тәжірибелік мәндерден седиментация қисығын-тұнбаның салыстырмалы массасының уақытқа байланысты өзгерісін р(%)= f(t), тұрғызады. 3.1-кесте. t=… 0C; d =…кг/м3; d0= кг/м3; р0=… кг; h=… Па·с; Н=… м.
3.6.2 Фигуровскийдің таразысы арқылы седиментациялық талдау жүргізу Жоғарыда айтылғандай, суспензия бөлшектерінің дисперсиялық ортада шөгу жылдамдығын анықтау үшін Фигуровскийдің седиментациялық таразысын пайдалануға болады. Фигуровскийдің седиментациялық таразысы 3.4-суретте көрсетілген. Ол ұшы тартылып жұқартылған шыны түтікшеден (1) және жұқа шыны түтікше (3) арқылы ілінген табақшадан (2) тұрады. Айта кететін жай шыны түтікшенің деформациясы Гук заңына бағынуы, яғни DL = G×Dp теңдеуі орындалуы тиіс. Мұндағы Dp-тұнба массасының өзгерісі; G-серпімділік (Гук) коэффициенті; DL–деформация шамасы. Табақшаны суспензияға батырғанда, оның бетіне дисперстік фазаның бөлшектері отырады да, соның нәтижесінде шыны түтікше төмен қарай майысып, деформацияланады. Шыны түтікшенің деформациясын микрошкаламен жабдықталған микроскоп окуляры арқылы өлшеуге болады. Түтікше деформациясының уақытқа байланысты өзгерісін график түрінде өрнектесек, ол тұнба массасының (Dр) уақытқа (t) байланысты өзгерісі болып саналады. Өйткені Гук заңына сәйкес тұнба массасы мен түтікше деформациясы арасында тура байланыс бар. Фигуровский таразысының артықшылығы, ол арқылы сұйық суспензиядағы (0,01 ÷ 0,2%) шөгу құбылысын зерттеуге және бөлшектің шөгу биіктігін (Н) өзгертуге болады. Седиментациялық талдау жүргізу реті. Штативке шыны түтікшені (1) бекітіп, оның астына дисперстік ортамен (сумен) толтырылған цилиндрді (4) қояды. Сонан соң шыны табақшаны (2) дисперсиялық ортаға батырып, оны түтікшенің ұшына іледі. Ары қарай штативке бекітілген микроскоп окулярынан шыны түтікшенің ұшын (белгіні) іздеп табады. Белгі окулярдағы микрошкаланың төменгі жағында болуы керек, өйткені окуляр кері көріністі көрсетеді, деформация нәтижесінде окулярдағы белгі жоғары қарай көтеріледі. Шыны табақша таза дисперстік ортада болғандағы белгінің окулярдағы орны деформацияланудың бастапқы нүктесі L0 ретінде алынады. Сонан соң шыны табақшаны алып, цилиндрге зерттейтін дисперстік фазаның ұнтағын (0,2÷0,5 мас. %-дық суспензия алу үшін) қосады. Жүзгінді 3÷4 минут бойы басына резина диск бекітілген шыны таяқшаны жүзгінде вертикаль бағытта қозғалта отырып араластырады. Араластырып болған соң, табақшаны жүзгінге батырады да, шыны түтікшенің (1) ұшына іліп, секундомерді қосады. Табақша тербелісі тоқтағаннан кейін (10÷13 секундтан соң) окулярдан деформация шамасының уақыт бойынша өзгерісін анықтауға кіріседі. Бастапқы кезде деформация шамасын жиі (әрбір 30 с сайын) анықтайды да, сонан соң өлшеу уақыты аралығын ұлғайта түседі. Бақылауға жүзгіндегі дисперстік фазаның бөлшектері толығымен шөккенше, немесе деформация шамасы жарты сағат бойында өзгермейтін жағдайға жеткенше жүргізеді. Седиментациялық талдау жүргізу барысында төмендегі шарттардың орындалуын қадағалау қажет: 1) жүзгіннің температурасы тұрақты болуы; 2) тәжірибе барысында дисперсиялық ортаның буланбауы және шыны табақшаның астында газ көпіршіктері болмауы тиіс. Өйткені газ көпіршіктері табақшаны көтеріп, деформация мәнін өзгертуі ықтимал. Тәжірибе жүзінде алынған мәндерді 3.2-кесте түрінде жаз-ған ыңғайлы. Тәжірибелік мәндерден седиментация қисығын-тұнбаның салыстырмалы массасының уақытқа байланысты өзгерісін р (%)= f(t) тұрғызады.
3.2-кесте. t=…0C; d=…кг/м3; d0=кг/м3; h(Н2О)=…Па·с; Н= …м; L0=…
3.6.3 Седиментация қисықтары және оларды өңдеу Кез келген уақыт аралығындағы жүзгінде шөккен бөлшектердің радиусын есептеуге болады. Алайда жүйенің дисперстік құрамын анықтау үшін ондағы бөлшектердің радиустарын білу жеткіліксіз. Ол үшін жүйедегі өлшемдері әртүрлі бөлшектердің массалық үлесін де білу қажет. Жүйенің дисперстік құрамын седиментация қисығынан анықтауға болады. Седиментация қисығы шөккен бөлшектердің массасының, дәлірек айтқанда, салыстырмалы массасының уақытқа байланысты өзгерісін (р=f(t) тәуелдігі) сипаттайды. Шыны түтікшенің деформациясы тұнбаның массасына тура пропорционал болғандықтан, Фигуровский таразысының көмегімен алынған тәжірибелік мәндерден седиментация қисығын деформация шамасының уақытқа байланысты өзгерісін (DL=f(t)) тұрғызу арқылы алуға болады. Өйткені салыстырмалы деформацияның шамасы тұнбаның салыстырмалы массасына тура пропорционал: L(%) = f (p (%). Седиментация қисығының түрі жүзгіннің дисперстік құрамына байланысты әртүрлі болып келеді. Мысалы, монодисперстік (бөлшектерінің радиустары бірдей) жүйенің седиментация қисығы түзу сызықты болып келеді (3.5-суреттегі ОА және ОВ түзулері). Монодисперстік жүзгіндегі дисперстік бөлшектердің шөгу жылдамдықтары бірдей болғандықтан, тұнба жиналуының жалпы жылдамдығы тұрақты болады: (dp/dt)=const
Ал t1 және t2 уақыттарда монодисперстік жүйелердегі дисперстік бөлшектер толығымен шөгіп болады. Сонда бұл жүйелердегі дисперстік бөлшектердің шөгу жылдамдықтары мынаған тең болады: u1 = H/t1; u2 = H/t2
Мұндағы Н-бөлшектің шөгу биіктігі. Екі монодисперстік фракциялардан құралған бидисперстік суспензияның седиментация қисығы күрделілеу болып келеді (3.5-сурет, с түзуі).
3.5-сурет. Монодисперстік (а және в) және бидисперстік (с) жүйелердің седиментация қисықтары
Бидисперстік жүзгіндегі радиустары үлкенірек бөлшектер t1 уақытта толығымен шөгіп болады да, одан ары қарай радиустары кішірек бөлшектер шөгеді. В¢ нүктесінде екінші фракция бөлшектері толығымен шөгіп бітіп, одан ары қарай тұнбаның салмағы тұрақты болып қалады. Бидисперстік жүзгіннің жалпы седиментация қисығынан жеке фракциялардың седиментация қисықтарын тұрғызуға болады. Ол үшін жалпы седиментация қисығының А¢В¢ кесіндісін ордината өсімен қиылысқанша созып, сонан соң р2 нүктесінен А¢А¢¢ түзуімен қиылысқанша абсцисса өсіне параллель түзу жүргізу керек. Сонда А нүктесі ірі бөлшектерден тұратын фракцияның соңғы седиментация нүктесі болып табылады. А нүктесінен координатаның басына дейін түзу жүргізіп, ірі бөлшектерден құралған фракцияның седиментация түзуін (ОА) алуға болады. Ал координатаның бас нүктесінен р2А¢ түзуіне параллель түзу (ОВ) жүргізе отырып, ұсақ бөлшектерден құралған фракцияның соңғы седиментация нүктесін (В) табамыз. Сондағы р1 мен р2 шамалары жеке фракциялардың жүзгіндегі пайыздық мөлшерін көрсететін болғандықтан, р3 екі фракцияның жалпы массасына (100%) тең болады. Олай болса Ор2 мен р2р3 мәндері жүзгіндегі екі фракцияның пайыздық мөлшерін көрсетеді. Бидисперстік жүзгіннің фракцияларындағы бөлшектердің радиустарын олардың шөгу жылдамдықтарын (u1 мен u2) (6.7)-теңдеуге қойып есептейді. |
|
 немесе
немесе  (5.1)
(5.1) (5.2)
(5.2)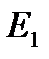 - моль заттың гравитациялық потенциалы 1 және 2 деген деңгейлер, төменгі және жоғарғы, немесе потенциалдық энергия.
- моль заттың гравитациялық потенциалы 1 және 2 деген деңгейлер, төменгі және жоғарғы, немесе потенциалдық энергия. мұндағы m бөлшекгің тиымдылық массасы деп аталынады. Архимед заңын еске алсақ:
мұндағы m бөлшекгің тиымдылық массасы деп аталынады. Архимед заңын еске алсақ:  (5.3)
(5.3)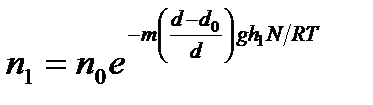
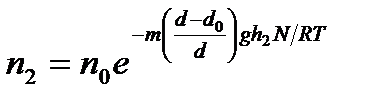 (5.4)
(5.4)
 (5.5)
(5.5) ; Архимед заңын еске ала отырып
; Архимед заңын еске ала отырып  -ді былай жазуға болады:
-ді былай жазуға болады: (6.1)
(6.1)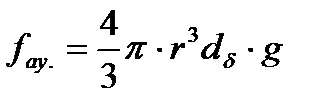 (6.2)
(6.2) (6.3)
(6.3)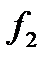 . Ол бағыты жағынан
. Ол бағыты жағынан  ) өзара теңеседі де, бөлшектер бірқалыпты қозғалады.
) өзара теңеседі де, бөлшектер бірқалыпты қозғалады. (6.4)
(6.4) ;
;  -ортаның тұтқырлығы; r –бөлшектердің радиустары.
-ортаның тұтқырлығы; r –бөлшектердің радиустары. (6.5)
(6.5) (6.6)
(6.6)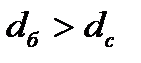 болса, онда бөлшектердің шөгуін, ал егер
болса, онда бөлшектердің шөгуін, ал егер 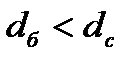 болса, онда бөлшектердің дисперсиялық ортаның бетіне қалқып шығуын байқауға болады. (мысалы, парафиннің судағы жүзгіні). Соңғы теңдіктен бөлшектердің (шамасын) радиусын былайша табамыз:
болса, онда бөлшектердің дисперсиялық ортаның бетіне қалқып шығуын байқауға болады. (мысалы, парафиннің судағы жүзгіні). Соңғы теңдіктен бөлшектердің (шамасын) радиусын былайша табамыз: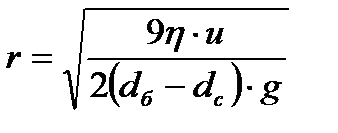 (6.7)
(6.7)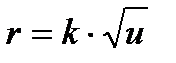 (6.8)
(6.8) (6.9)
(6.9) ) тура пропорционалды түрде өседі. Ендеше шөгу жылдамдығын былайша жазуға болады:
) тура пропорционалды түрде өседі. Ендеше шөгу жылдамдығын былайша жазуға болады: (6.10)
(6.10)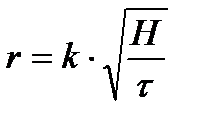 (6.11)
(6.11)