|
|
Электролитпен коагуляциялау кинетикасы 15 главаҮш және төрт дисперстік жүзгіндердің седиментация қисықтарын да дәл осылай талдауға болады. Күнделікті өмірде кездесетін жүзгіндер полидисперстік болып саналады. Полидисперстік жүзгіндердің седиментация қисығы пішіні жағынан гиперболаға жуық, бірқалыпты өсетін қисық болып келеді (3.6-сурет). Седиментация қисығында екі нүктені (А мен G) белгілеуге болады. А нүктесіне дейін тұнбаның мөлшері түзу сызықтың бойымен өседі де, G нүктесінен кейін тұнбаның мөлшері өзгеріссіз, тұрақты болып қалады. ОА түзуі ең ірі бөлшектердің шөгуіне сәйкес келеді. А нүктесінен абсцисса өсіне түсірілген перпендикуляр ең ірі бөлшектердің шөгу уақытын (tmin) береді. G нүктесінен түсірілген перпендикуляр жүзгіндегі ең ұсақ бөлшектердің шөгуінің аяқталу уақытын (tmax) көрсетеді. Сонда ең ірі және ең ұсақ бөлшектердің радиустары мынаған тең болады:
tmin уақытқа дейін тұнбаның жиналу жылдамдығы тұрақты: (dp/dt) = const. Ал tmin уақыттан бастап тұнбаның жиналу жылдамдығы өзгеріп отырады. Жүзгіндегі ең ірі және ең ұсақ бөлшектердің радиустарын анықтағаннан кейін, берілген полидисперстік жүйені формальды түрде бірнеше аралық фракцияларға бөліп қарастырады. Ол үшін седиментация қисығының бойынан бірнеше нүктелер (В, С, D, E және F) белгілейді. Бұл нүктелерге t1, t2, t3, t4, және t5 уақыттар сәйкес келеді де, осы уақыттарда шөккен бөлшектердің радиустары төмендегі теңдеу арқылы есептеледі:
Мұндағы К - шамасы (6.9)-теңдеу арқылы анықталады.
3.6-сурет.Полидисперстік жүзгіннің седиментация қисығы Егерде таңдап алынған нүктелер арқылы седиментация қисығына жанамалар жүргізіп, оларды ордината өсімен қиылысқанша созатын болсақ,
Мұндағы:
(6.14) - теңдеуді Оден теңдеуі деп атайды. Бұл теңдеудегі ti Жүзгіннің дисперстік құрамын анықтау үшін интегралдық және дифференциалдық қисықтарын тұрғызады. Интегралдық қисығын тұрғызу үшін седиментация қисығынан радиусы ri-ден үлкен дисперстік бөлшектерден тұратын фракцияның суспензиядағы пайыздық үлесін табады. Ол Дифференциалдық қисығын седиментация мен интегралдық қисықтарынан тұрғызуға болады. Ол үшін абсцисса өсіне
rор = (ri + ri+1) / 2
мәнін, ал ордината өсіне бөлшектерінің радиусы ri- мен rі+1 аралығында жатқан фракцияның F = Dpi /Dri шамасын салады. Мұндағы Dр = pi - рi+1; Dri = ri+1 - ri (3.8-сурет).
Дифференциалдық қисығы полидисперстік жүзгіндегі қай фракцияның массалық үлесі басым екендігін айқын көрсетеді. Мысалы, дифференциалдық қисығы а-қисығымен (3.8-сурет) өрнектелетін жүзгіндегі бөлшектерінің радиусы ri мен ri+1 аралығында жатқан фракцияның массалық үлесі басқа фракциялардікінен басым. Дифференциалдық қисығы дисперстік жүйенің маңызды сипаттамасы болып саналады. Дифференциалдық қисықтағы көрсетілген радиустар аралығы неғұрлым қысқа, ал максимумы биік болған сайын жүйе дисперстік құрамы жағынан монодисперстік жүйеге жақын келеді (а-қисығы). Керісінше, радиустар аралығы алшақ, ал максимумы оншалықты биік болмаса, онда жүйе дисперстік құрамы жағы-нан полидисперсті болғаны (б-қисығы). Интегралдық және дифференциалдық қисықтарын тұрғызуға қажетті тәжірибелік мәндерді төменде көрсетілген кесте түрінде жазған ыңғайлы.
3.3-кесте. Седиментацияның тәжірибелік мәндері
3.7 Коллоидтық бөлшектердің өлшемін анықтау әдістері Коллоидтық химия коллоидтық жүйелердің әртүрлі қасиеттерін зерттеу үшін белгілі физика-химиялық эксперименттік зерттеу әдістерімен қатар өзінің арнайы әдістерін қолданады. Солардың ішінде коллоидтық бөлшектердің өлшемін, яғни коллоидтық жүйелердің дисперстік дәрежесін анықтайтын әдістерге тоқталайық. Бұл жерде сол әдістердің бұрын айтылмағандарына толығырақ тоқталып, ал көпшіліктерімен бұрыннан таныс болғандықтан және алдағы тарауларда коллоидтық жүйелерде арнайы қасиеттерін қарастырғанда айтатын болғандықтан оларды қысқаша айтып өтеміз.
3.7.1 Ультрасүзгіштік (ультрафильтрациялық) әдіс Бұл тәсіл коллоидтық, иә ҮМҚ ертінділерін ерекше ультрасүзгіштер арқылы сүзуге негізделген. Бұл сүзгілердің ерекшелігі сол, олар еріткіштің, молекулаларын өткізіп жіберіп, коллоидтық бөлшектер мен ҮМҚ өткізбейді. Бұндай ультрасүзгілерді әртүрлі жолменен даярлайды. Осындай ультрасүзгі ретінде кәдімгі целофонды да қолдануға болады. Әрине ультрасүзгі әдісі бойынша коллоидтық бөлшектердің шамасын білу үшін сол сүзгілердің мөлшерінің орташа шамасы алдын ала белгілі болу керек.
3.7.2 Седиментациялық (шөгу) әдісі Бұл тәсілдің негізгі принциптерін седиментациялық талдауды өткенде қарастырдық. Ал олармен толығырақ лабораториялық сабақтардың нұсқаларымен танысуға болады. Айта кететін бір жағдай бұл әдіс коллоидтық бөлшектердің шамасын емес, ірі дисперстік жүйелердегі- жүзгіндердегі бөлшектердің шамасын анықтайды. Бұл тәсілді коллоидтық бөлшектердің шамасын анықтауға қолдану үшін жердің бөлшектерге әсер ететін тарту күшін одан оңдаған мың, иә жүздеген мың есе көп әсер ететін күшке ауыстыру керек. Бул ультрацентрифуга деп аталатын құралдың көмегімен жасалады. Енді соны қарастырайық.
3.7.3 Ультрацентрифугалық әдіс Ультрацентрифуганы коллоидтық бөлшектердің шамасын анықтауға қолдануды ең бірінші рет 1912 ж. А.В. Думанский айтқан болатын. А.В. Думанскийдің осы идеясын Швед ғалымы Сведберг кейінірек (1923 ж.) жүзеге асырып ультрацентрафуганың конструкциясын жасады. Ультрацентрифугалық әдіс, ультрацентрифуганың көмегімен коллоидтық ерітінді құйылған ерекше кюветадағы (ыдысшадағы) бөлшектердің центрифуганың айналу осьінен шетіне қарай ығысу (жылжу) жылдамдығын өлшеуге негізделген. Бұл жағдайда формуладағы g-дің орнына
жазуға болды. Мұнда Сонда Стокс теңдеуін былайша жазамыз:
Бұны интегралдап, r-ді тапсақ:
3.7.4 Диффузиялық әдіс Бұл әдіс диффузияметрлер деп аталатын ерекше аспаптарда кірнелердегі коллоидтық бөлшектердің диффузия жылдамдығын біле отырып, Эйнштейн теңдеуі бойынша бөлшектердің радиусын есептеп табуға болады. 3.7.5 Осмометрлік әдіс Бұл әдіс және осыған байланысты ертіндідегі заттың молекулалық салмағын табатын криоскопиялық әдіс коллоидтық бөлшектер мен ҮМҚ шамасын, дұрыс айтсақ орташа есеппен алынған шамасын табу үшін де қолдануға болады. Өйткені коллоидтық бөлшектер мен ҮМҚ шамалары мөлшері дисперстік фазаның сандық иә молекулалық салмағымен оның үстіне осмостық жене криоскоптық шамалар мен физикалық химиядан белгілі мына қатынас бойынша байланысты:
m – еріген заттың мөлшері; г – бойынша. Е3 – криоскопиялық константасы; b – еріткіштің мөлшері; М – сандық (мицеллярлық) салмақ.
Кірнелердегі сандық концентрацияның өте аз болуына, соның әсерінен осмос қысымы,
ТӨРТІНШІ ТАРАУ
4 КОЛЛОИДТЫҚ ЖҮЙЕЛЕРДІҢ ЭЛЕКТРЛІК ҚАСИЕТТЕРІ Коллоидтық жүйелерде, әсіресе дисперсиялық орта су болып келген жағдайдағы коллоидтық жүйелерде, дисперстік фаза бөлшектерінің беттерінде болатын зарядтардың маңызы зор. Сол себепті бұл тарауда дисперстік фаза қатты, ал дисперсиялық орта сұйық болып келетін коллоидтық жүйелердің электрлік қасиеттерімен танысамыз. Бұл тарауда бөлшек беттерінде зарядтардың пайда болу себептерін, қос электрлік қабаттың құрылысын және электр өрісінің әсерінен дисперстік бөлшектерде болатын құбылыстарды (электркинетикалық құбылыстары) және электркапиллярлық құбылыстарды қарастырамыз.
4.1. Электркинетикалық құбылыстар Дисперстік жүйелердегі бөлшектердің зарядтарының болуын алғаш рет Мәскеу университетінің профессоры Ф.Ф. Рейсс 1808 ж. ашқан болатын. Ол 4.1-суретте керсетілгендей ылғалды топыраққа (батпаққа) сумен толтырылған шыны түтікшелерді матырып, оларға электродтарға потенциал айырмасын туғызғанда болатын құбылыстарды байқады. Бұнда Ф.Ф. Рейсс электр өрісін туғызған кезде судың оң полюсті электрод тұрған жағы ылайланып, ал судың теріс полюсті электрод тұрған жері тұнық күйіндегі қалатынын байқады. Бұл тәжірибе топырақтың оң полюсті электродқа тасымалданатынын көрсетеді. Кейінгі зерттеулердің нәтижесінде бөлшектер электр өрісінің әсерімен бірқалыпты тұрақты жылдамдықпен тасымалданатыны дәлелденді. Көптеген тәжрибелердің нәтижесінде бөлшектердің жылдамдығы потенциалдар айырмасы және дисперсиялық орта тұрақтылығы артқан сайын өсетіндігі, ал ортаның тұтқырлығы өскен сайын оның кемитіндігі белгілі болды. Міне осыны - электр өрісінде дисперстік бөлшектердің тасымалдануын- электрофорез деп атайды (кейде оны катоферез деп те атайды). Егер U тәрізді түтікшелердің ортаңғы иінін жұқа кварц құмын салып толтырып, оған да электр өрісін туғызатын болсақ, онда түтікшенің теріс электрод тұрған бөлігіндегі су белгілі бір деңгейге көтерілетінін байқауға болады (4.2. сурет). Бул тәжірибені де алғаш рет Ф.Ф. Рейсс жасаған. Тәжірибедегі кварцтік құм уақ тесікті диафрагма рольін атқарады.
Электрфорез құбылысындағы сияқты, осы айтылған тәжрибедегі тасымалданған сұйық белгілі бір жылдамдықпен қозғалады екен және тасымалданған сұйықтың мөлшері потенциалдар айырмасы мен ортаның диэлектрлік өтімділігіне тура, ал ортаның тұрақтылығына, кері пропорционал екен. Бұл құбылысты, яғни электр өрісіндегі сұйықтықтың белгілі бір электродқа тасымалдануын,электросмос деп атайды (кейде оны электрэндоосмос деп те атайды). 1852 ж. Т.Видеман электросмос құбылысын сандық түрде зерттеді. Ол уақ тесікті диафрагмадан өтетін сұйықтық мөлшерінің тоқ күшіне байланыстылығын, ал тоқ күші тұрақты болғанда диафрагманың қалыңдығына байланыссыз екенін көрсетті. Сонымен Ф.Ф.Рейсс жоғарыда айтылған тәжрибелердің көмегімен бұрын белгісіз екі құбылысты (электросмос және электрфорез) ашты. Ф.Ф.Рейсс байқаған бұл құбылыстардың себептері бірдей екен, ол дисперстік жүйедегі сұйық (орта) және қатты (бөлшек) фазалардың әртүрлі зарядта болуынан екен. Электрфорез кезінде электр өрісінің әсерінен шамасы өте кішкентай болғандықтан дисперстік фазаның белшектері оң электродқа тасымалданады. Ал электросмос кезінде кварцтық құмның бөлшектері ірі болғандықтан электр өрісі нәтижесінде капиллярлар арқылы теріс электродқа оң зарядталған сұйықтық тасымалданады. Кейінірек келе электрфорез және электросмос құбылыстарына қарама - қарсы екі құбылыс байқалды. 1859 ж. Квинке уақ тесігі бар диафрагма арқылы сұйықтықты қысыммен өткізгенде, диафрагманың екі жағындағы электродтар арасында потенциалдар айырмасының болатынын байқады. Квинке пайда болған электрлік қозғаушы күштің (ЭҚК) диафрагманың қалыңдығы мен ауданына және өткен сұйықтықтың мөлшеріне байланыссыз, тек сұйықтықтың ағызатын қысымға байланыстылығын анықтады. Неғұрлым қысым көп болса, соғүрлым ЭҚК көп болады. Квинке ашқан электросмосқа қарама-қарсы болатын бүл құбылысты ағу потенциалы немесе Квинке эффектісі деп атайды. Квинкенің аспабының сұлбасы 4.3-суретте көрсетілген. Электрфорезге қарама-қарсы құбылысты 1878 ж. Дорн байқады. Ол дисперстік фазаның бөлшектері дисперсиялық ортада тұнғанда (шөккенде), мысалы құм суда шөккенде, сол шөккен бөлшектердің әртүрлі деңгейлерінде орналасқан электродтар арасында потенциалдар айырмасының болатынын көрсетті.
Бұл қүбылыс Дорн эффектісі немесе шөгу (тұну) потенциалы деп аталады. Міне осы құбылыстарды, - иә электр өрісінің әсерінен фазалардың қозғалысын, иә фазалардың қозғалысынан электр өрісінің туатынын байқауға болатындықтан электркинетикалық құбылыстар деп атайды. Сонымен электркинетикалық құбылыстарды 2 топқа бөлуге болады: 1. Бірінші текті электркинетикалық құбылыстар: оған электрофорез бен электросмос жатады. Бұлқұбылыстар кезінде электр өрісінің әсерінен фазалардың қозғалысын байқаймыз. 2. Екінші текті электркинетикалық құбылыстар: бұған седиментациалық потенциал (Дорн эффектісі) мен ағу потенциалы (Квинке эффектісі) жатады. Бұл құбылыстар кезінде амалсыз қозғалатын фазалардың нәтижесінде потенциалдар айырмасы пайда болатынын байқауға болады. 4.2. Электркапиллярлық құбылыстар Беттік керілу мен электрлік энергияның қарым-қатынасын Гиббстің адсорбциялық теңдеуі сияқты термодинамиканың І-және ІІ-заңдарының біріккен теңдеуінен алуға болады. Электрлік энергияның өзгерісін Химиялық энергияны еске алмаса, термодинамиканың I- және II- заңдарының біріккен түрі төмендегідей жазылады:
Бұл теңдеудегі
Гиббс энергияның толық дифференциалы мынаған тең:
Бұл теңдеуді (2.2)-теңдеуден алсақ:
Алынған өрнекті беттік қабаттың ауданына бөліп және
(2.3)-теңдеу Липпманның бірінші теңдеуі деп аталады. Егер потенциал мен зарядтың тығыздығының таңбасы бірдей болса, онда потенциалдың артуына байланысты беттік керілу төмендейді. Егер олардың таңбалары қарама–қарсы болса, онда потенциалдың артуы беттік керілудің өсуіне әкеп соғады. Бұл тәуелдіктің заряд тығыздығы абсолюттік мәні жоғары болған сайын күштірек болады. Егер жүйе тепе–теңдікке беттік энергияның өздігінен азаюының салдарынан ұмтылса, әдетте зарядпен ҚЭҚ-тың потенциалының таңбасы бірдей болады және беттік керілудің азаюы электрлік потенциалдың абсолюттік мәнінің азаюымен бірге жүреді. ҚЭҚ-тың дифференциалдық сыйымдылығы мына өрнекпен анықталады:
Мұны (2.4)-теңдеуге қойып, Липпманның екінші теңдеуін аламыз:
(2.5)-теңдеу, егер Егер ҚЭҚ және оған сәйкес фазааралық шекарада электрлік потенциал иондардың қайта таралуының салдарынан пайда болатын болса, онда иондардың адсорбциясын сипаттау үшін Гиббс теңдеуін пайдалануға болады. Егер бетте тек катиондар адсорбцияланатын болса, онда:
Мұндағы Г+ -потенциаланықтайтын катиондардың гиббстік
Зарядтың беттік тығыздығы мынаған тең:
|
|
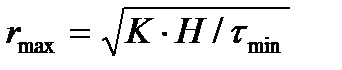 және
және  (6.12)
(6.12)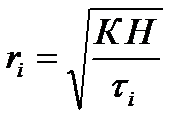 (6.13)
(6.13)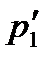 ,
, 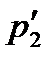 ,
, 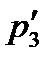 ,
, 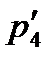 және
және  нүктелерін аламыз. Сондағы
нүктелерін аламыз. Сондағы 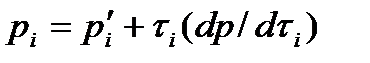 (6.14)
(6.14)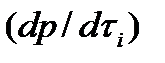 - берілген нүкте арқылы седиментация қисығына жүргізілген жанаманың абсцисса өсімен жасайтын бұрышының тангенсіне тең.
- берілген нүкте арқылы седиментация қисығына жүргізілген жанаманың абсцисса өсімен жасайтын бұрышының тангенсіне тең.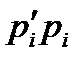 кесіндісіне тең болады. Сонда
кесіндісіне тең болады. Сонда 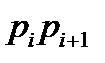 кесіндісі радиустары ri – ден кіші, бірақ ri+1-ден үлкен бөлшектерден тұратын фракцияның массалық пайыздық мөлшеріне сәйкес келеді.
кесіндісі радиустары ri – ден кіші, бірақ ri+1-ден үлкен бөлшектерден тұратын фракцияның массалық пайыздық мөлшеріне сәйкес келеді. шамасына тең. Сонда радиусы r1-ден үлкен бөлшектерден тұратын фракцияның жүзгіндегі пайыздық үлесі
шамасына тең. Сонда радиусы r1-ден үлкен бөлшектерден тұратын фракцияның жүзгіндегі пайыздық үлесі  шамасына, ал радиусы r5-ден үлкен бөлшектерден тұратын фракцияның жүзгіндегі пайыздық үлесі
шамасына, ал радиусы r5-ден үлкен бөлшектерден тұратын фракцияның жүзгіндегі пайыздық үлесі  шамасына тең болады. Осы мәндердің негізінде
шамасына тең болады. Осы мәндердің негізінде 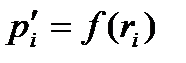 қисығын тұрғызады (3.7-сурет). Интегралдық қисығы жүзгіндегі фракциялардың пайыздық үлесін көрсетеді. Мысалы, радиусы r1 мен r2-нің аралығында жатқан бөлшектерден тұратын фракцияның жүзгіндегі пайыздық үлесі Dр12 = р‘2 - р'1 шамасына тең болады.
қисығын тұрғызады (3.7-сурет). Интегралдық қисығы жүзгіндегі фракциялардың пайыздық үлесін көрсетеді. Мысалы, радиусы r1 мен r2-нің аралығында жатқан бөлшектерден тұратын фракцияның жүзгіндегі пайыздық үлесі Dр12 = р‘2 - р'1 шамасына тең болады.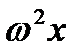
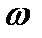 - бұрыштық жылдамдық; ал х- бөлшек айналу осьінен қашықтығы.
- бұрыштық жылдамдық; ал х- бөлшек айналу осьінен қашықтығы.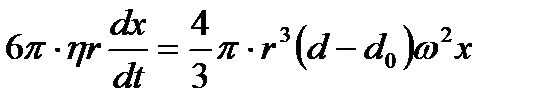
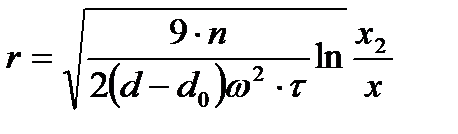
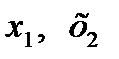 - белгілі бір уақыт аралығындағы бөлшектерді айналу осьінен қашықтығы. Оны фотоға түсіру арқылы золь мен таза дисперсиялық ортаның шекарасы арқылы анықтайды.
- белгілі бір уақыт аралығындағы бөлшектерді айналу осьінен қашықтығы. Оны фотоға түсіру арқылы золь мен таза дисперсиялық ортаның шекарасы арқылы анықтайды.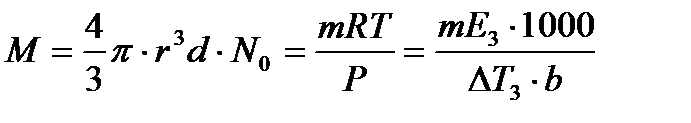
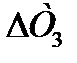 аз болуына байланысты және оларды анықтаудың қиындығына байланысты бұл әдіс онша дұрыс мағлұмат бермейді, Сондықтан да бұл тәсілді тек ҮМҚ ерітінділеріне қолдануға болады. Бұл жоғарыда айтылған әдістердің бәрі жалпы алғанда коллоидтық жүйелердің молекулалы-кинетикалық қасиеттеріне негізделген. Бұдан басқа да осы жүйелердің оптикалық қасиеттеріне негізделген ультрамикроскоптық, электрондық микроскоптық және құрылым талдау әдістерін де айта кеткен жөн. Олар туралы дисперстік жүйелердің оптикалық қасиеттерін қарастырғанда (өткен тарауда) айтқан болатынбыз.
аз болуына байланысты және оларды анықтаудың қиындығына байланысты бұл әдіс онша дұрыс мағлұмат бермейді, Сондықтан да бұл тәсілді тек ҮМҚ ерітінділеріне қолдануға болады. Бұл жоғарыда айтылған әдістердің бәрі жалпы алғанда коллоидтық жүйелердің молекулалы-кинетикалық қасиеттеріне негізделген. Бұдан басқа да осы жүйелердің оптикалық қасиеттеріне негізделген ультрамикроскоптық, электрондық микроскоптық және құрылым талдау әдістерін де айта кеткен жөн. Олар туралы дисперстік жүйелердің оптикалық қасиеттерін қарастырғанда (өткен тарауда) айтқан болатынбыз. (
(  - электрлік потенциал,
- электрлік потенциал, 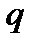 -беттік заряды)деп бегілейік.
-беттік заряды)деп бегілейік.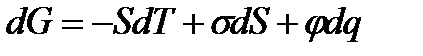 (2.1)
(2.1) беттік энергияның өзгерісін көрсетеді. Температура тұрақты болғанда (2.1)-теңдеу былайша жазылады:
беттік энергияның өзгерісін көрсетеді. Температура тұрақты болғанда (2.1)-теңдеу былайша жазылады: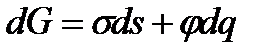 (2.2)
(2.2)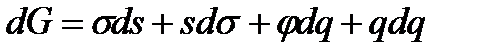
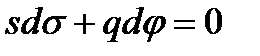
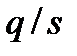 -ті
-ті  (
( 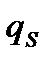 -бірлік беттің заряды, яғни зарятың тығыздығы)деп белгілеп, мынандай теңдеу аламыз:
-бірлік беттің заряды, яғни зарятың тығыздығы)деп белгілеп, мынандай теңдеу аламыз: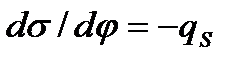 (2.3)
(2.3)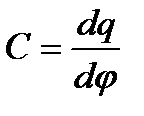 (2.4)
(2.4)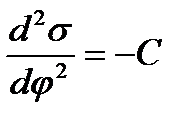 (2.5)
(2.5) мен
мен  тәуелділігі белгілі болса, ҚЭҚ сыйымдылығын анықтауға мүмкіндік береді.
тәуелділігі белгілі болса, ҚЭҚ сыйымдылығын анықтауға мүмкіндік береді.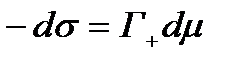 (2.6)
(2.6) адсорбциясы.
адсорбциясы. (2.7)
(2.7)