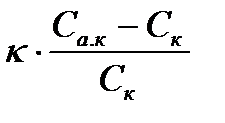|
|
Электролитпен коагуляциялау кинетикасы 18 глава
4.5.6 Дисперсиялық ортаның табиғатының әсері ҚЭҚ пайда болу себептерін қарастырғанда оның дисперсиялық ортаның полярлығына тәуелді болатынын білдік. Ендеше ортаның табиғаты ζ- потенциалына да әсерін тигізуі керек. Көптеген зерттеулер дисперстік фазаның ζ-потенциалы еріткіштің (ортаның) полярлығы көп болған сайын көп болатыны көрсетті. Келесі кестеде шыны капиллярларындағы әртүрлі сұйықтықтардың электросмостық тасымалдану жылдамдығы көрсетілген.
4.1- кесте. Әртүрлі сұйықтықтардың электросмостық тасымалдану жылдамдығы
Кестенің мәліметтері бойынша, сұйықтықтың полярлығы неғұрлым көп болса (ол диэлектрлік өтімділік пен дипольдік сәт арқылы сипатталады), соғұрлым электроосмостық тасымалдану жылдамдығы көп болатынын байқаймыз.
4.6 Лиофобтық коллоидтық мицелланың құрылысы Қос электрлік қабаттың құрылысының теориясы дисперстік фазаның бөлшегінің құрылысын түсіндіруге мүмкіндік береді. XX – ғасырдың алғашқы ширегінде коллоидтық жүйенің құрылысын түсіңдіру үшін мицеллалық теория жасалды. Ол теория әрі лиофобтық, әрі лиофильдік кірнелердің құрылысын түсіндірді. Бірақ кейін келе, лиофильдік кірненің, яғни ҮМҚ ертіңділерінің құрылысы лиофобтық кірненің құрылысынан өзгеше, кәдімгі молекулалық ертінділердің құрылысына жақын екені дәлелдеңді. Сол себепті мицеллалық теория осы кезде тек лиофобтық кірненің құрылысын ғана түсіндіреді. Бұл теория жасауда орыс ғалымдары - П.П. Веймарн, А.В. Думанский, Н.П. Песков, С.М. Липатов т,б. ғалымдардың жұмыстарының маңызы зор. Бұл теория бойынша, кез-келген лиофобтық кірнелер 2 бөліктен тұрады: мицелладан және интермицеллалық (мицелла аралық) сұйықтықтан. Мицелла – дисперстік бөлшектердің бірігіп, дисперстік фаза беретін бөлігі. Ал интермицеллалық сұйықтық - мицеллаға кірмейтін сол кірненің дисперсиялық орта және оған қоса онда болатын электролит пен электролит еместерден тұратын бөлігі. Енді сол мицелланың өзінің құрылысына тоқталайық. Сурет
AgJ кірнесін мысалға алып, оның құрылысын түсіндірейік. Ол кірнеміз KJ ертіндісінде болсын. Панет-Фаянс ережесін еске ала отырып, мицелланың құрылысын 4.19 - суретте көрсетілгендей етіп сұлбамен көрсетуге болады. Мицелланың ортасында AgJ - тың бірнеше молекуладан тұратын кристалл болады. Н.П. Песковтың ұсынысы бойынша оны агрегат деп атайды. Агрегаттарға потенциал анықтағыш иондардың адсорбциясының нәтижесінде ол агрегатқа электрлік заряд тудырады. Міне осы потенциал анықтағыш иондардың адсорбцияланған бөлігін агрегатпен біріктіріп айтқанда мицелланың ядросы деп атайды. Ядро маңайында өте аз қашықтарда олармен қарсы иондардың К + біразырақ бөлігі өте тығыз байланыста болады. Электр өрісінің нәтижесінде қарсы иондардың осы айтылған бөлігін ядромен бірге анодқа қозғалады. Ядроны онымен мықты байланыста болатын қарсы иондармен біріктіріп коллоидтық бөлшек деп атайды. Мицелладан коллоидтық бөлшектің айырмашылығы, мицелла электрбейтарапты болса, коллоидтық бөлшек әрқашан зарядты болады. Мысалы қарастырып отырған жағдай үшін, теріс зарядты болады. Ал қарсы иондардың қалған бөлігі мицелланың диффузиялық қабатын түзеді. Электр өрісінің нәтижесінде, мысалы, электрфорез құбылысында, мицелла коллоидтық бөлшек пен диффузиялық қабаттың аралығында екіге «жарылады», оны жылжу (сырғу) жазықтығы, иә жылжу шекарасы деп атайды. Мицелланың құрылысын жазуға ыңғайлы формула жүзінде де көрсетуге болады. Мысалы, AgJ кірнесінің мицеллааралық сұйық KJ болған кездегі құрылысының формуласын былайша көрсетуге болады:
Мұнда әрқашанда
Егер AgJ кірнесі AgNO3 ертіндісінде болса, онда оның мицелласының құрылысын былайша жазуға болады.
Дәл осы сияқты кремний қос тотығының гидрокірнесінің (1) темір гидраттарының гидрокірнесінің (2) мицеллаларының құрылыстарын жазуға болады:
Потенциаланықтағыш ион бір валентті болып келгенде, коллоидтық бөлшектің оң, иә теріс зарядталғанына байланысты мицелланың құрылысының жалпы формуласын төмендегіше көрсетуге болады.
Мұндағы A- – аниондар; К+ – катиондар; Ал квадраттық жақшада агрегат, и фигуралық жақшада коллоидтық бөлшек. Кейбір ескі оқулықтарда коллоидтық бөлшекті зарядталған кешен, иә гранула(түйіршік) деп те атайды. 4.7 Электрфорез және электросмос құбылыстарын сандық түрде сипаттау. Гельмгольц-Смолуховский теңдеуі Біз осыған дейін электркинетикалық құбылыстарды жалпы түрде сапалық жағынан қарастырдық. Енді практикада көп қолданылатын электрфорездік жылдамдық пен электросмостық тасымалдау жылдамдығын анықтаудың элементарлық теориясына тоқталайық. Өйткені бұл айтылған шамалар арқылы коллоидтық жүйені сипаттайтын ξ-потенциалын есептеуге болады. Алғаш Квинке электркинетикалық құбылыстарды фазааралық қос электрлік қабаттың болуымен түсіндірді. Одан кейін Гельмгольц оның теориясын ары дамытып электркинетикалық құбылыстарды сандық түрде түсіндірді. Гельмгольц электркинетикалық құбылыстарды түсіндіргенде мынандай жағдайды еске алды: 1. Қатты дене мен сұйықтық беттерінің зарядтары қарама-қарсы және бір-біріне параллель орналысып қос электрлік қабат түзеді. 2. Қос электрлік қабаттың қалыңдығы молекулалық шамаға шамалас. 3. Электркинетикалық құбылыстар кезінде қатты фаза бетінде болатын сұйықтық жылжымайды да, ал қалған сұйықтық жылжиды және оған кәдімгі сұйықтыққа қолданылатын үйкелу заңын қолдануға болады. 4. Электркинетикалық құбылыстар кезінде сұйықтықтардың ағуы ламинарлық түрде болады және оны кәдімгі гидродинамикалық теңдеулермен сипаттауға болады. 5. ҚЭҚ - жазық параллельді конденсатор сияқты қарастыруға болады. 6. Зарядтардың қос электрлік қабатта орналасуы сыртқы электр өрісіне байланыссыз болады. 7. Қатты фаза - диэлектрик, ал сұйық фаза тоқ өткізетін фаза болады. Осы айтылғандарды еске ала отырып электросмос пен электрфорездің жылдамдығы мен ξ-потенциалының арасындағы байланысты табуға болады. Қатты денемен байланысқан потенциаланықтағыш иондармен ерітіндідегі қарсы иондардың қашықтығы δ болсын. Қатты дененің бірлік беттеріндегі заряд q-ға тең болсын. Бұл шаманы басқаша электрдің беттік тығыздығы деп қарастыруға болады. Жүйе электрбейтарапты болғандықтан сұйықтықтағы зарядтардың беттік тығыздығы да q-ға тең болады, әрине оның таңбасы қарама-қарсы болады. Қашықтығы өте аз болғандықтан фазааралықтың қисықтылығын еске алмай қос электр қабатты жазық конденсатор деп қарастыруға болады. Жазық конденсатор үшін δ, q және ξ шамаларының арасындағы қатынасты былайша қарастыруға болады:
ε - конденсатор арасындағы заттың абсолюттік диэлектрлік өтімділігі.
Бұл теңдеуді басқаша былайша жазуға болады:
Егер қос электр қабатқа потенциал айырмасы E тангенстік түрде әсер етсе 4.19 - суретте, электродтардың қашықтығы
Сурет.
Тангенстік фазааралық беттегі екі фазаны бір-біріне салыстырмалы түрде қозғайтын электрлік күш потенциалдар айырмасының градиенті Н болғанда мынаған тең:
Стационарлық режимде электрфорез немесе электросмос құбылыстарының жылдамдықтары тұрақты болады, өйткені қозғалтатын электрлік күш пен үйкелу күші теңеседі. Ньютон заңы бойынша бірлік бетке сәйкес келетін үйкелу күші мынаған тең:
Мұндағы η- сұйықтықтың динамикалық тұтқырлығы; u –сұйықтың қатты фазаға қарағандағы қозғалу жылдамдығы; х – сұйықтың жылдамдығы өзгеретін аралықтағы қалыңдығы, қарастырып отырған жағдай үшін оны δ-ға тең деп алуға болады. Қос электрлік қабатта сұйықтықтың ағу жылдамдығы қашықтыққа тура пропорцианал өзгереді деп, және δ=x деп есептейік: Электрфорез, иә электросмос құбылысы кезінде олардың жылдамдықтары тұрақты, өйткені (F1) және үйкелу (F2) күштері өзара тең: F1=F2 ендеше:
q-ның жоғарғы теңдеудегі мәнін осыған қойып, U – ды табатын болсақ, Гельмгольц-Смолуховский теңдеуін алуға болады:
Көптеген жағдайда электрфорездің тасымалдану жылдамдығын потенциалдық градиенттің бірлігіне есептейді.
U0-ді электрфорездік жылдамдық, (шапшандылық) деп атайды. Оны коллоидтық жүйелердің электрфорезге қабілеттілігін салыстыру үшін қолданады. Гельмгольц-Смолуховский теңдеуін ξ- потенциалы бойынша шешсек, былайша жазуға болады:
Бұл формуладағы электрфорез, иә электросмос жылдамдығын біле отырып ξ-потенциалын есептеуге болады. Формуладағы қалған шамалар қарастырып отырған жүйе үшін тұрақты шамалар. Егер сырттан берілетін потенциалдар айырымын E вольт, ал
Бұдан абсолюттік электростатикалық бірлік бойынша ξ-потенциалын былайша табуға болады:
Ал практикада басқа потенциалдар сияқты ξ-потенциалын вольт арқылы белгілейтіндіктен, оны в бойынша есептеу үшін соңғы теңдеудің оң жағын тағы да 300-ге көбейту керек:
Көптеген кірнелердің эксперимент арқылы анықталған электркинетикалық ξ-потенциалының мәні әдетте 20 мен 90 мв аралығында болады. Электрофорезге эксперимент жүргізгенде құрылысы практикумдерде жазылған арнайы U – тәрізді түтікшеге түсті кірне (золь) (Fe(OH)3, MnO2 немесе т.б.) құйып, оны тұрақты ток көзіне қосып, түсірілген кернеудің градиентін (Н) табады:
Мұндағы Е – кернеу, вольт бойынша;
Электрофорездік жылдамдықты табу үшін белгілі-бір уақыт аралығындағы (әдетте 3 мин.) кірненің жүрген жолын тауып, оны мына формулаға қойып есептейді:
Мұндағы Электркинетикалық потенциал мына формуламен есептелінеді:
Мұндағы Бұл соңғы қарастырылған жағдайда ξ-потенциалының мәні бірден вольт бойынша шығады, өйткені формулаға барлық шамалардың өлшем бірліктері ӨЖ(СИ) жүйесі бойынша алынады. Гельмгольц-Смолуховский теңдеуін пайдаланып электркинетикалық потенциалды электросмос құбылысы бойынша да анықтауға болады:
ζ
Мұндағы: ϑ - дисперсилық ортаның көлемдік жылдамдығы (ϑ=U0 /S, S-кеуек денедегі барлық капиллярдың қима бетінің ауданы.); I-ток күші; æ-меншікті электр өткізгіштік; Ендеше соңғы формула бойынша тәжірибе жүзінде анықталған ϑ, æ, ƞ және I мәндері бойынша ζ- потенциалын есептеуге болады екен. Екінші текті электркинетикалық құбылыстар бойынша да ζ- потенциалын анықтауға болады. Мысалы, ағу потенциалында (эффектісінде)электркинетикалық потенциал мен ағу потенциалы (Uағу) арасындағы байланысты Гельмгольц-Смолуховский теңдеуі арқылы былай жазуға болады: ζ Мұндағы: ∆p-жартылай өткізгіш жарғақтың екі жағындағы қысымдар айырмасы. Шөгу потенциалы (седиментациалық потенциал немесе Дорн эффектісі) жағдайында да электркинетикалық потенциалды Гельмгольц-Смолуховский теңдеуімен есептейді. Ол кезде электркинетикалық потенциалды былай өрнектейді: ζ
Мұндағы: ɳ- дисперсиялық ортаның тұтқырлығы; дисперсиалық ортаның меншікті электрөткізгіштігі; r- дисперсті фаза бөлшектерінің радиусы;
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР 1. Қоқанбаев Ә. Коллоидтық жүйелердің қасиеттері. Оқу құралы, Алматы «Қазақ университеті» 2002., 71 б. 2. Мұсабеков Қ.Б., Әбдиев Қ.Ж.. Коллоидтық химияның негіздері. Оқу құралы, Алматы «Қазақ университеті» 2008., 178 б. 3. Фридрихсберг Д.А. Курс коллоидной химии. Санкт-Петер-бург: Химия, 1995. -368 с. 4. Фролов Ю.Г. Курс коллоидной химии. Поверхностные явления и дисперсные системы. Москва: Химия, 1989. -464 с. 5. Щукин Е.Д., Перцов А.В., Амелина Е.А. Коллоидная химия. Москва: Высшая школа, 2006. -444 с. 6. Гельфман М.И., Ковалевич О.В., Юстратов В.П. Коллоидная химия. Санкт-Петербург. Москва. Краснодар: Лань, 2008. -336 с. 7. Воюцкий С.С. Курс коллоидной химии. М.: Химия, 1975. 8. Практикум и задачник по коллоидной химии. /Под ред. В.В. Назарова, А.С. Гродского. –М: ИКЦ «Академкнига», 2007. -374 с. 9. Адамсон А. Физическая химия поверхностей. Перевод с английского. /Под ред. З.М. Зорина и В.М.Муллера. Москва: Мир, 1979. -568 с. 10. Қоқанбаев Ә.Қ. Коллоидтық химия терминдерінің орысша-қазақша және қазақша-орысша сөздіктері. Алматы: Баспагер, 1993. 11. Қоқанбаев Ә.Қ., Мұсабеков Қ.Б., Ерболат Ш. Коллоидтық химияның демонстрациялық тәжірибелері. Алматы «Қазақ университеті», 2002 ж. 151 б. 12. Қоқанбаев Ә.Қ., Мұсабеков Қ.Б., Түсіпбаев Н.Қ., Мұқаева Ж.З. Коллоидтық химияның есептері мен жаттығулары. Алматы, «Қазақ университеті» 2006 ж.128 б.
Ә.Қ. Қоқанбаев КОЛЛОИДТЫҚ ЖҮЙЕЛЕРДІҢ ТҰРАҚТЫЛЫҒЫ ЖӘНЕ ҚҰРЫЛЫМ ТҮЗУІ Алматы 2007 Бірінші тарау. КОЛЛОИДТЫҚ ЖҮЙЕЛЕРДІ АЛУ ЖӘНЕ ТАЗАРТУ ӘДІСТЕРІ 1.1 Коллоидтық жүйелерді алу әдістері Коллоидтық жүйелердегі дисперстік фазаның бөлшектерінің шамалары шын ерітінділер мен суспензияның бөлшектерінің өлшемдерінің аралығында болады. Ендеше оларды еріген заттың молекулаларын, иондарын агрегатқа біріктіріп немесе ірі бөлшектерді ұнтақтау арқылы алуға болады. Осыған сәйкес Сведберг коллоидтық жүйелерді алу әдістерін екіге бөлді: конденсациялық және диспергациялық әдістер деп. Бұлардан өзгеше тағы өздігінен диспергілену жәнепептизация әдістері бар. Бұл соңғы әдіс тұнбаны коллоидтық ерітіндіге айналдыру әдісі. Онда алғашқы тұнбаның өзінде бөлшектердің коллоидтық размерлері болады. Айта кететін бір жағдай коллоидтық жүйелерді алу үшін және оны тұрақты ету үшін мынандай жағдайлардың болуы шарт: 1. Коллоидтық жүйелер гетерогендік болғандықтан, дисперсиялық ортамыз дисперстік фазаны өзіне өте жақсы ерітпеуі керек. Мысалы: NaCl-эфирде, күкірт – суда т.б. Олай болмаған жағдайда дисперстік фаза бөлшектері еріткіште жақсы еріп кетіп, гомогендік жүйе береді. 2. Ұнтақталған (ұсақталған, дисперленген) фаза бөлшектерінің шамасы коллоидтық бөлшектердің дисперстілігінің шамасындай болу керек ( Д=10-5 – 10-7 см). 3. Жүйенің өздігінен дисперстілігін азайтатын қасиетін жою үшін оған стабилизатор деп аталатын қоспа (көбінде ондай қоспаның ролін электролит атқарады) қосу керек. Ол коллоидтық бөлшектерді бірдей зарядтап, олардың тұрақтылығын арттырады. Міне осы жағдайларды еске ала отырып коллоидтық жүйелерді жоғарыда айтылған екі әдістердің біреуімен алуға болады екен. Осы екі әдістердің негіздерін схема түрінде былайша көрсетуге болады:
Бұдан осы екі әдістердің бір-біріне қарама-қарсы екенін көруге болады. Егер конденсациялық тәсіл кезінде жүйенің потенциалдық (химиялық т.б.) энергиясы кемісе, ал диспергациялық тәсіл кезінде бөлшектердің меншікті беті көбейеді, ендеше оған сәйкес жүйенің еркін беттік энергиясыда көбейеді. Бұл әдіс кезінде жүйеге сырттан энергия жұмсалуы керек. Кеңес одағы кезінде бүкіл елде 1 жылда өндіретін цементті ұнтақтау үшін Волга су электр станциясынан 1 жылда беретін энергиясындай энергия жұмсау керек болған екен. Міне бұдан 2 әдістің біріншісі, яғни конденсациялық әдіс энергетикалық жағынан қолайлы екені көрініп тұр. Енді осы әдістерді жеке-жеке қарастырайық. 1.1.1 Конденсациялық әдістер Конденсациялық әдістер арқылы коллоидтық жүйені алуды әдетте кристаллизация процесі сияқты қарастырады. Ал бұл әдіспен алынған бөлшектер өте кіші кристалл бөлшектер ретінде қарастырылады. Мұндай көзқараста орыс ғалымы Л.Л. Веймарн да болған. Ол - осы конденсациялық әдісті алғаш зерттеген ғалымдардың бірі. Кәдімгі кристалдардың түзілуі екі сатыда жүреді: 1. Бастапқы туынтектің (кристаллизация орталығының) пайда болуы. 2. Бастапқы туынтектердің өсуі. Бұдан біршама ірі кристалдар түзіледі. Көп уақытқа дейін кристалдардың бастапқы туынтегінің пайда болуын өз бетінше жүреді деп есептеді. Мұндай көзқарасты Тамман дамытты. Оның ойынша аса қаныққан ерітінді метастабильдік жағдайда болғанда, еріген молекулалар, иә иондар өз беттерінше бастапқы туынтек беріп, ол одан әрі өседі деп қарастырды. Бұл көзқарас бойынша бастапқы туынтектің пайда болу жылдамдығы U1, аса қанығуға тура пропорционал, оны былайша көрсетуге болады:
U1=
K – пропорционалдық коэффицент, Cа.қ. – аса қаныққан ерітіндінің концентрациясы. Cқ. – қаныққан ерітіндінің концентрациясы (басқаша, ол заттың ерігіштігі).
Теңдеуден неғұрлым Cа.қ.– Cқ. айырымы көп болса, неғұрлым Cқ. аз болса соғұрлым бастапқы туынтек жылдам пайда болатыны көрініп тұр. Кейінгі зерттеулер бастапқы туынтектің пайда болуы молекулалар, иә иондардың концентрациясының флуктуациясының нәтижесінде өзара соқтығысуынан емес, сол жүйеде кездейсоқ болатын басқа текті шаң-тозаңдарға ілескен заттың шөгуінен болатынын дәлелдеді. Мысалы: егер ерітінді басқа текті қоспадан тазартылған болса, яғни өте таза жүйеде аса қаныққан жағдайда да кристалшалардың пайда болмайтыны, ал ондай ерітінділерге басқа текті бастапқы туындылар, иә еріген заттың кристаллизацияларын енгізсек кристаллизация құбылысы өте тез жүреді екен. |
|
 , дипольдік сәт,
1018 э.с.б.
, дипольдік сәт,
1018 э.с.б.
 *105 см3/с*в
*105 см3/с*в
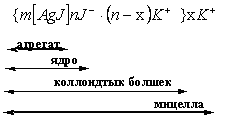
 болады. Бұл формуладағы m - AgJ - агрегатты құрайтын AgJ - молекуласының саны; n – потенциал анықтағыш иондардың саны; (n-x) – ядро жақын орналасқан қарсы иондардың саны; х – диффузиялық қабаттағы қарсы иондардың саны.
болады. Бұл формуладағы m - AgJ - агрегатты құрайтын AgJ - молекуласының саны; n – потенциал анықтағыш иондардың саны; (n-x) – ядро жақын орналасқан қарсы иондардың саны; х – диффузиялық қабаттағы қарсы иондардың саны.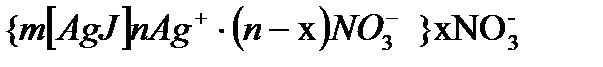
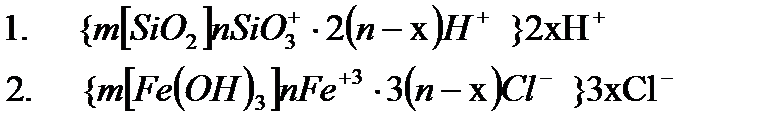
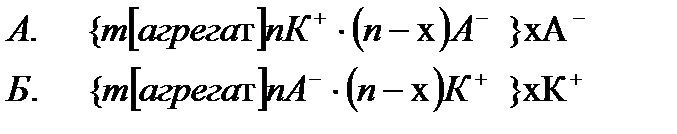
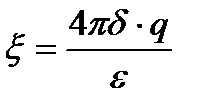
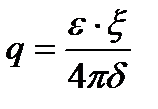
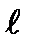 болса, сыртқы өрістің потенциалдар айырмасының градиенті (Н) мынаған тең:
болса, сыртқы өрістің потенциалдар айырмасының градиенті (Н) мынаған тең: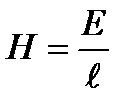
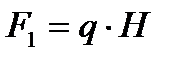
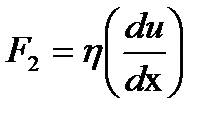
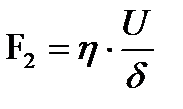

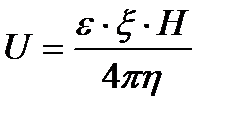
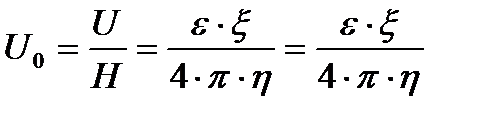
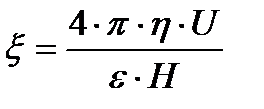
 -ді см арқылы өлшесек, онда:
-ді см арқылы өлшесек, онда: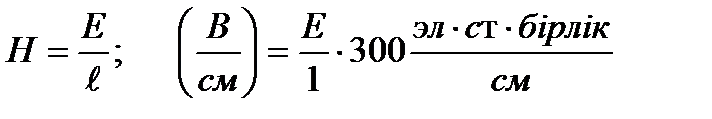
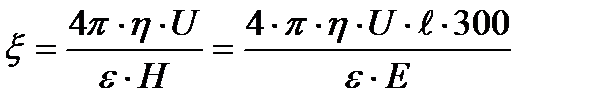
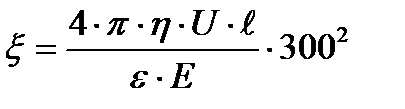
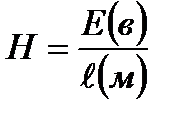
 - екі электродтың ара-қашықтығы, м бойынша.
- екі электродтың ара-қашықтығы, м бойынша.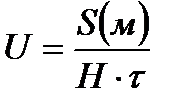
 - уақыт, секунд бойынша.
- уақыт, секунд бойынша.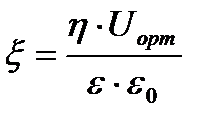
 (Д) – судың диэлектрлік тұрақтылығы;
(Д) – судың диэлектрлік тұрақтылығы; 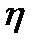 - судың тұтқырлығы
- судың тұтқырлығы  ;
;  - 8,85·10-12 д/м
- 8,85·10-12 д/м
 æ ⁄ (ε
æ ⁄ (ε  ∆p)
∆p) ⁄
⁄ 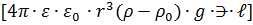
 және
және  0 –дисперстік фаза мен дисперсиялық ортаның тығыздықтары; ⋺- дисперстік фаза бөлшектерінің сандық концентрациясы; ℓ-екі электродтың ара қашықтығы;
0 –дисперстік фаза мен дисперсиялық ортаның тығыздықтары; ⋺- дисперстік фаза бөлшектерінің сандық концентрациясы; ℓ-екі электродтың ара қашықтығы;