|
|
Если (1) и (2) подставить в (7) то тогда получим
Уравнения (7) и (8) выражают закон изменения импульса частицы: уравнение (7) относительно неподвижной системы отсчета, а уравнение (8) относительно подвижной системы отсчета. Проецируем (7) и (8) на оси O¢X¢ и O¢Y¢ mVK cosaK + mV0 cosa0=FDt , (9) mVK sinaK = mV0 sin a0 , (10) mVK¢ cosaK¢ + mV0¢ cosa0¢=FDt , (11) mVK¢ sinaK¢ = mV0¢ sin a0¢.(12) Так как удар частицы о стенку абсолютно упругий, то будет выполняться закон сохранения механической энергии
Отсюда находим V0¢= VK¢ . (13) Подставляя (13) в (12) получаем sin a0¢= sin aK¢, или a0¢=aK¢(14) Определим угол a0¢. С этой целью преобразуем (3) и (4). Первоначально из (3) находим V0¢ cosa0¢=U+V0 cosa0,(15) А затем делим (4) на (15), в итоге находим
следовательно, согласно (14) aK ¢=46°6¢ Далее из формулы (4) определяем
Переходим к расчету конечных характеристик. Разделив (6) на (5), получаем
aK=36°35¢ (19) Тогда из (6) находим
Проверка! Из (10) имеем
Модуль изменения импульса частицы согласно (8) и (11) будет равен
Или в соответствии с (13) и (14) получаем
Подставляя численные значения (17) и (18) находим
Проверка! Согласно (7) и (9) имеем
Подставляя численные значения, в частности (19) и (20), получаем
Модуль средней силы будет равен
Задача 1.3 Нерелятивистская частица с внутренней энергией E0 и массой m0, летящая со скоростью На рис. 4 φ — угол разлета частиц, т.е. угол, образованный векторами
Таблица №3
Таблица №3 (продолжение) Основные зависимости в задаче 1.3 При распаде частицы выполняются законы сохранения импульса и энергии. Соответствующие уравнения в общем случае для данной задачи имеют вид
Задача 2.2 Однородный тонкий вертикальный стержень длины l=1м, движущийся поступательно в плоскости рисунка с горизонтальной скоростью Варианты столкновения: а) Центр тяжести стержня выше горизонтальной поверхности преграды (рис. 6) б) Центр тяжести стержня ниже горизонтальной поверхности преграды (рис.7)
Другие обозначения: wK - угловая скорость стержня в момент его удара о горизонтальную поверхность преграды; w0 - угловая скорость стержня сразу после удара о ребро преграды. Для варианта б):
jm - максимальный угол поворота стержня после удара. Начинать расчет для варианта столкновения б) следует с определения характерной скорости Другие исходные данные и искомые величины для каждого варианта задания представлены в таблице № 5. Таблица №5
Задача 3.1
Колебательная система (КС), представленная на рис. 10, 11, 12, 13, состоит из шайбы массой m и двух упругих пружин, имеющих жесткости k1 и k2 . На рис. 10, 12 шайба колеблется под действием пружин, соединенных параллельно, а на рис. 11, 13 колебания происходят под действием пружин, соединенных последовательно. Массой пружин можно пренебречь. На рис. 10, 11 КС имеет горизонтальное расположение, а на рис. 12, 13 вертикальное расположение в поле силы тяжести. l10 и l20 – длины 1-ой и 2-ой пружин в недеформированных состояниях; L (на рис.10, 12)—длина каждой пружины в деформированном состоянии; L (на рис.11, 13) — общая длина двух пружин в деформированном состоянии; Таблица №8 (к рис. 10)
Таблица №9 (к рис. 11)
Таблица №10 (к рис. 12)
Таблица №11 (к рис. 13)
1000 000 000 000 000 000 = 1018 экса Э квинтиллион 1000 000 000 000 000 = 1015 пета П квадриллион 1000 000 000 000 = 1012 тера Т триллион 1000 000 000 = 109 гига Г миллиард 1000 000 = 106 мега М миллион 1000 = 103 кило к тысяча 100 = 102 гекто г сто 10 = 101 дека да десять 0,1 = 10-1 деци д одна десятая 0,01 = 10-2 санти с одна сотая 0,001 = 10-3 милли м одна тысячная 0,000 001 = 10-6 микро мк одна миллионная 0,000 000 001 = 10-9 нано н одна миллиардная 0,000 000 000 001 = 10-12 пико п одна триллионная 0,000 000 000 000 001 = 10-15 фемто ф одна квадриллионная 0,000 000 000 000 000 001 = 10-18 атто а одна квинтиллионная Латинский алфавит
Греческий алфавит
Содержание. 1. Кинематика поступательного и вращательного движений. 5 2. Динамика поступательного движения материальной точки. 11 3. Динамика вращательного движения. 16 4. Работа. Мощность. Энергия. 23 5. Давление жидкости. Поверхностные явления. Внутреннее трение в жидкости. 27 6. Механические колебания. Гармонические колебания. Затухающие колебания. Волны в упругой среде. Акустика. 32 7. Молекулярная физика. 42 8. Физические основы термодинамики. 49 9. Энтропия. 55 10. Реальные газы. 57 Качественные задачи ………………………………………………... 61 Расчетно-графическая работа ………………………………………..84
|
|
. (8)
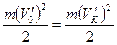
(16)
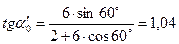, отсюда a0¢=46°6¢ , (17)
(18)
; 
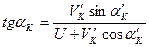
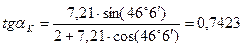
. (20)
; 
.
.
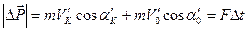
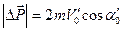
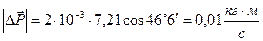
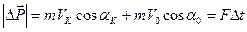
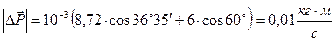
, распадается на две нерелятивистские частицы, скорости которых 
и 
, массы m1 и m2, импульсы 
и 
, кинетические энергии E1 и E2. При этом часть внутренней энергии E0 исходной частицы в количестве η E0, где коэффициент η<1 , расходуется на увеличение кинетической энергии образовавшихся частиц.
и 
.
Общие исходные данные: m* = 10-2 кг, V* = 10 м/с, φ * = π/2, E* = 10 Дж , η*=0,5. Другие исходные данные и искомые величины для каждого варианта задания представлены в таблице №3.
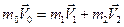
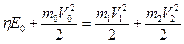
- минимальная горизонтальная скорость стержня, при которой он способен коснуться горизонтальной поверхности преграды;
\
– возможные векторы начальной скорости шайбы. Шайбу, находящуюся в положении равновесия, смещают до расстояния L, а затем импульсом придают ей в начальный момент времени t = 0, в соответствии с заданием, скорость 
(см. таблицы № 8 - 11). В результате КС приходит в колебательное движение.