|
|
Давление жидкости. Поверхностные явления.Внутреннее трение в жидкости. 1. Расход жидкости в трубке тока: а) объемный расход:
б) массовый расход:
где S – площадь поперечного сечения трубки тока; v – скорость жидкости; ρ – плотность жидкости. 2. Уравнение неразрывности струи:
где S1 и S2 – площади поперечного сечения трубки тока в двух местах; v1 и v2 – соответствующие скорости течений. 3. Уравнение Бернулли:
4. Скорость течения жидкости из малого отверстия в открытом широком сосуде:
где h – уровень жидкости относительно отверстия. 5. Поверхностное натяжение:
где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости. 6. Формула Лапласа, выражающая давление Р, создаваемое сферической поверхностью жидкости:
где R – радиус сферической поверхности. 7. Высота подъема жидкости в капиллярной трубке определяется по формуле Жюрена:
где Θ – краевой угол; ρ – плотность жидкости; r – радиус капилляра. 8. Высота подъема жидкости между двумя близкими и параллельными плоскостями:
где d – расстояние между плоскостями. 9. Объем жидкости (газа), протекающей за время t через длинную трубку:
где r – радиус трубки ; l – длина трубки; Δр – разность давлений на концах трубки, η – коэффициент внутреннего сопротивления. 10. Число Рейнольдса для потока жидкости в длинных трубках
где (v) – средняя по сечению скорость течения жидкости; 11. Число Рейнольдса для движения шарика в жидкости:
где v – скорость шарика; d – диаметр шарика. 12. Сила сопротивления F, действующая со стороны потока жидкости на медленно движущийся в ней шарик (формула Стокса):
где r – радиус шарика; v – скорость шарика. Задачи. 1. Найти скорость течения по трубе углекислого газа, если известно, что за полчаса через поперечное сечение трубы протекает 0,51 кг газа. Плотность газа принять равной 7,5 кг/м3. Диаметр трубы равен 2 см. 2. В дне цилиндрического сосуда имеется круглое отверстие диаметром d=1 см. Диаметр сосуда D=0,5 м. Найти зависимость скорости v понижения уровня воды в сосуде от высоты h этого уровня. Найти численное значение этой скорости для высоты h=0,2 м. Молоко течёт по молокопроводу диаметром 38 мм (установка УДС-1). На одном участке диаметр трубы уменьшился до 30 мм. На сколько изменится давление молока в этом участке трубы по сравнению с остальной частью трубы? Скорость течения молока в основной части трубы 2м/с. 4. Как высотой h=1,5 м наполнен до краёв водой. На расстоянии d=1 м от верхнего края бака образовалось отверстие малого диаметра. На каком расстоянии l от бака падает на пол струя, вытекающая из отверстия. 5. Струя воды с площадью S1 поперечного сечения, равной 4 см2, вытекает в горизонтальном направлении из брансбойда, расположенного на высоте Н=2 м над поверхностью Земли, и падает на эту поверхность на расстоянии l=8 м. Пренебрегая сопротивлением воздуха движению воды, найти избыточное давление Р воды в рукаве, если площадь S2 поперечною сечения рукава равна 50 см2. 6. Трубка имеет диаметр d=0,2 см. На нижнем конце трубки повисла капля воды, имеющая в момент отрыва вид шарика. Найти диаметр d2 этой капли. 7. Масса m 100 капель спирта, вытекающего из капилляра, равна 0,71 г. Определить поверхностное натяжение α спирта, если диаметр d шейки капли в момент отрыва равен 1 мм. 8. В воду опущена на очень малую глубину стеклянная трубка с диаметром d внутреннего канала, равным 1 мм. Найти массу воды m, вошедшей в трубку. 9. Капиллярная трубка диаметром d=0,5 мм наполнена водой. На нижнем конце трубки вода нависла в виде капли. Эту каплю можно принять за часть сферы радиуса r=3 мм. Найти высоту h столбика воды в трубке. 10. Какую работу А надо совершить при выдувании пузыря, чтобы увеличить его объем от V1=8 см3 до V2= 16 см3? Считать процесс изотермическим. (α=4 · 10-2 Н/м). 11. Какая энергия выделится при слиянии двух капель ртути диаметром d1=0,8 мм и d2=1,2 мм в одну каплю. (α=0,5 Н/м, ρ=13,6 · 103 кг/м3) 12. Найти добавочное давление внутри мыльного пузыря диаметром d=5 см. Какую работу нужно совершить, чтобы выдуть этот пузырь? 13. В сосуде находится сыворотка крови, плотность которой 1026 кг/м3 и α=6 ·10-2 Н/м. На глубине 25 см от поверхности жидкости образовался пузырек воздуха диаметром 10 мкм. Определить давление воздуха в пузырьке, если атмосферное давление равно 750 мм. рт. столба. 14. Какой объем крови протекает через кровеносный сосуд длиной 50 мм и диаметром 3 см за 1 минуту, если на его концах имеется разность давлений в 2 мм. рт. ст. (η=4 · 10-3 Па·с) Шарик всплывает с постоянной скоростью в жидкости, плотность которой в 4 раза больше плотности материала шарика. Во сколько раз сила трения, действующая на всплывающий шарик, больше веса этого шарика. 16. В сосуде с глицерином падает свинцовый шарик. Определить максимальное значение диаметра шарика, при которой движение слоев глицерина, вызванное падением шарика, является ещё ламинарным. Движение считать установившимся.(Rе кр=0,5, ρгл=1,26 · 103 кг/м3, ρсв =11,3 · 103 г/м3, η=1,48 Па·с) 17. Вода течет по круглой гладкой трубе диаметром d=5 см со средней по сечению скоростью <v>=10 см/с. Определить число Рейнольдса Re, для потока жидкости в трубе и указать характер течения жидкости. 18. По трубе течёт машинное масло. Максимальная скорость vmax, при которой движение масла в этой трубе остаётся ещё ламинарным, равно 3,2 см/с. При какой скорости v движение глицерина в этой же трубе переходит из ламинарного в турбулентное?(Re=2300, ρмм=0,9 кг/м3, ρгл=1260 кг/м3, ηмм=0,1 Па·с, ηгл=1,48 Па·с) 19. Стальной шарик диаметром 1 мм падаете постоянной скоростью v=0,185 см/с в большом сосуде, наполненном касторовым маслом. Найти динамическую вязкость касторового масла.( Rст=7870 кг/м3, Rкм=960 кг/м3) 20. Льдина площадью поперечного сечения S=1 м2 и высотой Н=0,4 м плавает в воде. Какую работу А надо совершить, чтобы полностью погрузить льдину в воду? Плотность воды ρв=1000 кг/м3, плотность льда ρл=900 кг/м3. 21. Найти добавочное давление р внутри мыльного пузыря диаметром d=10 см. Определить работу А, которую нужно совершить, чтобы выдуть этот пузырь. 22. Определить изменение свободной энергии ΔЕ поверхности мыльного пузыря при изотермическом увеличении его объема от V1=10 см3 до V2=2V1. 23. Воздушный пузырек диаметром d=2 мкм находится в воде у самой ее поверхности. Определить плотность ρ воздуха в пузырьке, если воздух над поверхностью воды находится при нормальных условиях. 24. Глицерин поднялся в капиллярной трубке на высоту h=20 мм. Определить поверхностное натяжение σ глицерина, если диаметр d канала трубки равен 1 мм. 25. Широкое колено U-образного ртутного манометра имеет диаметр d1=4 см, узкое d2=0,25 см. Разность Δh уровней ртути в обоих коленах равна 200 мм. Найти давление р, которое показывает манометр, приняв во внимание поправку на капиллярность. 26. В широкой части горизонтально расположенной трубы нефть течет со скоростью v1=2 м/с. Определить скорость v2 нефти в узкой части трубы, если разность Δр давлений в широкой и узкой частях ее равна 6,65 кПа. 27. К поршню спринцовки, расположенной горизонтально, приложена сила F=15 Н. Определить скорость v истечения воды из наконечника спринцовки, если площадь S поршня равна 12 см2. 28. Струя воды диаметром d=2 см, движущаяся со скоростью v=10 м/с, ударяется о неподвижную плоскую поверхность, поставленную перпендикулярно струе. Найти силу F давления струи на поверхность, считая, что после удара о поверхность скорость частиц воды равна нулю. 29. Бак высотой Н=2 м до краев заполнен жидкостью. На какой высоте h должно быть проделано отверстие в стенке бака, чтобы место падения струи, вытекающей из отверстия, было на максимальном от бака расстоянии? 30. Из бака водонапорной башни, расположенного на высоте h=10 м, вода по трубе поступает в кран, находящийся вблизи поверхности земли. За какое время τ кран наполнит ведро объемом V=10 л? Диаметр выходного отверстия крана d=1 см. Сопротивлением течению жидкости в трубе и кране пренебречь.
32. В подвале дома вода отопительной системы поступает в трубу диаметром d1=4 см со скоростью v1=0,5 м/с под давлением р1=3 атм. Каковы скорость течения v2 и давление в трубке р2 диаметром d2=2,6 см на втором этаже, расположенном на 5 м выше? 33. Определить скорость полета струи из шприца диаметром d=4 см, на поршень которого давит сила F=30 Н. Площадь отверстия шприца много меньше площади поршня, сопротивлением воздуха пренебречь. Плотность жидкости ρв=1000 кг/м3. 34. Цилиндр диаметром D заполнен водой и расположен горизонтально. С какой скоростью v перемещается в цилиндре поршень, если на него действует сила F, а из отверстия в дне цилиндра вытекает струя диаметром d? Силу тяжести не учитывать. Плотность жидкости ρ. 35. какой скоростью v вытекает вода из маленького отверстия в дне широкого цилиндрического бака в момент времени, когда он заполнен до высоты h? Какой объем воды Q нужно доливать в бак в единицу времени, чтобы уровень жидкости в баке остался неизменным? Площадь отверстия S. 36. Широкий сосуд с небольшим отверстием в дне наполнен водой и керосином. Пренебрегая вязкостью, найти скорость v вытекающей воды, если толщина слоя воды h1, а слоя керосина h2. Плотность воды ρ1, керосина – ρ2 (ρ1> ρ2). 37. На гладкой горизонтальной поверхности стоит сосуд с водой. В боковой стенке сосуда у дна имеется малое отверстие площадью S. Какую силу F нужно приложить к сосуду, чтобы удержать его в равновесии, если высота уровня воды в сосуде равна h? Плотность воды ρ. |
|
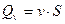


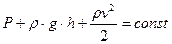









 31. Вода протекающая в широкой части горизонтальной трубы, имеет давление р=2 · 105 Па, в два раза больше атмосферного давления р0, и скорость v1=1 м/с (рис.). При каком соотношении диаметров D/d большой и малой трубы вода не будет вытекать из небольшого отверстия, расположенного в верхней части малой трубы?
31. Вода протекающая в широкой части горизонтальной трубы, имеет давление р=2 · 105 Па, в два раза больше атмосферного давления р0, и скорость v1=1 м/с (рис.). При каком соотношении диаметров D/d большой и малой трубы вода не будет вытекать из небольшого отверстия, расположенного в верхней части малой трубы?