|
|
Динамика вращательного движения.1. Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси:
где М – момент вращающей силы, действующий на тело в течение времени dt; J – момент инерции тела; ω – угловое ускорение. Или 2. Момент импульса вращающегося тела относительно оси:
3. Момент инерции материальной точки:
4. Теорема Штейнера:
где J0 – момент инерции тела, относительно оси, проходящей через центр тяжести тела параллельно заданной оси; d – расстояние между осями; m – масса тела. 5. Закон сохранения момента импульса тела:
6. Работа постоянного момента силы М, действующего на вращающееся тело:
где φ – угол поворота тела; [φ] = рад. 7. Мгновенная мощность, развиваемая при вращении тела
8. Кинетическая энергия вращающегося тела:
Задачи.
2. Вал в виде сплошного цилиндра массой m1=10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m2= 2 кг. С каким ускорением а будет опускаться гиря, если ее предоставить самой себе? 3. Платформа в виде диска радиусом R= 1,5 м и массой m1=180 кг вращается по инерции около вертикальной оси с частотой n=10 мин-1. В центре платформы стоит человек массой m2=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы. 4. Человек стоит в центре скамьи Жуковского и вместе с ней вращается по инерции. Частота вращения n1=0.5 c-1. Момент инерции J0 тела человека относительно оси вращения равен 1,6 кг·м2. В вытянутых в стороны руках человек держит по гире массой m=2 кг каждая. Расстояние между гирями l1=1.6 м. Определить частоту вращения n2 скамьи с человеком, когда он опустит руки и расстояние l2 между гирями станет равным 0,4 м. Моментом инерции пренебречь.
6. Два маленьких шарика массой m=10 г каждый скреплены тонким невесомым стержнем длиной l=20 см.Определить момент инерции J системы относительно оси, перпендикулярной стержню и проходящей через центр масс. 7. Определить момент инерции J тонкого однородного стержня длиной l=30 см и массой m=100 г относительно оси перпендикулярной стержню и проходящей через: 1) его конец; 2) его середину; 3) точку, отстоящую от конца стержня на 1/3 его длины. 8. Определить момент инерции J тонкого однородного стержня длиной l=60 см и массой m=100 г относительно оси, перпендикулярной стержню и проходящей через точку стержня, удаленную на а=20 см от одного из его концов. 9. Найти момент инерции J тонкого однородного кольца радиусом R=20 см и массой т=100 г относительно оси, лежащей в плоскости кольца и проходящей через его центр. 10. Определить момент инерции J кольца массой m=50 г и радиусом R=10 см относительно оси, касательной к кольцу. 11. Диаметр диска d=20 см, масса m=800 г. Определить момент инерции J диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. 12. Тонкий однородный стержень длиной l=50 см и массой m=400 г вращается с угловым ускорением ε=3 рад/с2 около оси, проходящей перпендикулярно стержню через его середину. Определить вращающий момент М. 13. На горизонтальную ось насажены маховик и легкий шкив радиусом R=5 см. На шкив намотан шнур, к которому привязан груз массой m=0,4 кг. Опускаясь равноускоренно, груз прошел путь s=1,8 м за время t=3 с. Определить момент инерции J маховика. Массу шкива считать пренебрежимо малой. 14. Вал массой m=100 кг и радиусом R=5 см вращался с частотой n=8 с-1. К цилиндрической поверхности прижали тормозную колодку с силой F=40 Н, под действием которой вал остановился через t=10 с. Определить коэффициент трения μ. 15. Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузики массой m1=100 г и m2=110 г. С каким ускорением а будут двигаться грузики, если масса m блока равна 400 г? Трение при вращении блока ничтожно мало. 16.Через неподвижный блок массой m=0,2 кг перекинут шнур, к концам которого подвесили грузы массами m1=0.3 кг и m2= 0,5 кг. Определить силы натяжения Т1 и Т2 шнура по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу. 17. Человек стоит на скамье Жуковского и ловит рукой мяч массой m=0,4 кг, летящий в горизонтальном направлении со скоростью v=20 м/с. Траектория мяча проходит на расстоянии r=0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью ω начнет вращаться скамья Жуковского с человеком, поймавшим мяч, если суммарный момент инерции J человека и скамьи равен 6 кг·м2? 18. На краю горизонтальной платформы, имеющей форму диска радиусом R=2 м, стоит человек массой т1=80 кг. Масса m2 платформы равна 240 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью ω будет вращаться платформа, если человек будет идти вдоль ее края со скоростью v=2 м/с относительно платформы. 19. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек массой т1=60 кг. На какой угол φ повернется платформа, если человек пойдет вдоль края платформы и, обойдя его, вернется в исходную точку на платформе? Масса т2 платформы равна 240 кг. Момент инерции J человека рассчитывать, как для материальной точки. 20. Платформа в виде диска радиусом R=1м вращается по инерции с частотой п1=6 мин-1. На краю платформы стоит человек, масса m которого равна 80 кг. С какой частотой п будет вращаться платформа, если человек перейдет в ее центр? Момент инерции J платформы равен 120кг·м2. Момент инерции человека рассчитывать, как для материальной точки. 21. В центре скамьи Жуковского стоит человек и держит в руках стержень длиной l=2,4 м и массой т=8 кг, расположенный вертикально по оси вращения скамьи. Скамья с человеком вращается с частотой n1=1с-1. С какой частотой п2 будет вращаться скамья с человеком, если он повернет стержень в горизонтальное положение? Суммарный момент инерции J человека и скамьи равен 6 кг·м2. 22. Человек стоит на скамье Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения скамьи. Стержень служит осью вращения колеса, расположенного на верхнем конце стержня. Скамья неподвижна, колесо вращается с частотой п=10 с-1. Радиус R колеса равен 20 см, его масса m=З кг. Определить частоту вращения п2 скамьи, если человек повернет стержень на угол 180°? Суммарный момент инерции J человека и скамьи равен 6 кг·м2. Массу колеса можно считать равномерно распределенной по ободу. 23. Шарик массой т=100 г, привязанный к концу нити длиной l1=1 м, вращается, опираясь на горизонтальную плоскость, с частотой n1=1 c-1. Нить укорачивается и шарик приближается к оси вращения до расстояния l2=0,5 м. С какой частотой n2 будет при этом вращаться шарик? Какую работу А совершит внешняя сила, укорачивающая нить? Трением шарика о плоскость пренебречь. 24. Маховик вращается по закону, выраженному уравнением φ=А+Вt+Сt2, где А=2 рад, В=32 рад/с, С= -4 рад/с2. Найти среднюю мощность (N), развиваемую силами, действующими на маховик при его вращении, до остановки, если его момент инерции J=100 кг·м2. 25. Маховик вращается по закону, выраженному уравнением φ=А+Вt+Ct2, где А=2 рад, В=16 рад/с, С= -2 рад/с2. Момент инерции J маховика равен 50кг·м2. Найти законы, по которым меняются вращающий момент М и мощность N. Чему равна мощность в момент времени t=3 с? 26. Якорь двигателя вращается с частотой n=1500 мин-1. Определить вращающий момент М, если двигатель развивает мощность N=500 Вт. 27. Со шкива диаметром d=0,48 м через ремень передается мощность N=9 кВт. Шкив вращается с частотой n=240 мин-1. Сила натяжения Т1 ведущей ветви ремня в два раза больше силы натяжения T2 ведомой ветви. Найти силы натяжения обеих ветвей ремня. 28. Для определения мощности двигателя на его шкив диаметром d=20 см накинули ленту. К одному концу ленты прикреплен динамометр, к другому подвесили груз. Найти мощность N двигателя, вращающего с частотой n=24 с-1. Масса m груза равна 1кг и показание динамометра F=24 Н. 29. Маховик в виде диска массой т=80 кг и радиусом R=30 см находится в состоянии покоя. Какую работу А1 нужно совершить, чтобы сообщить маховику частоту n=10 с-1? Какую работу А2 пришлось бы совершить, если бы при той же массе диск имел меньшую толщину, но вдвое больший радиус? 30. Кинетическая энергия T вращающегося маховика равна 1 кДж. Под действием постоянного тормозящего момента маховик начал вращаться равнозамедленно и, сделав N=80 оборотов, остановился. Определить момент М силы торможения. 31. Маховик, момент инерции J которого равен 40 кг·м2, начал вращаться равноускоренно из состояния покоя под действием момента силы М=20 Н·м. Вращение продолжалось в течение t=10 с. Определить кинетическую энергию T, приобретенную маховиком. 32. Пуля массой т=10 г летит со скоростью v=800 м/с, вращаясь около продольной оси с частотой n=3000 с-1. Принимая пулю за цилиндрик диаметром d=8 мм, определить полную кинетическую энергию Т пули. 33. Сплошной цилиндр массой т=4 кг катится без скольжения до горизонтальной поверхности. Линейная скорость v оси цилиндра равна 1 м/с. Определить полную кинетическую энергию Т цилиндра. 34. К ободу однородного диска радиусом R =0.2 м приложена касательная сила Fk=98.1 Н. При вращении на диск действует момент сил трений Мтр= 4.9 Н·м. Найти массу m диска, если известно, что диск вращается с угловым ускорением β=100 рад/с. 35. К ободу колеса радиусом R=0.5 м и массой m=50 кг приложена касательная сила Fk=98,1 Н. Найти угловое ускорение β колеса. Через какое время t после начала действия силы колесо будет иметь частоту вращения υ=100 об/с? Колесо считать однородным диском. Трением пренебречь. 36. Блок массой m=1 кг укреплен на конце стола. Гири 1 и 2 одинаковой массы m1=m2=1кг соединены нитью и перекинуты через блок. Коэффициент трения гири 2 о стол k=0,1. Найти ускорение a с которым движутся гири, силы натяжения Т1 и Т2 нитей. Блок считать однородным диском. Трением в блоке пренебречь. 37. Вентилятор вращается с частотой υ=900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N= 75 об. Работа сил торможения А=44.4 Дж. Найти момент инерции J вентилятора и момент сил торможения М. 38. Горизонтальная платформа массой m1=100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой υ=10 об/мин. Человек массой m2=60 кг стоит при этом на краю платформы. С какой частотой υ2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека - точечной массой. 39. Однородный диск радиусом R=0.2 м и массой m=5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости ω вращения диска от времени t дается уравнением ω=Bt, где В=8 рад/с2. Найти касательную силу приложенную к ободу диска. Трением пренебречь. 40. Маховое колесо, момент инерции которого J=245 кг/м2, вращается с частотой υ=20 Гц/с. Через время t=1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. 41. На барабан радиусом R=20 см, момент инерции которого J=0.1 кг/м2, намотан шнур, к концу которого привязан груз массой т=0.5 кг. До начала вращения барабана высота груза над полом h1=1 м. Через какое время t груз опуститься до пола? Найти кинетическую энергию Wk груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь. 42. Шар массой m=1 кг, катящийся без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку v=10 см/с, а после - v=8 см/с. Найти количество теплоты Q, выделившейся при ударе о стенку. 43. Найти линейные скорости v движения центров масс шара, диска и обруча скатывающихся без скольжения с наклонной плоскости. Высота наклонной плоскости h=0.5 м, начальная скорость всех тел v0=0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения. 44. Шар радиусом R=10 см и массой m=5 кг вращается вокруг оси симметрии согласно уравнению φ=A+Bt2+Ct3 (В = 2 рад/с2, С = -0,5 рад/с3). Определить момент сил М для t=3 с. 45. Маховик в виде сплошного диска, момент инерции которого J=150 кг м2, вращается с частотой υ=240 об/мин. Через время t=1 мин действия на маховик момента сил торможения он остановился. Определить: 1) момент М сил торможения; 2) число оборотов маховика от начала торможения до полной остановки.
47. На однородный сплошной цилиндрический вал радиусом R=5 см и массой М=10 кг намотана легкая нить, к концу которой прикреплен груз массой т=1 кг (рис). Определить: 1) зависимость l(t), согласно которой движется груз; 2) силу натяжения нити Т; 3) зависимость φ(t), согласно которой прощается вал; 4) угловую скорость вала через t=1 с после начала движения; 5) тангенциальное (аτ) и нормальное (аn) ускорения точек, находящихся на поверхности вала.
49. С какой силой следует прижать тормозную колодку к колесу, вращающемуся с частотой n1=30 об/с, для его остановки в течение t=20 с, если масса колеса распределена по ободу и равна m=10 кг, диаметр колеса d=20 см? Коэффициент трения между колодкой и ободом колеса μ=0,5. 50. По ободу шкива, насаженного на общую ось с маховым колесом, намотана на нить, к концу которой подвешен груз массой 1 кг. На какое расстояние должен опуститься груз, чтобы колесо со шкивом получило скорость, соответствующую 60 об/мин? Момент инерции колеса со шкивом равен 0,42 кг·м2, радиус шкива равен 10 см. 51. Человек стоит на горизонтальной платформе и ловит рукой мяч массой m=0,4 кг, летящий в горизонтальном направлении со скоростью v=0,8 м от вертикальной оси вращения платформы. С какой угловой скоростью ω начнет вращаться платформа с человеком, поймавшим мяч? Суммарный момент инерции платформы и человека J=6 кг·м2. Горизонтальная платформа, имеющая форму эллипса радиусом 4 м, вращалась вокруг вертикальной оси, делая 4 об/мин. На платформе, на расстоянии 3 м от ее центра, стоял человек массой 60 кг. После того, как человек побежал по платформе в сторону ее первоначального вращения по окружности радиусом 3 м со скоростью 16,6 км/ч, платформа стала вращаться в обратном направлении, делая 3 об/мин. Определить массу платформы. Момент инерции человека рассчитывать как для материальной точки. 53. В центре горизонтальной платформы стоит человек и держит в руках тонкий стержень, расположенный вертикально по оси вращения платформы. Платформа с человеком вращается по инерции, делая n=1 об/с. С какой угловой скоростью ω будет вращаться платформа с человеком, если повернуть стержень в горизонтальное положение так, чтобы центр массы лежал на оси вращения. Суммарный момент инерции человека и платформы J=6 кг·м2. Длина стержня l=2,4 м, его масса m=8 кг. Платформа, имеющая форму сплошного однородного диска может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определить, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы. Человек массой 60 кг находится на неподвижной платформе массой 100 кг. Какой будет частота вращения платформы. если человек будет двигаться по окружности радиусом 5 м вокруг оси равна 4 км/ч. Радиус платформы 10 м. Считать платформу однородным диском, а человека – точечной массой. 56. Платформа, имеющая форму диска, может вращаться вокруг вертикальной оси. На краю платформы стоит человек. Человек начинает равномерно идти по краю платформы. На какой угол φ1 повернется платформа, когда человек возвратиться в исходную точку? Масса платформы m1=240 кг, масса человека m2=60 кг. Момент инерции человека рассчитывается как для материальной точки. Человек, стоящий в центре горизонтальной платформы, держит в расставленных руках гири. Платформа вращается с угловой скоростью, соответствующей 20 об/мин. Масса платформы 80 кг, диаметр платформы 2 м. После того, как человек опустил руки, уменьшив свой момент инерции в 3 раза, число оборотов платформы в еденицу времени возросло до 21 об/мин. Определить начальный момент инерции человека. Платформу считать однородным диском. Работа. Мощность. Энергия. Работа, совершаемая силой:
где α – угол между направлениям векторов силы F и перемещения S. Работа, совершаемая переменной силой:
Мгновенная мощность:
где dA – работа совершаемая за промежуток времени dt.
Кинетическая энергия материальной точки:
где р – импульс точки. Потенциальная энергия тела и сила, действующая на тело в данной точке поля, связаны соотношением:
Потенциальная энергия упруго деформированного тела (сжатой или растянутой пружины):
Потенциальная энергия гравитационного взаимодействия двух материальных точек (или тел) массами m1 и m2, находящихся на расстоянии r друг от друга:
Потенциальная энергия тела, находящегося в однородном поле силы тяжести:
Закон сохранения энергии в механике выполняется в замкнутой системе и записывается в виде:
Скорости абсолютно неупругих тел после удара:
Скорости абсолютно упругих тел после удара:
Задачи. 1. Определить ускорение, с которым цилиндрическая бочка массой М, целиком заполненная массой m, скатывается без скольжения с наклонной плоскости с углом α. Трением между жидкостью и бочкой и моментами инерции днищ бочки пренебречь. 2. С какой скоростью двигался вагон массой 20 т, если при ударе о стенку каждый буфер сжался на 10 см? Известно, что пружина каждого сжимается на 1 см под действием силы 104 Н. 3. К стальной проволоке длинной 10 м и диаметром 2 мм подвешивают груз массой 100 кг. Найти изменение объема проволоки и энергию упругой деформации. Модуль Юнга 1,96 · 1011 Н/м2, коэффициент Пуассона 0,3. 4. Под действием постоянной силы F вагонетка прошла путь S=5м и приобрела скорость v=2 м/с. Определить работу А силы, если масса вагонетки m=400 кг и коэффициент трения k=0,01. 5. Трактор за время t=8 час вспахивает поле площадью S=2 га при захвате лемехов l=1,2 м и сопротивлении почвы Fтр=17 640 Н. Определить N мощность двигателя трактора, если его коэффициент полезного действия η=80%. 6. Определить мощность электродвигателя, если его якорь вращается с частотой n=2,5 с-1, а момент силы равен М=14 H·м. 7. Совершив работу, равную А=20 Дж, удаётся сжать пружину на 2 см. Определить работу, которую надо выполнить, чтобы сжать пружину на 4 см. 8. Груз массой m=5 кг падает с высоты Н=5 м и проникает в грунт на глубину L=5 см. Определить среднюю силу сопротивления грунта. 9. Для подъёма зерна на высоту Н=10 м установили транспортёр мощностью N=4 кВ. Определить массу зерна, поднятого за время t=8 час работы транспортёра. Коэффициент полезного действия установки принято равным η=13,6%. 10. Тело массой m1=0,5 кг надает с некоторой высоты на плиту массой m2=1 кг, укреплённую па пружине жёсткостью k=4 кН/м. Определить, на какую длину сожмётся пружина, если в момент удара скорость грузи v=5 м/с. Удар считать неупругим. 11. Шар массой m1=2 кг, движущийся со скоростью v1=1,2 м/с, налетает на покоящийся шар массой m2=1,5 кг. Вычислить скорости шаров после упругого взаимодействия. 12. Баба копра массой m1=500 кг падает на сваю массой m2=100 кг со скоростью v1=4 м/с. Определить: 1) Кинетическую энергию W1 копра в момент удара. 2) Энергию W2, затрачиваемую на деформацию сваи. 3) Энергию W3, затрачиваемую на углубление сван в груш. 4) Коэффициент полезного действия η удара копра о сваю. 13. Спутник массой m=3 т вращается вокруг Земли по круговой орбите на высоте h=520 км. Определить полную механическую энергию спутника относительно Земли. |
|

 , где β – угловое ускорение.
, где β – угловое ускорение.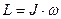



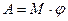


 5. Стержень длинной l=1,5 м и массой М=10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня (рис.). В середину стержня ударяет пуля массой m=10 г, летящая в горизонтальном направлении со скоростью v0=500 м/с, и застревает в стержне. На какой угол φ после удара отклонится стержень?
5. Стержень длинной l=1,5 м и массой М=10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня (рис.). В середину стержня ударяет пуля массой m=10 г, летящая в горизонтальном направлении со скоростью v0=500 м/с, и застревает в стержне. На какой угол φ после удара отклонится стержень? 46. К ободу однородного сплошного диска радиусом R=0,5 м приложена постоянная касательная сила F=100 Н. При вращении диска на него действует момент сил трения Мтр=2 Н·м. Определить массу т диска, если известно, что его угловое ускорение α постоянно и равно 16 рад/с2.
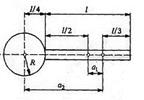
46. К ободу однородного сплошного диска радиусом R=0,5 м приложена постоянная касательная сила F=100 Н. При вращении диска на него действует момент сил трения Мтр=2 Н·м. Определить массу т диска, если известно, что его угловое ускорение α постоянно и равно 16 рад/с2. 48. На ступенчатый блок, радиусы которого r1=0,3 м и г2=10 см, намотаны в противоположных направлениях нити (рис). К концам нитей привязаны грузы массами m1=m2=1 кг. Момент инерции блока J=0,3 кг·м2. Пренебрегая силой трения и массой нитей, определить ускорения грузов и натяжение каждой нити.
48. На ступенчатый блок, радиусы которого r1=0,3 м и г2=10 см, намотаны в противоположных направлениях нити (рис). К концам нитей привязаны грузы массами m1=m2=1 кг. Момент инерции блока J=0,3 кг·м2. Пренебрегая силой трения и массой нитей, определить ускорения грузов и натяжение каждой нити.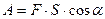




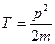
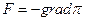 или
или 






